陕西省镇安中学2016届高三数学上学期第二次月考试题文VIP免费

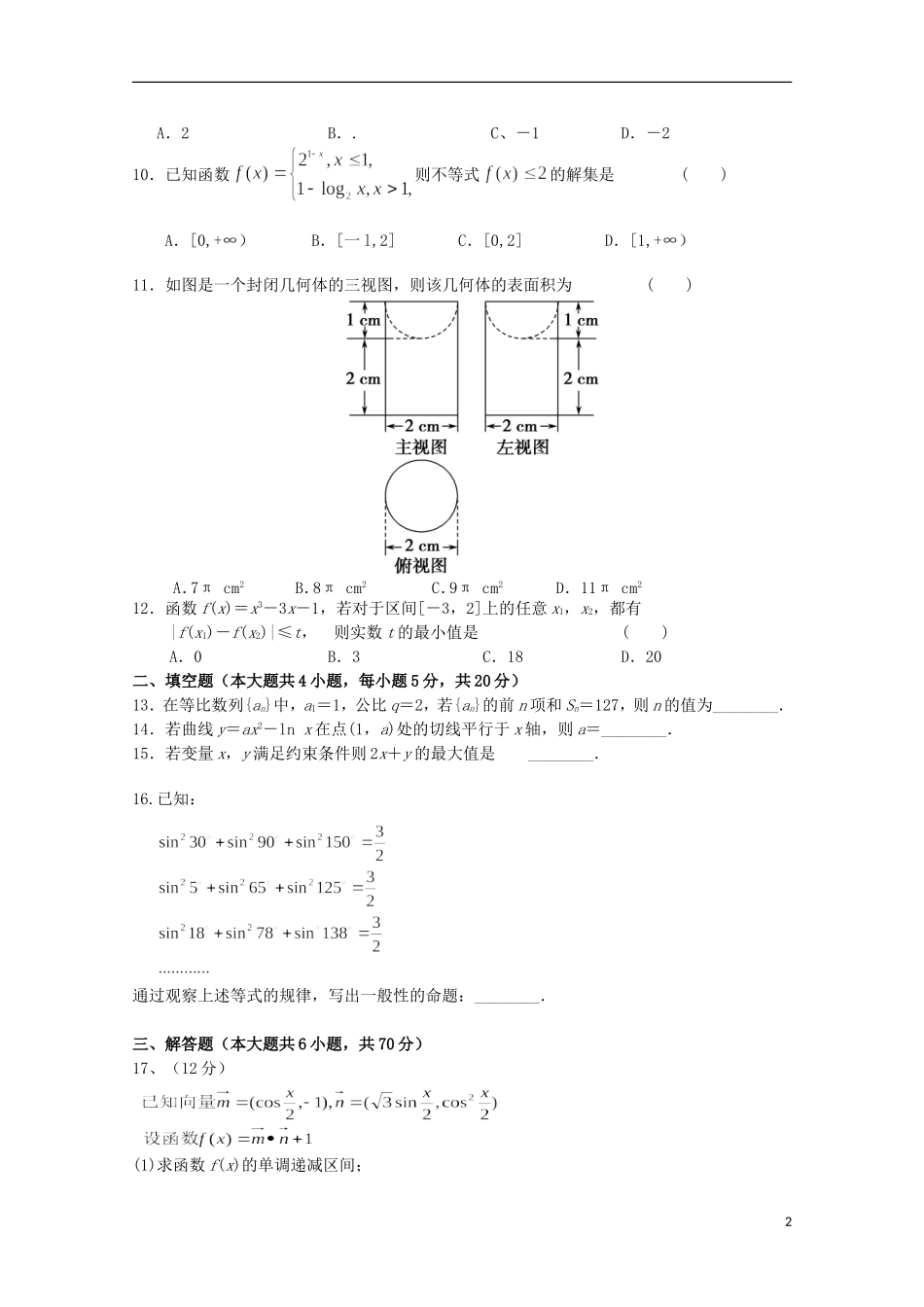
镇安中学2016届高三第二次月考数学（文）试题一、单项选择题（本大题共12小题，每小题5分，共60分）1．集合{|lg0}Mxx，2{|4}Nxx，则MN（）A．(12)，B．[12)，C．(12]，D．[12]，2．已知向量a＝(－1，2)，b＝(3，m)，m∈R，则“m＝－6”是“a∥(a＋b)”的()A．充要条件B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件3．复数z满足(1＋i)z＝2i，则复数z在复平面内对应的点在()A．第一象限B．第二象限C．第三象限D．第四象限4．已知x，y之间的数据如下表所示，则回归直线过点()x12345y1.21.82.53.23.8A.(0，0)B．(2，1.8)C．(3，2.5)D．(4，3.2)5．已知抛物线y2＝2px(p＞0)的准线与曲线x2＋y2－4x－5＝0相切，则p的值为()A．B．C.1D.26．，则＝()A.-1B．1C.-2D．27．以Sn表示等差数列{an}的前n项和，若a2＋a7－a5＝6，则S7＝()A．42B．28C．21D．148．函数f(x)＝2sin(ωx＋φ)(ω>0，－<φ<)的部分图像如图所示，则ω，φ的值分别是()A．2，－B．2，－C．4，－D．4，9．执行如图所示的算法框图，输出的M值是()1A．2B．.C、－1D．－210．已知函数则不等式的解集是()A．[0,+∞）B．[一l,2]C．[0,2]D．[1,+∞）11．如图是一个封闭几何体的三视图，则该几何体的表面积为()A．7πcm2B．8πcm2C．9πcm2D．11πcm212．函数f(x)＝x3－3x－1，若对于区间[－3，2]上的任意x1，x2，都有|f(x1)－f(x2)|≤t，则实数t的最小值是()A．0B．3C．18D．20二、填空题（本大题共4小题，每小题5分，共20分）13．在等比数列{an}中，a1＝1，公比q＝2，若{an}的前n项和Sn＝127，则n的值为________．14．若曲线y＝ax2－lnx在点(1，a)处的切线平行于x轴，则a＝________．15．若变量x，y满足约束条件则2x＋y的最大值是________．16.已知：通过观察上述等式的规律，写出一般性的命题：________．三、解答题（本大题共6小题，共70分）17、（12分）(1)求函数f(x)的单调递减区间；2(2)在△ABC中，角A，B，C的对边分别为a，b，c，且满足a2＋b2＝6abcosC，sin2C＝2sinAsinB，求的值．18、（12分）19、（10分）如图所示，在三棱锥A－BOC中，OA⊥底面BOC，∠OAB＝∠OAC＝30°，AB＝AC＝4，BC＝2，动点D在线段AB上．（1）求证：平面COD⊥平面AOB；（2）当OD⊥AB时，求三棱锥C－OBD的体积．20、（12分）某校高三年级一次数学考试之后，为了解学生的数学学习情况，随机抽取n名学生的数学成绩，制成如表所示的频率分布表.组号分组频数频率第一组[90，100)50.05第二组[100，110)a0.35第三组[110，120)300.30第四组[120，130)20b第五组[130，140)100.10合计n1.00(1)求a，b，n的值；(2)若从第三、四、五组中用分层抽样方法抽取6名学生，并在这6名学生中随机抽取2名与张老师面谈，求第三组中至少有1名学生与张老师面谈的概率．21、（12分）已知椭圆C：＋＝1(a＞b＞0)的离心率为，椭圆C的长轴长为4.(1)求椭圆C的方程；(2)已知直线l：y＝kx＋与椭圆C交于A，B两点，是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O？若存在，求出k的值；若不存在，请说明理由．22、（12分）设函数.21ln2bxaxxxf(1)当21ba时，求函数xf的单调区间；3(3)当1,0ba时，方程mxxf在区间2,1e内有唯一实数解，求实数m的取值范围。4数学（文）参考答案一、选择题：CAACDDABCACD二、填空题：13、7.14、15、7三、解答题：17、（12分）解：(1)f(x)＝sin·cos－cos2＋1＝sinx－cosx＋＝(2)由a2＋b2＝6abcosC，sin2C＝2sinAsinB⇒c2＝2ab，∴cosC＝＝＝3cosC－1，即cosC＝，又 0＜C＜π，C＝，∴18、（12分）519、（10分）解:(1)证明： AO⊥底面BOC，∴AO⊥OC，AO⊥OB． ∠OAB＝∠OAC＝30°，AB＝AC＝4，∴OC＝OB＝2.又BC＝2，∴OC⊥OB，∴OC⊥平面AOB． OC在平面COD内.∴平面COD⊥平面AOB．(2)解： OD⊥AB，∴BD＝1，OD＝.∴VC－OBD＝×××1×2＝.20、（12分）解(1)依题意，得＝0.05，＝0.35，＝b，解得n＝100，a＝35，b＝0.2.(2)因为第三、四、五组共有60名学生，用分层抽样方法抽取6名学生，则第三、四、五组分别抽取×6＝3(名)，×6＝2(名)，×6＝1(名)．第三组的3名学生记为a1，a2，a3，...