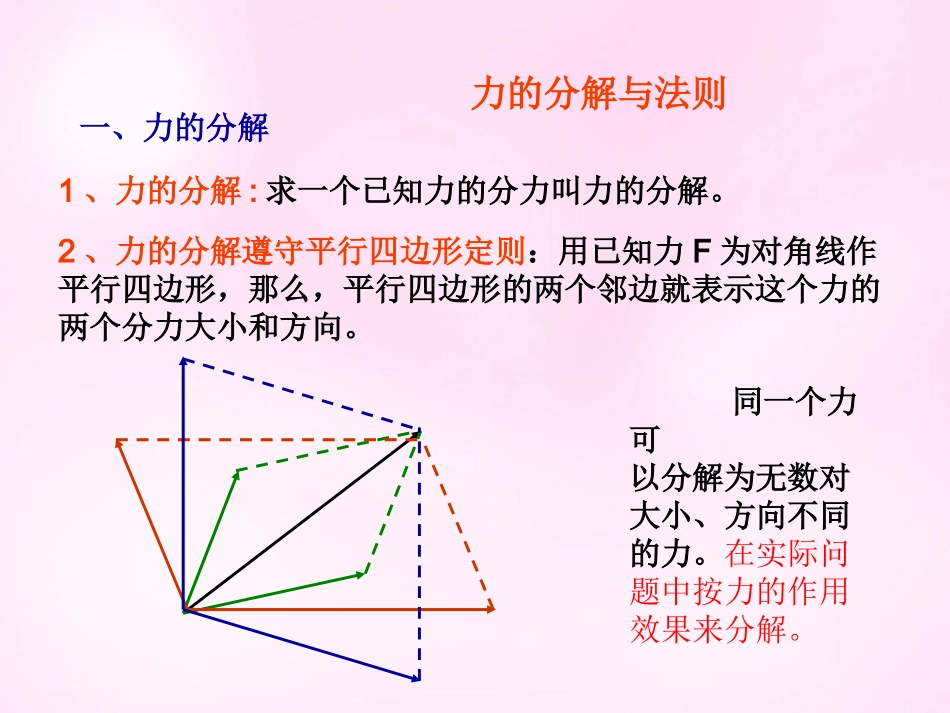
力的分解拖拉机拉着耙,对耙斜向上的拉力F产生两个效果,一个水平的力F1使耙前进,一个竖直向上的力F2把耙向上提。可见力F可以用两个力F1和F2来代替。力F1和F2是力F的分力。求一个已知力的分力叫做力的分解。力的分解是力的合成的逆运算,同样遵守平行四边形定则。1、力的分解:求一个已知力的分力叫力的分解。力的分解与法则2、力的分解遵守平行四边形定则:用已知力F为对角线作平行四边形,那么,平行四边形的两个邻边就表示这个力的两个分力大小和方向。同一个力可以分解为无数对大小、方向不同的力。在实际问题中按力的作用效果来分解。一、力的分解3、一个已知力分解时,有无数对可能分力4、力的效果分解:由力的效果来确定分力方向的分解方法叫效果分解力的分解举例思考:重力如何效果分解呢?在进行力的效果分解时,一般先根据力的作用效果根据力的作用效果来确定分力的方向方向,再根据平行四边形法则来计算分力的大小。力的作用效果如何体现呢?例1、重为G的物体静止在倾角为θ的斜面上,求:物体受到的弹力和摩擦力大小?θ力的分解举例GG1=GsinθG2=GcosθθθFN=G2=Gcosθf=G1=Gsinθ思考题:当斜面倾斜角增大时,分析:G1和G2如何变化?2、当倾斜角减小时,分析G1和G2如何变化?FNf解:据二力平衡条件有:将重力按效果方向分解为G1和G2力的分解举例GFNG1例2、重为G的球放在光滑的竖直挡板和倾角为的斜面之间,求挡板和斜面对球的作用力各多大?解:对球受力分析F=G1=GtanN=G2=G/cosG2把重力按效果分解为G1和G2,则有:思考:可以用合成法解此题吗?力的正交分解•在很多问题中,常把各个力分解为互相垂直的两个方向,特别是物体受多个力作用时,把物体受到的各个力都分解到互相垂直的两个方向上去,先分别求出两个垂直方向上的力的合力,然后再求出总的合力,这样可把复杂问题简化,这种方法叫正交分解法.1、定义:把一个物体受到的各个力都分解到两个互相垂直的方向,这种分解方法叫正交分解法二、力的正交分解2、建立坐标的原则:尽可能让更多的力落在X轴、Y轴上3、正交分解步骤:①建立xoy直角坐标系②沿x、y轴将各力分解并标示各分力③求xy轴上的合力Fx,Fy④最后求Fx和Fy的合力Fxy大小:22yxFFF方向:xyFFtanF1F2F3OF2yF1yF3yF3xF1xF2X怎样去选取坐标呢?原则上是任意的,实际问题中,让尽可能多的力落在这个方向上,这样就可以尽可能少分解力.例3:物体受到三个共点力F1=20N,F2=10N、F3=30N(方向如图)作用,求物体分别沿水平方向和竖直方向受到的合力。xy37o53ooF2F3F1FX=F1cos37O+(-F2cos53O)=20×0.8N-10×0.6N=10NFY=F1sin37O+F2sin53O+(-F3)=20×0.6N+10×0.8N-30N=-10N力的正交分解F1xF2xF1yF2y22221010102FFxFyN解:将F1和F2和F3沿水平方向和竖直方向分解:tanθ=Fy/Fx=1所以θ=450例4、重量为40N的物体与竖直墙壁间的动摩擦因数μ=0.4,若用斜向上的推力F=50N压住物体,物体处于静止状态,如图所示,这时物体受到的摩擦力是N,要使物体匀速下滑,推力F大小应为N.平衡问题尽可能让更多的力在X轴、Y轴上列方程:FX=0、FY=0把不在轴上的力进行分解力的正交分解在平衡问题中的应用GfNF解(1)物体静止时,对物体受力分析,xyFxFyFx合Fy合=0=0FxFy=N+f=G370=N+f=GFcos370Fsin370即即f=G-Fsin370=40N-50×0.6N=10N将F=50N,代入②得②①力的正交分解将F分解到坐标轴上,并建立坐标系,则有:Gf'N'F'(2)匀速下滑时,对物体受力分析,xyF'xF'yF'xF'y=N'+f'=G370=N'+f'=GF'cos370F'sin370即④③⑤又有:f'=µN'联立③④⑤得:F'sin370+µF'cos370=GF'=sin370+µcos370G=0.6+0.4×0.840N=43.5N力的正交分解将F'分解到坐标轴上,并建立坐标系,则有:力的分解举例作业:竖直墙上挂一个重为10N的光滑球,细绳与竖直方向成θ=300角,求:球受到绳子的拉力和墙的支持力大小。θ解:(合成法)解:(正交分解法)注意:两种解法要分别画受力图力的分解唯一性条件三、已知力分解的唯一性条件1、已知两个分力的方向,分解是唯一的。FF1F22、已知一个分力的大小和方向,有唯一解。F1F2F力的分解唯一性条件3、已知一个分力F1的方向和另...