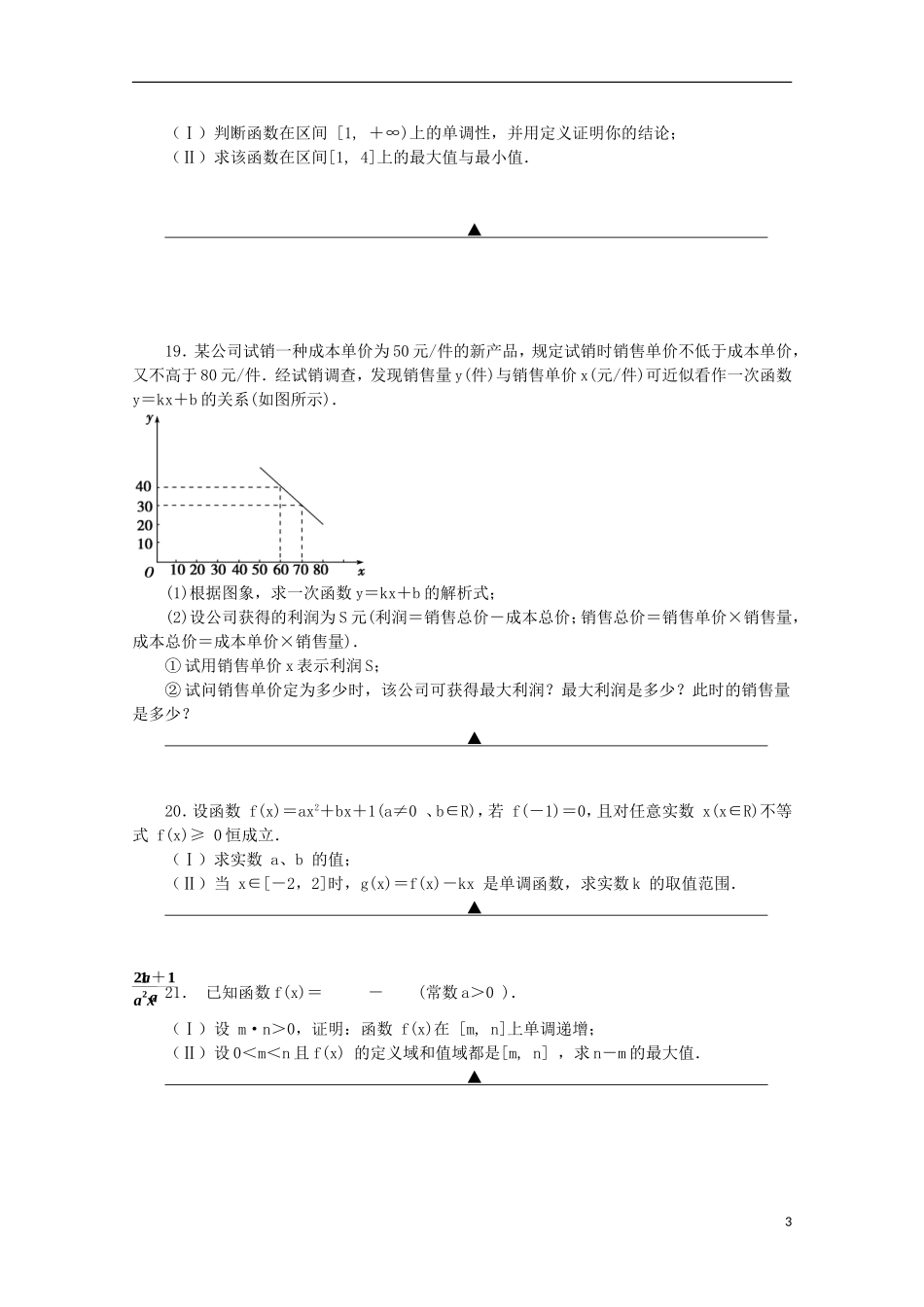
1x2x23-x2-12121212x2x2xx21-x1-1x2x2122x3x1-x1-3x1+x1-2x1x2x1x2323232323232四川省彭州中学2015级10月考试数学试题注意事项:1、答题前,务必将自己的姓名、准考证号、班级填写在答题卡规定位置上。2、答选择题时,必须使用2B铅笔将机读卡上对应题目的答案标号涂黒,如需改动,用像皮擦干净后,再选涂其它答案标号。3、答非选择题时,必须用0.5毫米黑色签字笔,将答案书写在答题卡规定位置上。4、所有题目必须在答案卡上作答,在试卷上答题无效。5、考试结束后,请将机读卡和答题卡一并交回。一、选择题(每题5分,共60分)1.设集合M={m∈Z|-3<m<2},N={n∈Z|-1≤n≤3},M∩N=A.[0,1}B.{-1,0,1}C.{0,1,2}D.{-1,0,1,2}2.函数y=的定义域为A.(-∞,1]B.(-∞,2]C.(-∞,)∪(,1)D.(-∞,-)∪(-,1]3.下列各组函数表示同一函数的是A.f(x)=,g(x)=|x|B.f(x)=1,g(x)=x0C.f(x)=,g(x)=()2D.f(x)=x+1,g(x)=4.下列函数是偶函数的是:A.y=xB.y=x3C.y=2x2-3D.y=x2,x∈[0,1]5.满足条件{1,2,3}M{1,2,3,4,5,6}的集合M的个数是A.8B.7C.6D.56.已知g(x)=1-2x,f(g(x))=,则f()=A.1B.3C.30D.157.已知f(+1)=x+3,则f(x)的解析式可取A.B.C.D.-8.设全集为R,A={x|x<3或x>5},B={x|-3<x<3},则A.CR(A∪B)=RB.A∪(CRB)=RC.(CRA)∪(CRB)=RD.A∪B=R9.若f(x)是偶函数,其定义域为(-∞,+∞),且在[0,+∞)是减函数,则f(-)与f(-a2-)的大小关系是A.f(-)≥f(-a2-)B.f(-)<f(-a2-)132323232-x24+x2C(A)C(B)C(A)C(B)C(B)C(A)C(A)C(B)g(x)f(x)g(x)f(x)f(x)g(x)77a1+x1-2x1+x1+C.f(-)>f(-a2-)D.f(-)≤f(-a2-)10.函数y=2-的值域是A.[-2,2]B.[1,2]C.[0,2]D.[-,]11.用C(A)表示非空集合A中的元素个数,定义A*B=已知A={1,2},B={x|(x2+ax)(x2+ax+2)=0}且A*B=1,设实数a的所有取值构成集合S,则C(S)=A.4B.3C.2D.112.已知f(x)=3-2|x|,g(x)=x2-2x,F(x)=,则F(x)A.最大值为3,最小值为-1B.最大值为7-2,无最小值C.最大值为2-,无最小值D.既无最大值,又无最小值二、填空题(每题5分,共20分)13.已知集合A中含有两个元素1,-2,集合B={x|x2+ax+b=0},且A=B,则a=▲。14.函数y=|x|的单调减区间是▲。15.设f(x)是R上的奇函数,且当x<0时,f(x)=x2-3x+1,那么f(x)=▲.16.对于函数f(x)=(其中a为实数,x≠1),给出下列命题:①当a=1时,f(x)在定义域上为单调增函数;②f(x)的图像关于点(1,a)对称;③对任意a∈R,f(x)都不是奇函数;④当a=-1时,f(x)为偶函数;⑤当a=2时,对于满足条件2<x1<x2的所有x1,x2总有f(x1)-f(x2)<3(x2-x1).其中正确命题的序号为▲.三、解答题17.已知集合A={x|2≤x<7},B={x|3<x<10},(1)求A∪B(2)(RA)∩B▲18.已知函数f(x)=;22a1+a1a2x(Ⅰ)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论;(Ⅱ)求该函数在区间[1,4]上的最大值与最小值.▲19.某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).(1)根据图象,求一次函数y=kx+b的解析式;(2)设公司获得的利润为S元(利润=销售总价-成本总价;销售总价=销售单价×销售量,成本总价=成本单价×销售量).①试用销售单价x表示利润S;②试问销售单价定为多少时,该公司可获得最大利润?最大利润是多少?此时的销售量是多少?▲20.设函数f(x)=ax2+bx+1(a≠0、b∈R),若f(-1)=0,且对任意实数x(x∈R)不等式f(x)≥0恒成立.(Ⅰ)求实数a、b的值;(Ⅱ)当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.▲21.已知函数f(x)=-(常数a>0).(Ⅰ)设m·n>0,证明:函数f(x)在[m,n]上单调递增;(Ⅱ)设0<m<n且f(x)的定义域和值域都是[m,n],求n-m的最大值.▲3