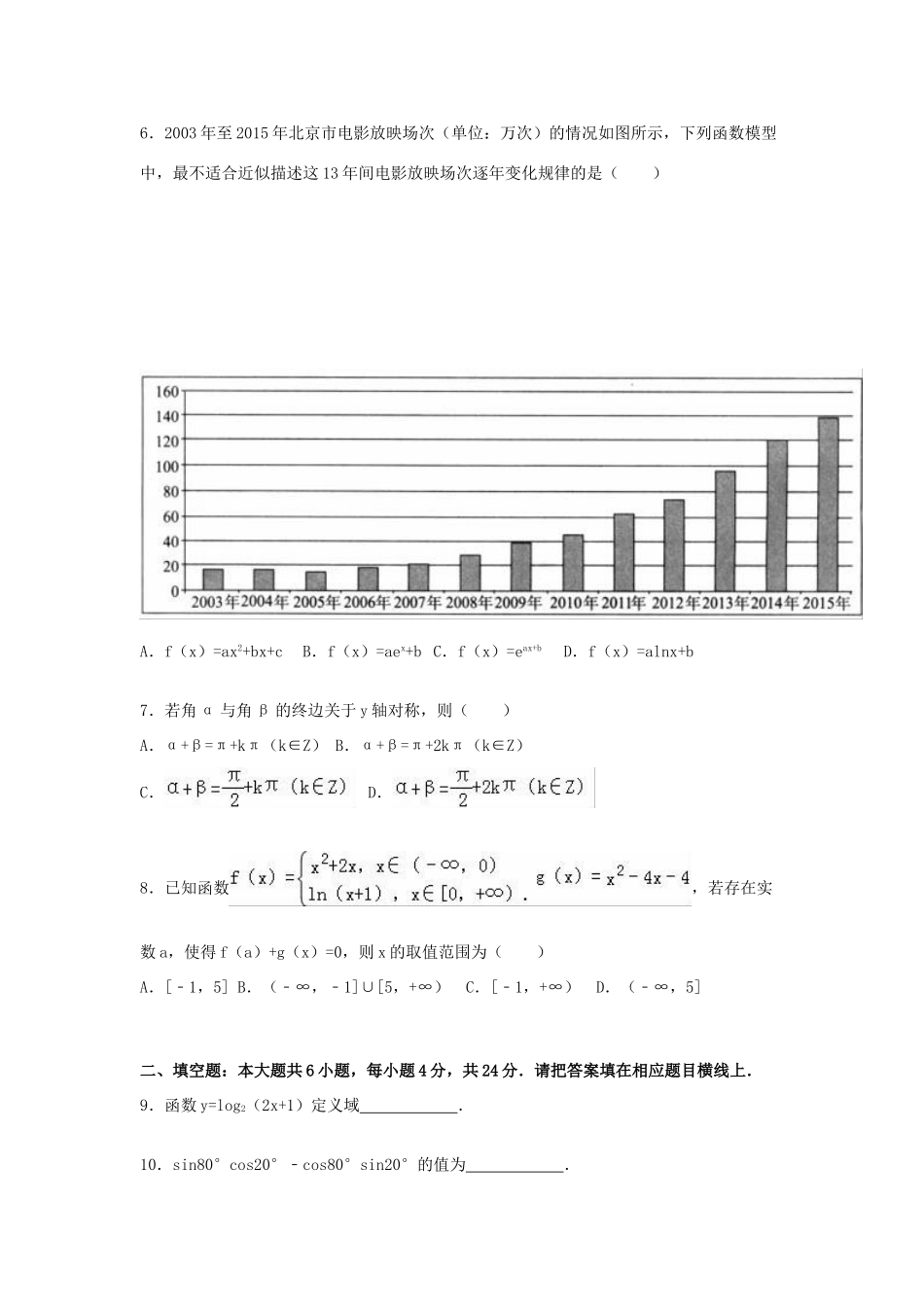
2015-2016学年北京市东城区高一(上)期末数学试卷一、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,选出符合题目要求的一项并填在答题卡中.1.已知集合A={0,1,2},B={2,3},则集合A∪B=()A.{1,2,3}B.{0,1,2,3}C.{2}D.{0,1,3}2.若角α的终边经过点P(1,﹣2),则tanα的值为()A.B.C.﹣2D.3.正弦函数f(x)=sinx图象的一条对称轴是()A.x=0B.C.D.x=π4.下列函数中,既是偶函数又存在零点的是()A.f(x)=sinxB.f(x)=x2+1C.f(x)=lnxD.f(x)=cosx5.函数f(x)=的大致图象是()A.B.C.D.6.2003年至2015年北京市电影放映场次(单位:万次)的情况如图所示,下列函数模型中,最不适合近似描述这13年间电影放映场次逐年变化规律的是()A.f(x)=ax2+bx+cB.f(x)=aex+bC.f(x)=eax+bD.f(x)=alnx+b7.若角α与角β的终边关于y轴对称,则()A.α+β=π+kπ(k∈Z)B.α+β=π+2kπ(k∈Z)C.D.8.已知函数,若存在实数a,使得f(a)+g(x)=0,则x的取值范围为()A.[﹣1,5]B.(﹣∞,﹣1]∪[5,+∞)C.[﹣1,+∞)D.(﹣∞,5]二、填空题:本大题共6小题,每小题4分,共24分.请把答案填在相应题目横线上.9.函数y=log2(2x+1)定义域.10.sin80°cos20°﹣cos80°sin20°的值为.11.已知函数,则f(x)的最大值为.12.若a=log43,则4a﹣4﹣a=.13.已知函数f(x)=ax+b(a>0,a≠1)的定义域和值域都是[﹣1,0],则a+b=.14.设S,T是R的两个非空子集,如果存在一个从S到T的函数y=f(x)满足:(1)T={f(x)|x∈S};(2)对任意x1,x2∈S,当x1<x2时,恒有f(x1)<f(x2).那么称这两个集合“保序同构”,现给出以下4对集合:①S={0,1,2},T={2,3};②S=N,T=N*;③S={x|﹣1<x<3},T={x|﹣8<x<10};④S={x|0<x<1},T=R.其中,“保序同构”的集合对的序号是(写出所有“保序同构”的集合对的序号).三、解答题:本大题共6个小题,共52分,解答应写出文字说明,证明过程或演算步骤.15.已知集合A={0,1},B={x|x2﹣ax=0},且A∪B=A,求实数a的值.16.设θ为第二象限角,若.求(Ⅰ)tanθ的值;(Ⅱ)的值.17.已知函数.(Ⅰ)证明:f(x)是奇函数;(Ⅱ)用函数单调性的定义证明:f(x)在(0,+∞)上是增函数.18.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:ωx+φ0π2πxAsin(ωx+φ)05﹣50(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.19.某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系y=ekx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0℃的保鲜时间为192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.20.若实数x,y,m满足|x﹣m|>|y﹣m|,则称x比y远离m.(Ⅰ)比较log20.6与20.6哪一个远离0;(Ⅱ)已知函数f(x)的定义域,任取x∈D,f(x)等于sinx和cosx中远离0的那个值,写出函数f(x)的解析式以及f(x)的三条基本性质(结论不要求证明).2015-2016学年北京市东城区高一(上)期末数学试卷参考答案与试题解析一、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,选出符合题目要求的一项并填在答题卡中.1.已知集合A={0,1,2},B={2,3},则集合A∪B=()A.{1,2,3}B.{0,1,2,3}C.{2}D.{0,1,3}【考点】并集及其运算.【专题】计算题;集合思想;综合法;集合.【分析】根据并集的运算性质计算即可.【解答】解: 集合A={0,1,2},B={2,3},则集合A∪B={0,1,2,3},故选:B.【点评】本题考查了集合的并集的运算,是一道基础题.2.若角α的终边经过点P(1,﹣2),则tanα的值为()A.B.C.﹣2D.【考点】任意角的三角函数的定义.【专题】计算题;方程思想;综合法;三角函数的图像与性质.【...