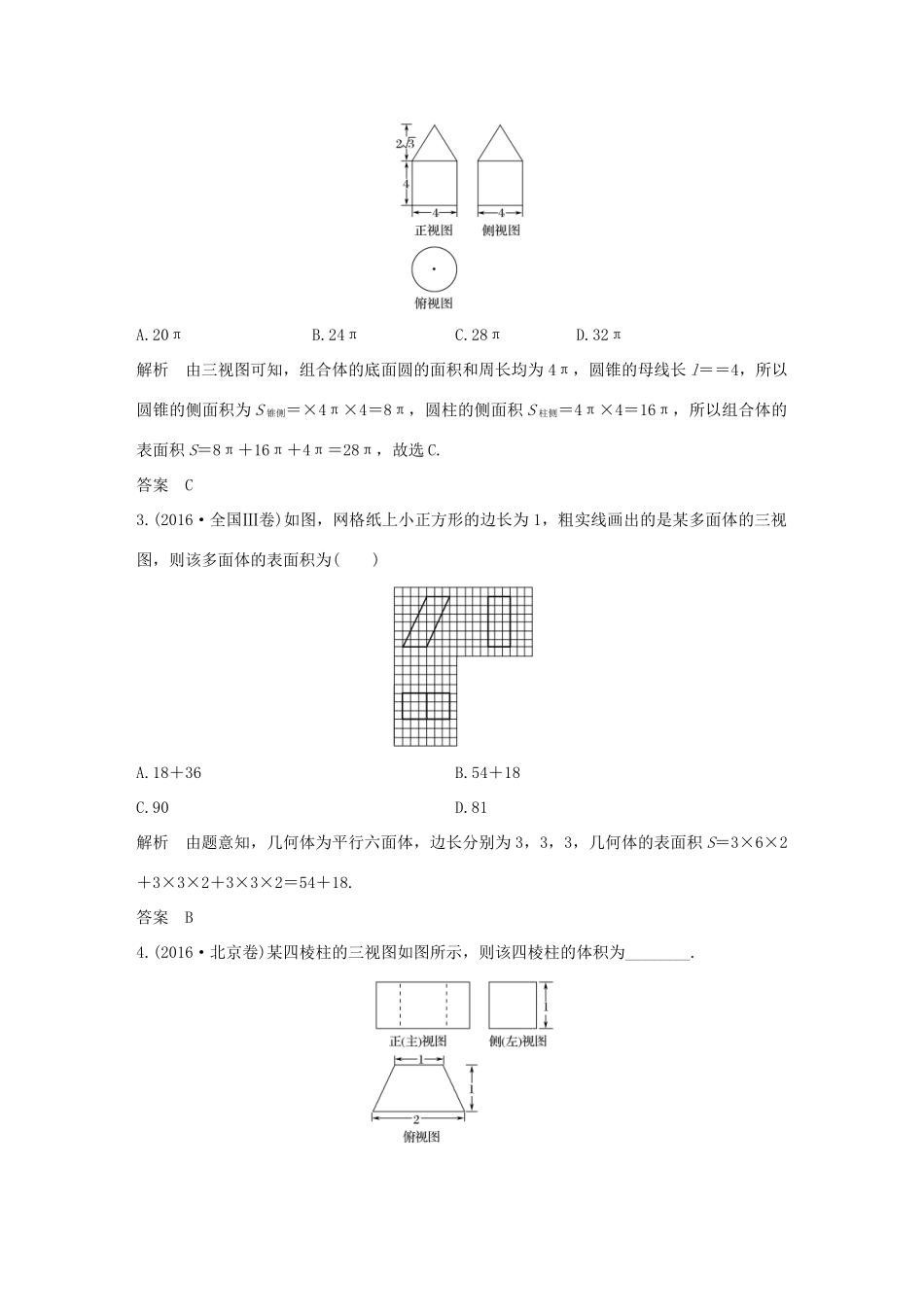
第1讲空间几何体中的计算高考定位1.以三视图为载体,考查空间几何体面积、体积的计算;2.考查空间几何体的侧面展开图及简单的组合体问题.真题感悟1.(2016·全国Ⅰ卷)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.20πD.28π解析由题知,该几何体的直观图如图所示,它是一个球(被过球心O且互相垂直的三个平面)切掉左上角的后得到的组合体,其表面积是球面面积的和三个圆面积之和,易得球的半径为2,则得S=×4π×22+3×π×22=17π,故选A.答案A2.(2016·全国Ⅱ卷)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()A.20πB.24πC.28πD.32π解析由三视图可知,组合体的底面圆的面积和周长均为4π,圆锥的母线长l==4,所以圆锥的侧面积为S锥侧=×4π×4=8π,圆柱的侧面积S柱侧=4π×4=16π,所以组合体的表面积S=8π+16π+4π=28π,故选C.答案C3.(2016·全国Ⅲ卷)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.18+36B.54+18C.90D.81解析由题意知,几何体为平行六面体,边长分别为3,3,3,几何体的表面积S=3×6×2+3×3×2+3×3×2=54+18.答案B4.(2016·北京卷)某四棱柱的三视图如图所示,则该四棱柱的体积为________.解析由三视图知该四棱柱为直四棱柱,底面积S==,高h=1,所以四棱柱体积V=S·h=×1=.答案考点整合1.四棱柱、直四棱柱、正四棱柱、正方体、平行六面体、直平行六面体、长方体之间的关系.2.几何体的摆放位置不同,其三视图也不同,需要注意长对正,高平齐,宽相等.3.空间几何体的两组常用公式(1)柱体、锥体、台体的侧面积公式:①S柱侧=ch(c为底面周长,h为高);②S锥侧=ch′(c为底面周长,h′为斜高);③S台侧=(c+c′)h′(c′,c分别为上下底面的周长,h′为斜高);④S球表=4πR2(R为球的半径).(2)柱体、锥体和球的体积公式:①V柱体=Sh(S为底面面积,h为高);②V锥体=Sh(S为底面面积,h为高);③V球=πR3.热点一以三视图为载体的几何体的表面积与体积的计算[微题型1]以三视图为载体求几何体的表面积【例1-1】(1)(2015·安徽卷)一个四面体的三视图如图所示,则该四面体的表面积是()A.1+B.1+2C.2+D.2(2)(2016·浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是________cm2,体积是________cm3.解析(1)由几何体的三视图可知空间几何体的直观图如图所示.∴其表面积S表=2××2×1+2××()2=2+,故选C.(2)由三视图可知该几何体由一个正方体和一个长方体组合而成,上面正方体的边长为2cm,下面长方体是底面边长为4cm,高为2cm,其直观图如右图:其表面积S=6×22+2×42+4×2×4-2×22=80(cm2).体积V=2×2×2+4×4×2=40(cm3).答案(1)C(2)8040探究提高(1)若以三视图的形式给出,解题的关键是对给出的三视图进行分析,从中发现几何体中各元素间的位置关系及数量关系,得到几何体的直观图,然后根据条件求解.(2)多面体的表面积是各个面的面积之和,组合体的表面积应注意重合部分的处理.[微题型2]以三视图为载体求几何体的体积【例1-2】(1)(2016·郑州模拟)已知一个几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.(4+π)(2)(2016·衡水大联考)如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是多面体的三视图,则该多面体的体积为()A.B.8C.D.解析(1)由该几何体的三视图,可知该几何体是由底面半径为1、高为、母线长为2的半圆锥,和底面为等腰三角形(底边长为2、高为2)、高为的三棱锥拼成的一个组合体.所以此组合体的体积为××π×12×+××2×2×=.(2)由图知此几何体为边长为2的正方体裁去一个三棱锥.所以此几何体的体积为2×2×2-××1×2×2=.故选C.答案(1)C(2)C探究提高解决此类问题需先由三视图确定几何体的结构特征,判断是否为组合体,由哪些简单几何体构成,并准确判断这些几何体之间的关系,将其切割为一些简单的几何体,再求出各个简单几何体的体积,最后求出组合体的体积.[微题型3]与球有关的体积问题【例1-3】(1)已知A,B...