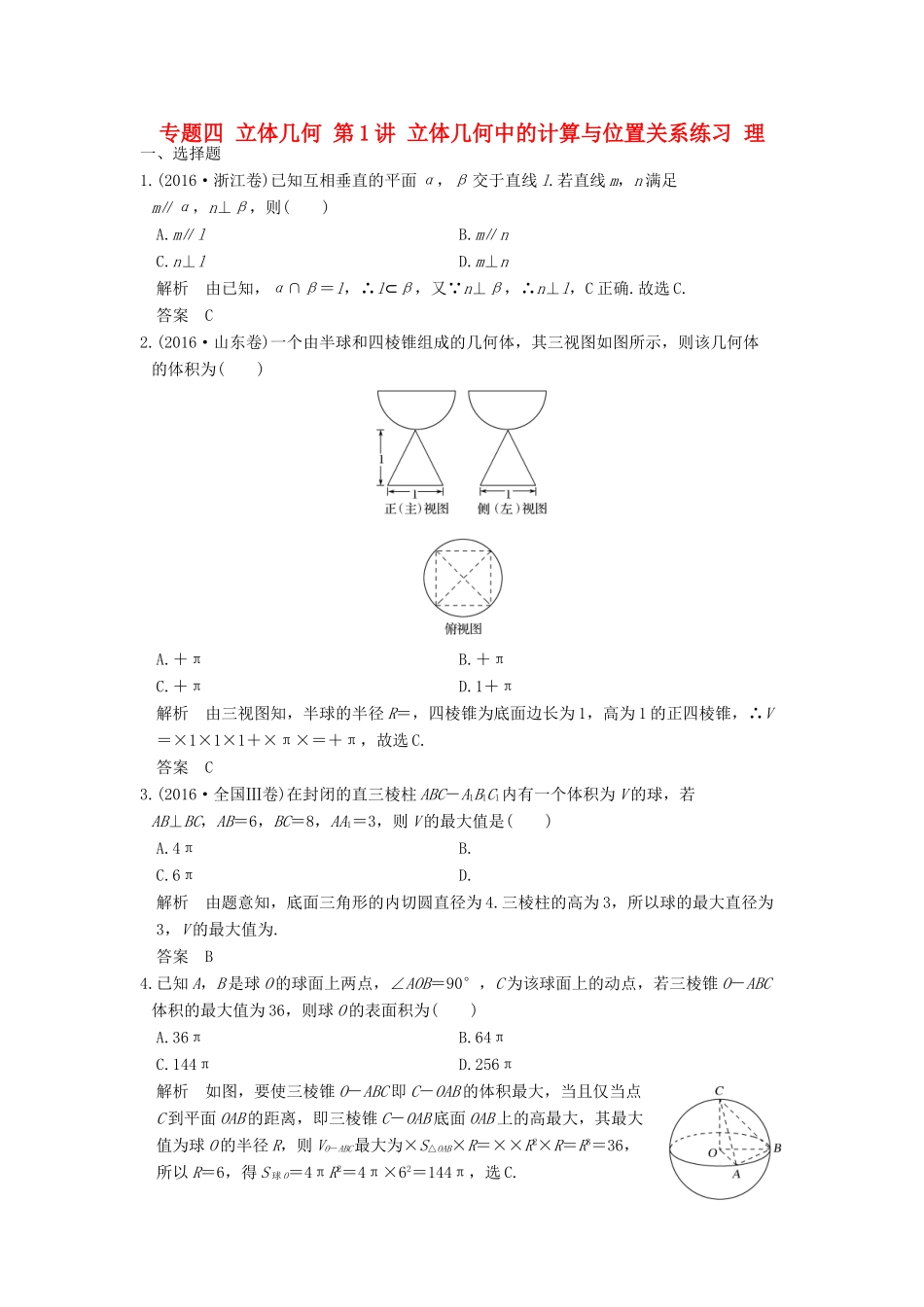
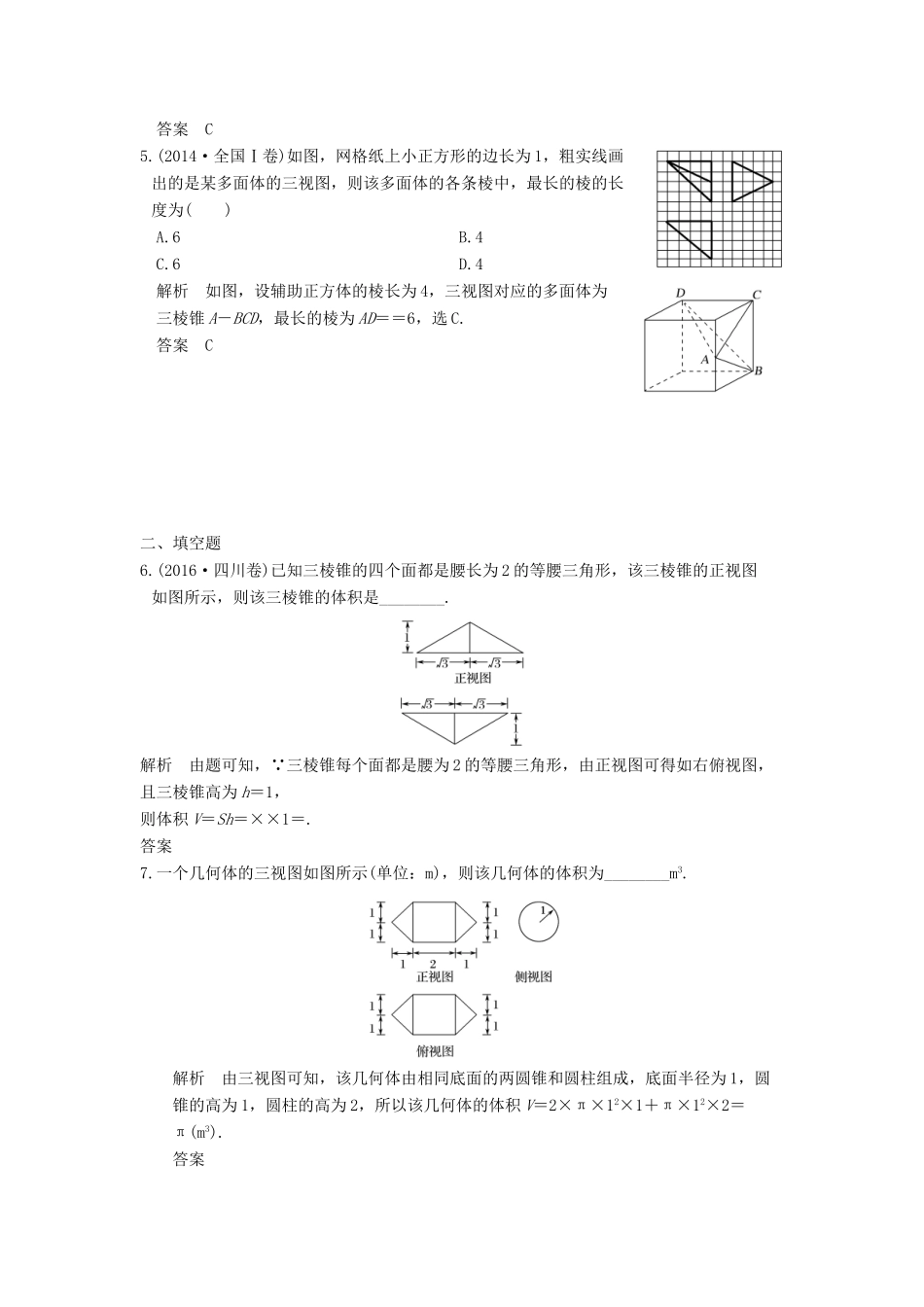
专题四立体几何第1讲立体几何中的计算与位置关系练习理一、选择题1.(2016·浙江卷)已知互相垂直的平面α,β交于直线l.若直线m,n满足m∥α,n⊥β,则()A.m∥lB.m∥nC.n⊥lD.m⊥n解析由已知,α∩β=l,∴l⊂β,又∵n⊥β,∴n⊥l,C正确.故选C.答案C2.(2016·山东卷)一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为()A.+πB.+πC.+πD.1+π解析由三视图知,半球的半径R=,四棱锥为底面边长为1,高为1的正四棱锥,∴V=×1×1×1+×π×=+π,故选C.答案C3.(2016·全国Ⅲ卷)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是()A.4πB.C.6πD.解析由题意知,底面三角形的内切圆直径为4.三棱柱的高为3,所以球的最大直径为3,V的最大值为.答案B4.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为()A.36πB.64πC.144πD.256π解析如图,要使三棱锥O-ABC即C-OAB的体积最大,当且仅当点C到平面OAB的距离,即三棱锥C-OAB底面OAB上的高最大,其最大值为球O的半径R,则VO-ABC最大为×S△OAB×R=××R2×R=R3=36,所以R=6,得S球O=4πR2=4π×62=144π,选C.答案C5.(2014·全国Ⅰ卷)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()A.6B.4C.6D.4解析如图,设辅助正方体的棱长为4,三视图对应的多面体为三棱锥A-BCD,最长的棱为AD==6,选C.答案C二、填空题6.(2016·四川卷)已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是________.解析由题可知,∵三棱锥每个面都是腰为2的等腰三角形,由正视图可得如右俯视图,且三棱锥高为h=1,则体积V=Sh=××1=.答案7.一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.解析由三视图可知,该几何体由相同底面的两圆锥和圆柱组成,底面半径为1,圆锥的高为1,圆柱的高为2,所以该几何体的体积V=2×π×12×1+π×12×2=π(m3).答案8.一个四面体的三视图如图所示,则该四面体的表面积是________.解析由空间几何体的三视图可得该空间几何体的直观图,如图,∴该四面体的表面积为S表=2××2×1+2××()2=2+.答案2+三、解答题9.在正三角形ABC中,E,F,P分别是AB,AC,BC边上的点,满足AE∶EB=CF∶FA=CP∶PB=1∶2(如图1),将△AEF折起到△A1EF的位置,连接A1B,A1C(如图2).(1)求证:FP∥平面A1EB;(2)求证:EF⊥A1B.证明(1)∵CP∶PB=CF∶FA,∴FP∥BE,又BE⊂平面A1EB,FP⊄平面A1EB,∴FP∥平面A1EB.(2)不妨设正三角形ABC的边长为3,则AE=1,AF=2.又∵∠EAF=60°,∴EF2=AE2+AF2-2AE·AFcos∠EAF=12+22-2×1×2cos60°=3,∴EF=.在△AEF中,有AF2=AE2+EF2,∴EF⊥AE,即EF⊥AB.则在题图2中,有EF⊥A1E,EF⊥BE,又A1E,BE⊂平面A1BE,A1E∩BE=E,∴EF⊥平面A1EB,又∵A1B⊂平面A1EB,∴EF⊥A1B.10.(2017·江南十校联考)如图1,等腰梯形ABCD中,BC∥AD,CE⊥AD,AD=3BC=3,CE=1.求△CDE沿CE折起得到四棱锥F-ABCE(如图2),G是AF的中点.(1)求证:BG∥平面ECE;(2)当平面FCE⊥平面ABCE时,求三棱锥F-BEG的体积.(1)证明如图,取EF的中点M,连接GM、MC,则GM綉AE.∵等腰梯形ABCD中,BC=1,AD=3,∴BC綉AE.∴GM綉BC,∴四边形BCMG是平行四边形,∴BG∥CM.又CM⊂平面FCE,BG⊄平面FCE,∴BG∥平面FCE.(2)解∵平面FCE⊥平面ABCE,平面FCE∩平面ABCE=CE,EF⊂平面FCE,FE⊥CE,∴FE⊥平面ABCE.又VF-BEG=VB-GEF=VB-AEF=VF-ABE,S△ABE=×2×1=1,∴VF-BEG=××1×1=.11.如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE.(1)求证:AE⊥BE;(2)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.(1)证明∵AD⊥平面ABE,AD∥BC,∴BC⊥平面ABE,∵AE⊂平面ABE,∴AE⊥BC.又∵BF⊥平面ACE,AE⊂平面ACE,∴AE⊥BF.∵BC∩BF=B,BC,BF⊂平面BCE,∴AE⊥平面BCE.又BE⊂平面BCE,∴AE⊥BE.(2)解在△ABE中过M点作MG∥AE交BE于G点,在△BEC中过G点作GN∥BC交EC于N点,连接MN,则由比例关系易得CN=CE.∵MG∥AE,MG⊄平面ADE,AE⊂平面ADE,∴MG∥平面ADE.同理,GN∥平面ADE.又∵GN∩MG=G,GN,MG⊂平面MGN,∴平面MGN∥平面ADE.又MN⊂平面MGN,∴MN∥平面ADE.∴N点为线段CE上靠近C点的一个三等分点.