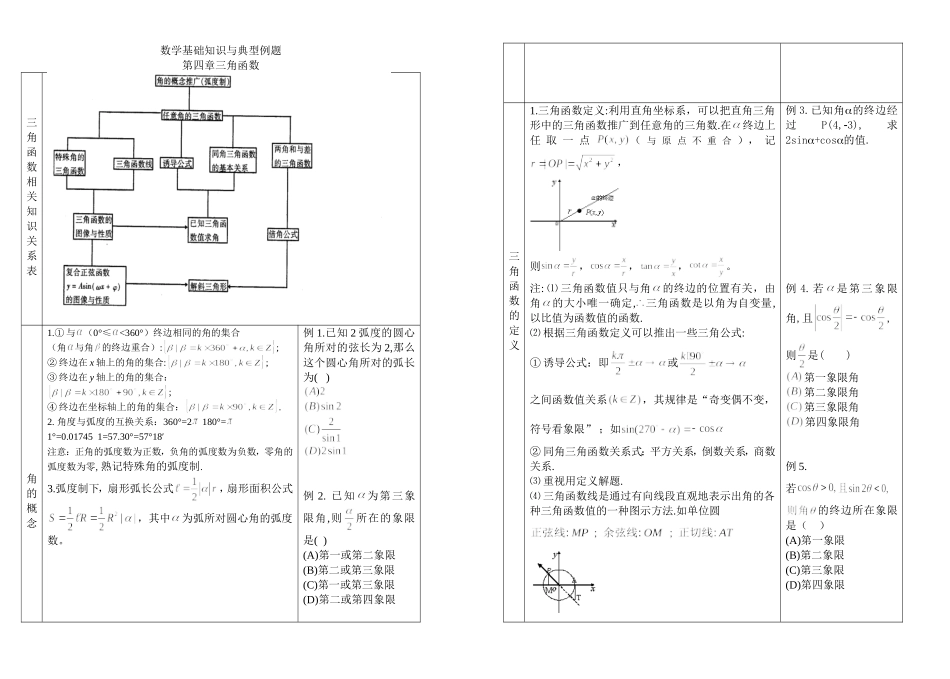
数学基础知识与典型例题第四章三角函数三角函数相关知识关系表角的概念1.①与(0°≤<360°)终边相同的角的集合(角与角的终边重合):;②终边在x轴上的角的集合:;③终边在y轴上的角的集合:;④终边在坐标轴上的角的集合:.2.角度与弧度的互换关系:360°=2180°=1°=0.017451=57.30°=57°18′注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零,熟记特殊角的弧度制.3.弧度制下,扇形弧长公式,扇形面积公式,其中为弧所对圆心角的弧度数。例1.已知2弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为()例2.已知为第三象限角,则所在的象限是()(A)第一或第二象限(B)第二或第三象限(C)第一或第三象限(D)第二或第四象限三角函数的定义1.三角函数定义:利用直角坐标系,可以把直角三角形中的三角函数推广到任意角的三角数.在终边上任取一点(与原点不重合),记,则,,,。注:⑴三角函数值只与角的终边的位置有关,由角的大小唯一确定,三角函数是以角为自变量,以比值为函数值的函数.⑵根据三角函数定义可以推出一些三角公式:①诱导公式:即或之间函数值关系,其规律是“奇变偶不变,符号看象限”;如②同角三角函数关系式:平方关系,倒数关系,商数关系.⑶重视用定义解题.⑷三角函数线是通过有向线段直观地表示出角的各种三角函数值的一种图示方法.如单位圆例3.已知角的终边经过P(4,3),求2sin+cos的值.例4.若是第三象限角,且,则是()第一象限角第二象限角第三象限角第四象限角例5.若的终边所在象限是()(A)第一象限(B)第二象限(C)第三象限(D)第四象限2.各象限角的各种三角函数值符号:一全二正弦,三切四余弦,(纵坐标y的符号)(横坐标x的符号)三角函数公式三角函数的公式:(一)基本关系公式组二()公式组三公式组四公式组五公式组六(二)两角和与差公式公式组一例6.化简:例7.已知tanα,tanβ是方程两根,且α,β,则α+β等于()(A)(B)或(C)或(D)例8.的公式组二:,1cossin1costan21cos1cossin公式组三1cos()sin2,1cos()sin2,1sin()cos21sin()cos2,1tan()cot2,1tan()cot2常用数据:的三角函数值,,值是()(A)2(B)2+3(C)4(D)334三角函数公式注:⑴以上公式务必要知道其推导思路,从而清晰地“看出”它们之间的联系,它们的变化形式.如等.从而可做到:正用、逆用、变形用自如使用各公式.⑵三角变换公式除用来化简三角函数式外,还为研究三角函数图象及性质做准备.⑶三角函数恒等变形的基本策略。①常值代换:特别是用“1”的代换,如1=cos2θ+sin2θ=tanx·cotx=tan45°等。②项的分拆与角的配凑。如分拆项:;配凑角(常用角变换):例9.设,若则=()(A)(B)(C)(D)4例10.()、、、、等.③降次与升次。即倍角公式降次与半角公式升次。④化弦(切)法。将三角函数利用同角三角函数基本关系化成弦(切)。⑤引入辅助角。asinθ+bcosθ=sin(θ+),这里辅助角所在象限由a、b的符号确定,角的值由tan=确定。例11.求下列各式的值:⑴;⑵tan17°+tan28°+tan17°tan28°例12.已知为锐角,且,求的值.三角函数公式例13.已知α为第二象限角,且sinα=求的值.例14.已知,(1)求的值;(2)求的值奎屯新疆王新敞例15.已知,三角例16.已知,求例17.已知锐角,b满足cos=,cos(+b)=,求cosb.函数公式例18.已知,,tan=,tanb=,求2+b.例19.在△ABC中,已知cosA=,sinB=,则cosC的值为()(A)(B)(C)(D)例20.若关于x的方程2cos2(+x)sinx+a=0有实根,求实数a的取值范围。三角函数三角函数的性质:(A、>0)定义域RRR值域周期性奇偶性奇函数偶函数当非奇非偶,当奇函数单调性上为增函数;上为减函数.()上为增函数;上为减函数.()上为增函数;上为减函数()三角函数定义域值域RR周期性奇偶性奇函数奇函数单调性上为增函数()上为减函数()以上性质的理解记忆关键是能想象或画出函数图象.函数的图像和性质以函数为基础,通过图像变换来把握.如①②(A>0,>0)相应地,①的单调增区间的解集是②的增区间.注:⑴或()的周期;⑵的对称轴方程是(),对称中心;的对称轴方程是(),对...