三角恒等变换复习课件VIP免费

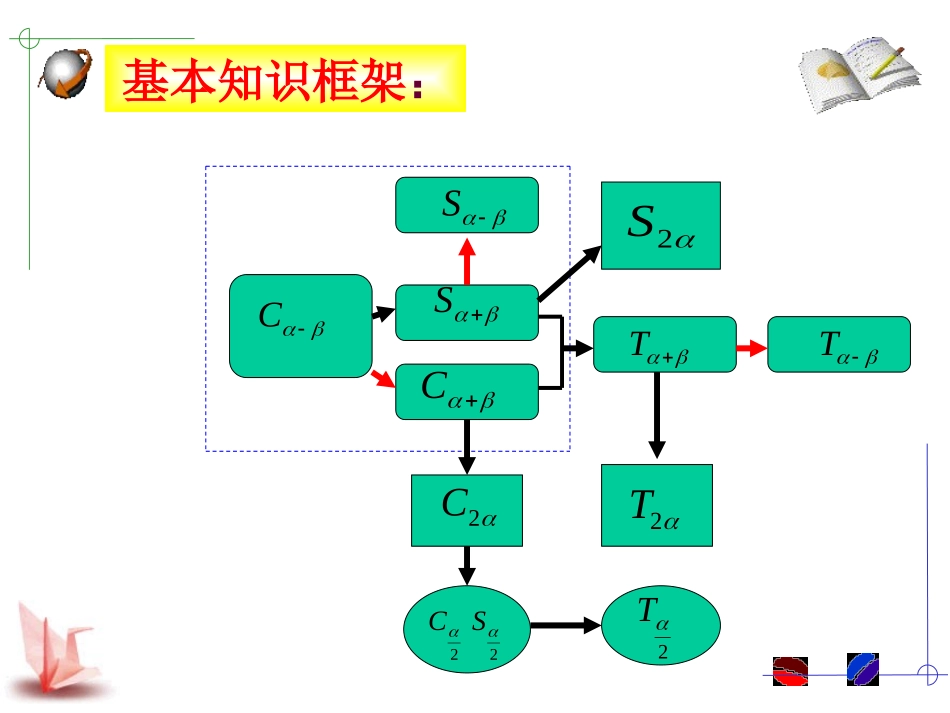
三角恒等变换复习CCSS2C2S2TTT2C2S2T基本知识框架：xbxacossin22ba22ba.cossin2222确定，由其中baabab2、辅助角公式说明：利用辅助角公式可以将形如的函数，转化为一个角的一种三角函数形式。便于后面求三角函数的最小正周期、最大（小）值、单调区间等。=sin+cosyab这个公式有什么作用？)cossin(2222xbabxbaa)cossinsin(cosxx.)sin(x22ba类型1：三角函数的化简例1计算：（公式变，逆用）(1)cos74sin14sin74cos14(2)3sincosxx(3)sin20cos110cos160sin70(4)sin15cos15tan12tan33(5)1tan12tan33322sin()62cos()3xx或1411113cos,cos()714例2：已知，为锐角，的值求cos类型2：三角函数求值01413)cos(,71cos又,1433)sin(,734sin9823sin)sin(cos)cos(])cos[(cos注：⑴常用角的变换：①②③④⑤⑵注意对角范围的要求。)()()(2)(222)4()4([借题发挥]解决此类问题的关键在于寻找条件和结论中的角的关系，分析角与角之间的互余、互补关系，合理拆、凑，把未知角用已知角表示．为锐角，解：变式练习：sin(2)sin2cos()sinsin例3：求证类型3：三角恒等证明sinsin)cos(2)2sin(sinsin)cos(2])sin[(sinsin)cos(cos)sin(sinsin右边证明：左边sinsin)cos(2sin)2sin([借题发挥]证明的本质是化异为同，可以说，证明是有目标的有目的化简.左右归一或变更结论，常用定义法、化弦法、拆项拆角法、1的变换法、公式变形法等方法．类型4:三角恒等变换与三角函数的联系22.()cos2sin,().fxxxfx例已知函数求的单调增区间1cos211()cos2cos2.222xfxxx解：+2k2x2k,kZf(x)kxk,kZ.2当时，为增函数，即f(x)k,k(kZ).2函数的单调增区间为三角恒等变换实际上是对角、函数名称，以及函数形（结构）的变换，这类问题，无论是求值化简证明以及复杂的综合问题，一般的考虑方法是：⑴找差异：角、名、形的差异；⑵建立关系：角的和差关系、倍半关系等，名、形之间可以用哪个公式联系起来；⑶变公式：在实际变换过程中，往往需要将公式加以变形后，正用或逆用公式.课堂小结：