图论及应用第一章完整作业VIP免费

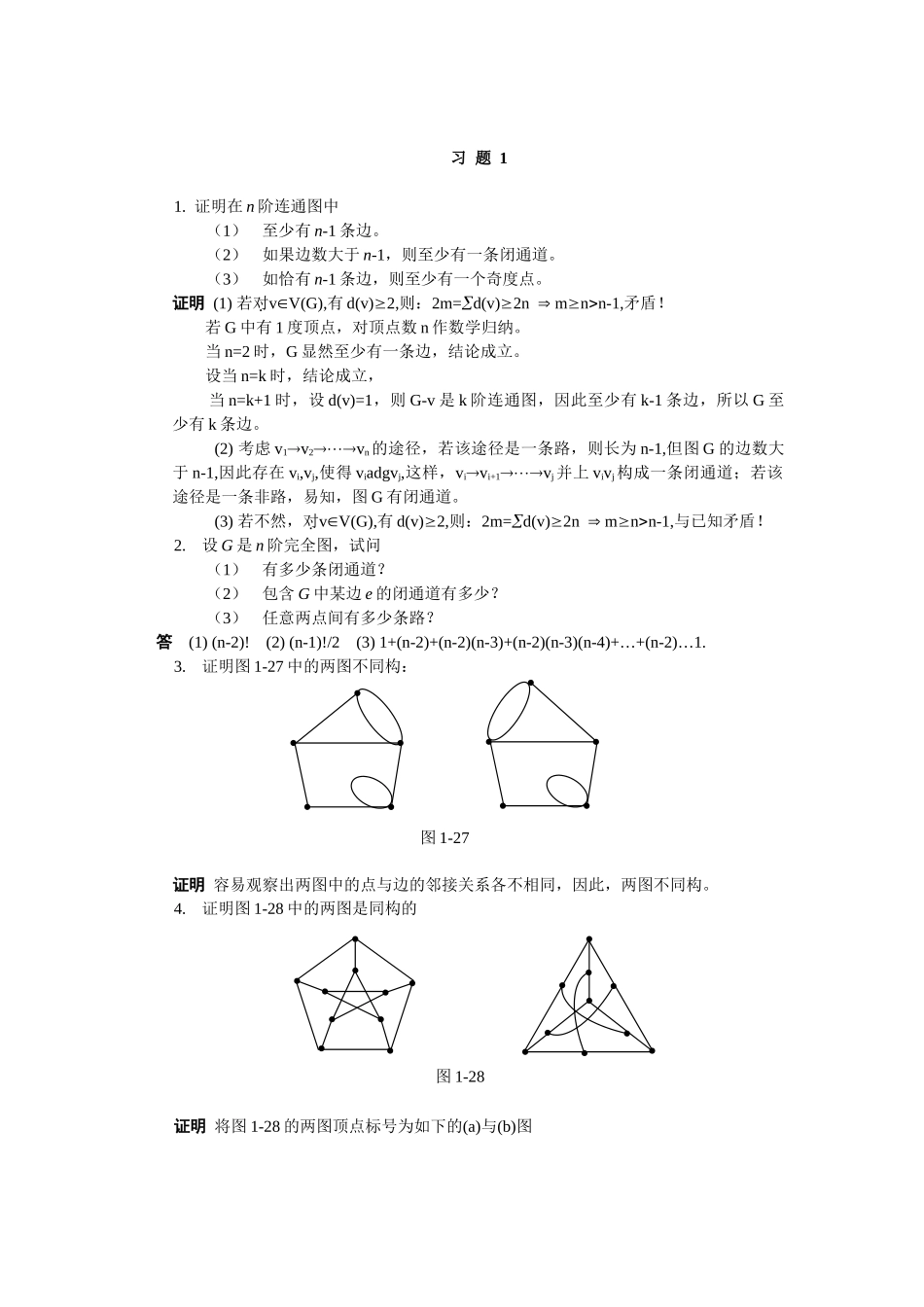
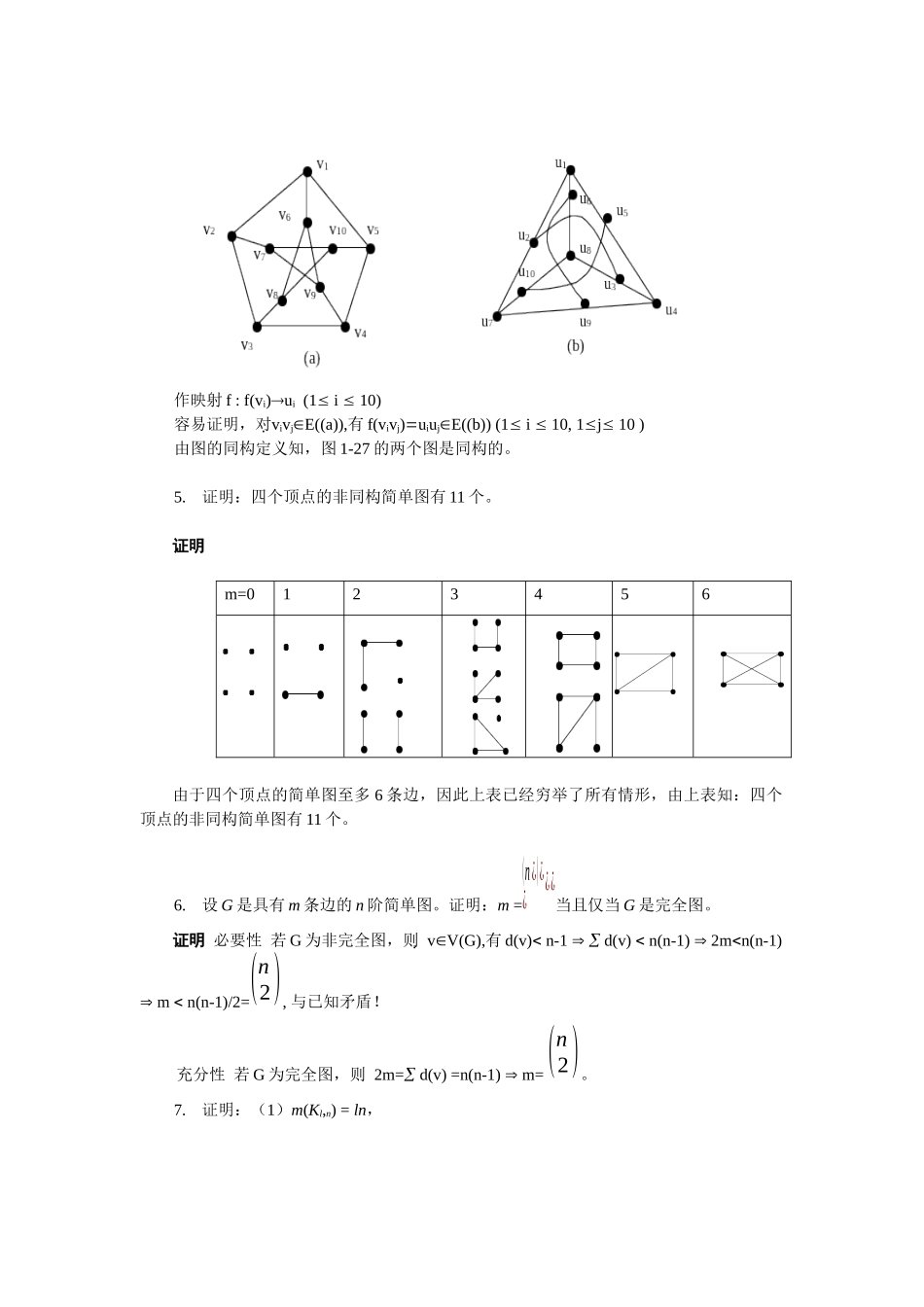
习题11.证明在n阶连通图中（1）至少有n-1条边。（2）如果边数大于n-1，则至少有一条闭通道。（3）如恰有n-1条边，则至少有一个奇度点。证明(1)若对vV(G),有d(v)2,则：2m=d(v)2nmnn-1,矛盾！若G中有1度顶点，对顶点数n作数学归纳。当n=2时，G显然至少有一条边，结论成立。设当n=k时，结论成立，当n=k+1时，设d(v)=1，则G-v是k阶连通图，因此至少有k-1条边，所以G至少有k条边。(2)考虑v1v2vn的途径，若该途径是一条路，则长为n-1,但图G的边数大于n-1,因此存在vi,vj,使得viadgvj,这样，vivi+1vj并上vivj构成一条闭通道；若该途径是一条非路，易知，图G有闭通道。(3)若不然，对vV(G),有d(v)2,则：2m=d(v)2nmnn-1,与已知矛盾！2.设G是n阶完全图，试问（1）有多少条闭通道？（2）包含G中某边e的闭通道有多少？（3）任意两点间有多少条路？答(1)(n-2)!(2)(n-1)!/2(3)1+(n-2)+(n-2)(n-3)+(n-2)(n-3)(n-4)+…+(n-2)…1.3.证明图1-27中的两图不同构：证明容易观察出两图中的点与边的邻接关系各不相同，因此，两图不同构。4.证明图1-28中的两图是同构的证明将图1-28的两图顶点标号为如下的(a)与(b)图图1-27图1-28作映射f:f(vi)ui(1i10)容易证明，对vivjE((a)),有f(vivj)uiujE((b))(1i10,1j10)由图的同构定义知，图1-27的两个图是同构的。5.证明：四个顶点的非同构简单图有11个。证明m=0123456由于四个顶点的简单图至多6条边，因此上表已经穷举了所有情形，由上表知：四个顶点的非同构简单图有11个。6.设G是具有m条边的n阶简单图。证明：m=(n¿)¿¿¿¿当且仅当G是完全图。证明必要性若G为非完全图，则vV(G),有d(v)n-1d(v)n(n-1)2mn(n-1)mn(n-1)/2=(n2),与已知矛盾！充分性若G为完全图，则2m=d(v)=n(n-1)m=(n2)。7.证明：（1）m(Kl,n)=ln，（2）若G是具有m条边的n阶简单偶图，则m⌊n24⌋。证明(1)Kl,n的总度数为2ln,所以，m(Kl,n)=ln。(2)设G的两个顶点子集所含顶点数分别为n1与n2,G的边数为m,可建立如下的二次规划：m=n1n2s.tn1+n2=nn11,n21当n为偶数时，n1=n2=n/2时，m取最大值：m=n2/4当n为奇数时，取n1=(n+1)/2,n2=(n-1)/2时，m取最大值：m=(n2-1)/4所以，m⌊n24⌋。8.设△和δ是简单图G的最大度和最小度，则δ≤2m/n≤△。证明2m=∑v∈Vd(v)≥nδ⇒δ≤2mn2m=∑v∈Vd(v)=Δn⇒Δ≥2mn∴δ≤2mn≤Δ9.证明：若k正则偶图具有二分类V=V1∪V2，则|V1|=|V2|。证明由于G为k正则偶图，所以，kV1=m=kV2V1=V2。10.证明：由两人或更多个人组成的人群中，总有两人在该人群中恰好有相同的朋友数。证明将人用图的顶点表示，图的两顶点邻接当且仅当人群中的两人相认识，于是，问题转化为：证明在任意一个简单图中必有一对度数相等的顶点。若图G为连通单图，则对vV(G),有1d(v)n-1,因此，n个顶点中必存在两个顶点，其度数相同；若G为非连通图，设G1为阶数n1的连通分支，则vV(G1),有1d(v)n1-1，于是在G1中必存在两个顶点，其度数相同。11.证明：序列(7,6,5,4,3,3,2)和(6,6,5,4,3,3,1)不是图序列。证明由于7个顶点的简单图的最大度不会超过6，因此序列(7,6,5,4,3,3,2)不是图序列；(6,6,5,4,3,3,1)是图序列（5，4，3，2，2，0）是图序列，然（5，4，3，2，2，0）不是图序列，所以(6,6,5,4,3,3,1)不是图序列。12.证明：若δ≥2，则G包含圈。证明只就连通图证明即可。设V(G)=｛v1,v2,…,vn｝,对于G中的路v1v2…vk,若vk与v1邻接，则构成一个圈。若vi1vi2…vin是一条路，由于2，因此，对vin，存在点vik与之邻接，则vikvinvik构成一个圈。13.证明：若G是简单图且δ≥2，则G包含长至少是δ+1的圈。证明设v0v1…vk为G中一条最长路，则v0的邻接顶点一定在该路上，否则，与假设矛盾。现取与v0相邻的脚标最大者，记为l，则l,于是得圈v0v1v2vlv0,该圈长为l+1，显然不小于δ+1。`14.G的围长是指G中最短圈的长；若G没有圈，则定义G的围长为无穷大。证明：（1）围长为4的k的正则图至少有2k个顶点，且恰有2k个顶点的这样的图（在同构意义下）只有一个。（2）围长...