第六讲 随机过程的遍历性VIP免费

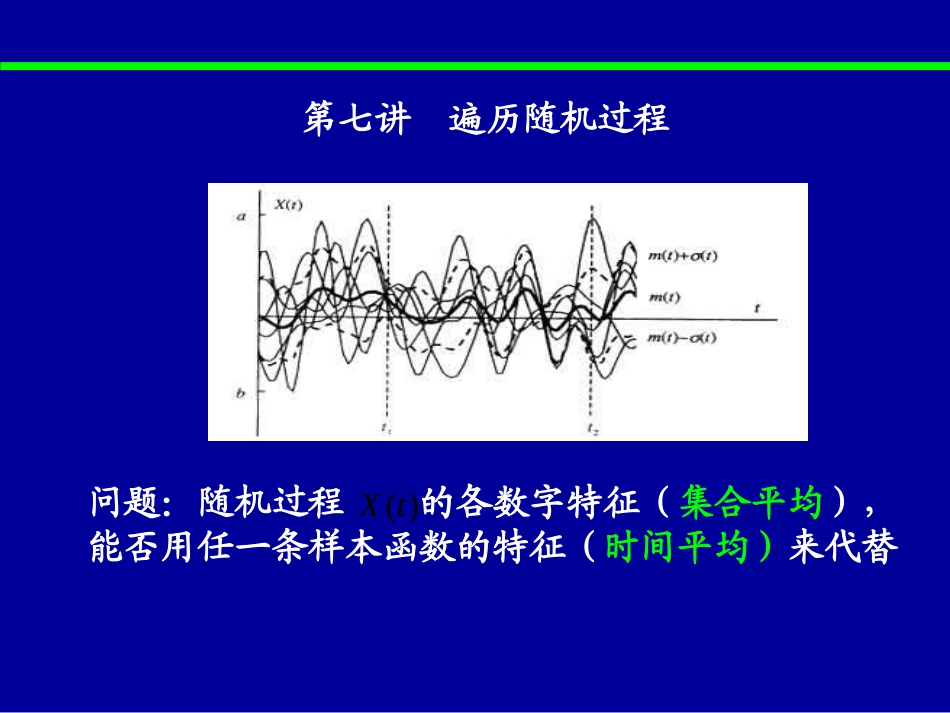
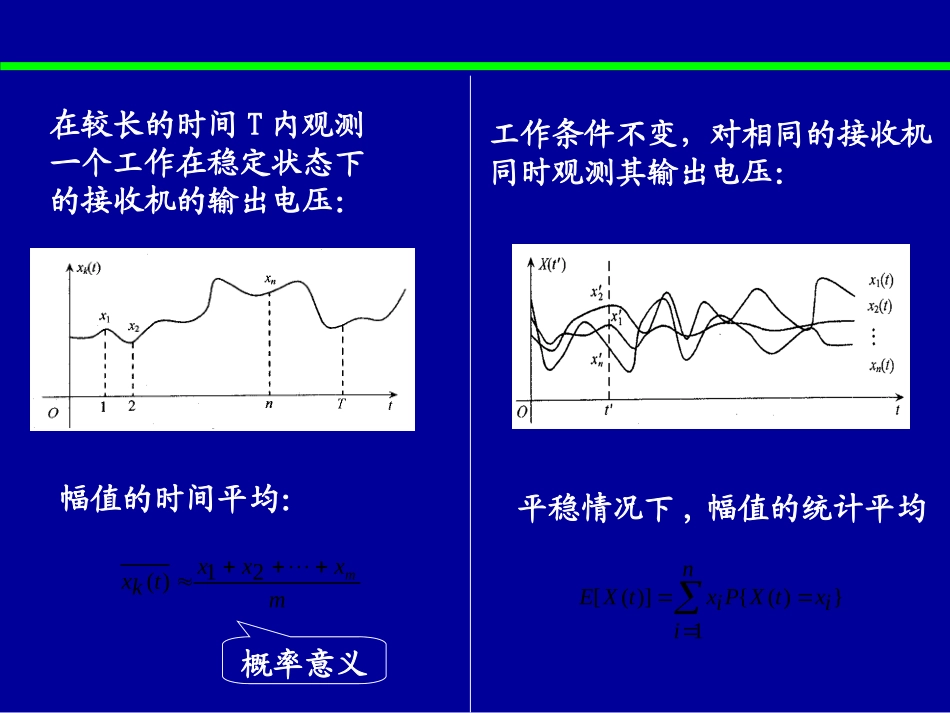
第七讲遍历随机过程问题：随机过程的各数字特征（集合平均），能否用任一条样本函数的特征（时间平均）来代替)(tX在较长的时间T内观测一个工作在稳定状态下的接收机的输出电压：mxxxtkxm21)(niixtXPixtXE1})({)]([工作条件不变，对相同的接收机同时观测其输出电压：幅值的时间平均：概率意义平稳情况下,幅值的统计平均1、均值各态历经性)]([)(tXEPtXTTdttXTTmiltX)(21)(代表随机信号的时间平均是时间t的函数，与取那条样本无关与取那条样本有关，与时间无关TTdttxTTmiltx)(21)(广义各态历经性的定义在相关理论的范围内讨论历经过程，即讨论两种时间平均：均值和自相关2、均值各态历经的条件和含义（重点）条件1、X（t）均值平稳TTdttxTTmiltXE)(21)]([任何一条样本函数所包含的取值状态与随机过程（任意时刻）所有的状态相同，而且出现的频率与随机过程各状态的概率相同)]([)(tXEPtXxm条件2、X（t）的时间平均与样本函数无关，即对各条样本函数的取值一样，)(tX0})({tXD)(tx均值各态历经3、自相关各态历经性TTTdttXtXTmiltXtXtXtX)()(21)()()()(21其中)]2()1([)2()1(tXtXEPtXtXTTTdttxtxTmiltxtx)()(21)()(NnNxmnxnxNmilmR1)()(1)(4、相关各态历经的条件和含义（重点）任何一条样本函数都同样的经历了随机过程的各种二阶可能状态)2,1()()(ttXRtXtX)(XR条件1、不是的函数，而是的函数，即随机过程相关平稳)2,1(ttXR2,1tt条件2、与样本函数无关，)()(tXtX)()(txtx0})()({tXtXD)()(txtxTTdttxtxTTmilRX)()(21)(相关各态历经在各条样本函数中可能状态相同，且以相同的概率出现5、各态历经性的定义设X(t)是一个平稳随机过程，如果同时满足均值各态历经、相关各态历经，则称x（t）广义各态历经)]([tXEPxm)(tx)2,1(ttXRP)(XR)()(txtx如果一个平稳随机过程X(t)，它的各种时间平均（时间足够长）与相应的统计平均以概率1相等则称X(t)具有严格的各态历经性，或该过程为严各态历经过程在实际应用中，如果随机过程是平稳的，我们总是凭经验假设它是各态历经的。6、假设随机过程各态历经的意义任何一个样本函数的特性都可以充分代表随机过程的全部统计特性，简化研究过程和实际统计方法实际中，在通信系统中，我们认为噪声和信号一般都是平稳和各态历经的各态历经的意义从定义(重点)dRX0)(零均值平稳正态随机信号：遍历性判断从充分条件均值遍历性：2)(XmXRTmil相关遍历性若不含周期分量例判断随机过程X(t)=Y的遍历性，其中Y是方差不为零的随机变量。解：yydtTtxTTT21lim)(][)]([YEtXE][)]()([2YEtXtXE平稳随机过程结论：一个随机变量一定不是各态历经的例判断是否具有遍历性，其中均匀分布于(0，2)。)cos()(0tAtX解、均值遍历性02021)cos()]cos([)]([dtataEtXE)}sin()sin({21lim)sin(21lim)(TaTaTTTTtaTTtx0limTaTTTTdtttaTTtxtx)cos()cos(21lim)()(2)(2/)cos(02XRa自相关遍历性)(tXt)(tXt(a)(b)各态历经性判别7、用实验手段研究随机过程的统计特性统计实验分析的理论基础：统计实验分析的目的：各态历经假设从时间序列（实验数据）出发（一个实现），估计它所代表的随机过程X（t）的统计特性均值、方差、相关函数、功率谱密度（频域特性），密度函数待估计的量：随机过程的数字特征估计均值函数：mean()用法：m=mean(x)功能：返回X(n)均值估计10)(1ˆNnnxNXm均值：估计方法的好坏评判无偏性有偏性渐进无偏估计量的期望：估计量的方差:一致估计方差越小越好无偏、一致估计量方差函数：var()用法：sigma2=var(x)功能：返回X(n)方差估计方差：标准方差函数：std()用法：sigma=std(x)功能：返回X(n)标准方差估计有偏（渐进无偏）、一致估计量102]ˆ)([12ˆNnmnxNXX自相关函数...