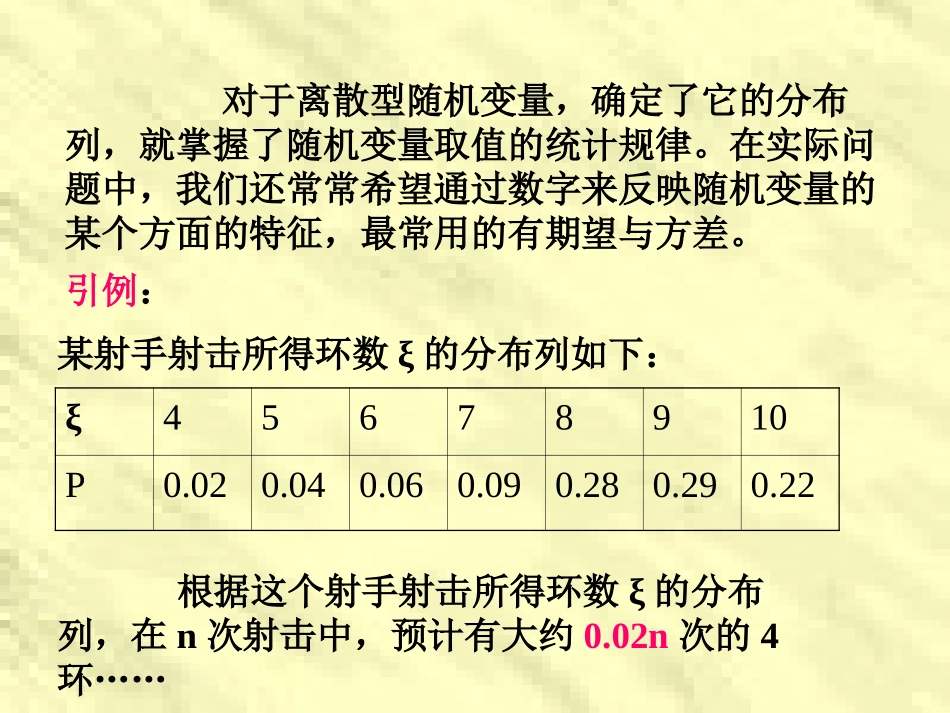
离散型随机变量的期望教学要求:使学生了解离散型随机变量的期望的意义,会根据离散型随机变量的分布列求出期望.对于离散型随机变量,确定了它的分布列,就掌握了随机变量取值的统计规律。在实际问题中,我们还常常希望通过数字来反映随机变量的某个方面的特征,最常用的有期望与方差。某射手射击所得环数ξ的分布列如下:ξ45678910P0.020.040.060.090.280.290.22引例:根据这个射手射击所得环数ξ的分布列,在n次射击中,预计有大约0.02n次的4环……1、期望类似地,对任一射手,若已知其射击所得环数ξ的分布列,即已知各个P(ξ=i)(i=0,1,2,3,…10),则可预计他任意n次射击的平均环数是Eξ=0×P(ξ=0)+1×P(ξ=1)+…+10×P(ξ=10)称Eξ为此射手射击所得环数ξ的期望,它刻划了随机变量ξ所取的平均值,从一个方面反映了射手的射击水平。若离散型随机变量ξ的概率分布为ξx1x2…xi…Pp1p2…pi…则称Eξ=x1p1+x2p2+…+xnpn+…为ξ的数学期望或平均数、均值,又称期望。问:若ξ为上述离散型随机变量,则η=aξ+b的分布列怎样?Eη呢?因为P(η=axi+b)=P(ξ=xi),i=1,2,3…所以,η的分布图为ηax1+bax2+b…axn+b…Pp1p2…pn…于是Eη=(ax1+b)p1+(ax2+b)p2+…+(axn+b)pn+…=a(x1p1+x2p2+…+xnpn+…)+b(p1+p2+…+pn+…)=aEξ+bE(aξ+b)=aEξ+b2、例题例1:随机抛掷一个骰子,求所得骰子的点数ξ的期望。例2有一批数量很大的产品,其次品率是15%。对这批产品进行抽查,每次抽出1件,如果抽出次品,则抽查终止,否则继续抽查,直到抽出次品,但抽查次数最多不超过10次。求抽查次数ξ的期望。(结果保留三个有效数字)解:抽查次数ξ取1~10的整数,从这批数量很大的产品中每次抽取一件检验的试验可以认为是彼此独立的,取出次品的概率是0.15,取出正品的概率是0.85,前k-1次取出正品而第k次(k=1,2,…9)取出次品的概率P(ξ=k)=g(k,0.15)=0.85k-1×0.15,(k=1,2,…9);需要抽查10次即前9次取出的都是正品的概率P(ξ=10)=0.859(为什么?)3、结论(1):若ξ~B(n,p),则Eξ=np∴Eξ=0×Cn0p0qn+1×Cn1p1qn-1+2×Cn2p2qn-2+…+k×Cnkpkqn-k+…+n×Cnnpnq0∵P(ξ=k)=Cnkpkqn-k证明:=np(Cn-10p0qn-1+Cn-11p1qn-2+…+Cn-1k-1pk-1q(n-1)-(k-1)+…+Cn-1n-1pn-1q0)=np(p+q)n-1=npξ01…k…nPCn0p0qnCn1p1qn-1…Cnkpkqn-k…Cnnpnq0(kC∵nk=nCn-1k-1)例4一次英语单元测验由20个选择题构成,每个选择题有4个选项。其中有且仅有一个是正确答案,每题选择正确答案得5分。不作出选择或选错不得分,满分100分。学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一个。求学生甲和学生乙在这次英语单元测验中的成绩的期望。服从二项分布的随机变量的期望若ξ~B(n,p),则Eξ=np例5:一次英语单元测验由20个选择题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分。学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一个。求学生甲和学生乙在这次英语单元测验中的成绩的期望。解:设学生甲和学生乙在这次英语测验中选择了正确答案的选择题个数分别是ξ和η,则ξ~B(20,0.9),η~B(20,0.25),Eξ=20×0.9=18,Eη=20×0.25=5.由于答对每题得5分,学生甲和学生乙在这次英语测验中的成绩分别是5ξ和5η。所以,他们在测验中的成绩的期望分别是E(5ξ)=5Eξ=5×18=90,E(5η)=5Eη=5×5=25.结论(2):若p(ξ=k)=g(k,p),则Eξ=1/p服从几何分布的随机变量的期望ξ123…k…Pppqpq2…pqk-1…∴Eξ=p+2pq+3pq2+…+kpqk-1+…qEξ=pq+2pq2+3pq3+…+kpqk+…∴(1-q)Eξ=p+pq+pq2+pq3+…+pqk+…11qpPqE111例5在独立重复的射击试验中,某人击中目标的概率为0.2,则他在射击时击中目标所需要的射击次数ξ的期望是多少?小结:1、随机变量的数学期望。2、公式3、若ξ~B(n,p),则Eξ=npE(aξ+b)=aEξ+b练习:P141~6。作业:习题1.2P161~64:公式若p(ξ=k)=g(k,p),则Eξ=1/p讲评作业:P9习题3,63、某射手射击击中目标的概率为0.9,求从开始射击到击中目标所需的射击次数ξ的概率分布。解:射击次数ξ的概率分布为ξ123…n…P0.90.090.009…0.1n-1×0.9…6、某批数量较大的商品的次品率为10%,从中任意地连续取出5件,求其中次品数ξ的分布列。解:ξ~B(5,0.1).ξ的分布列为ξ012345P0.590490.328050.07290.00810.000450.00001