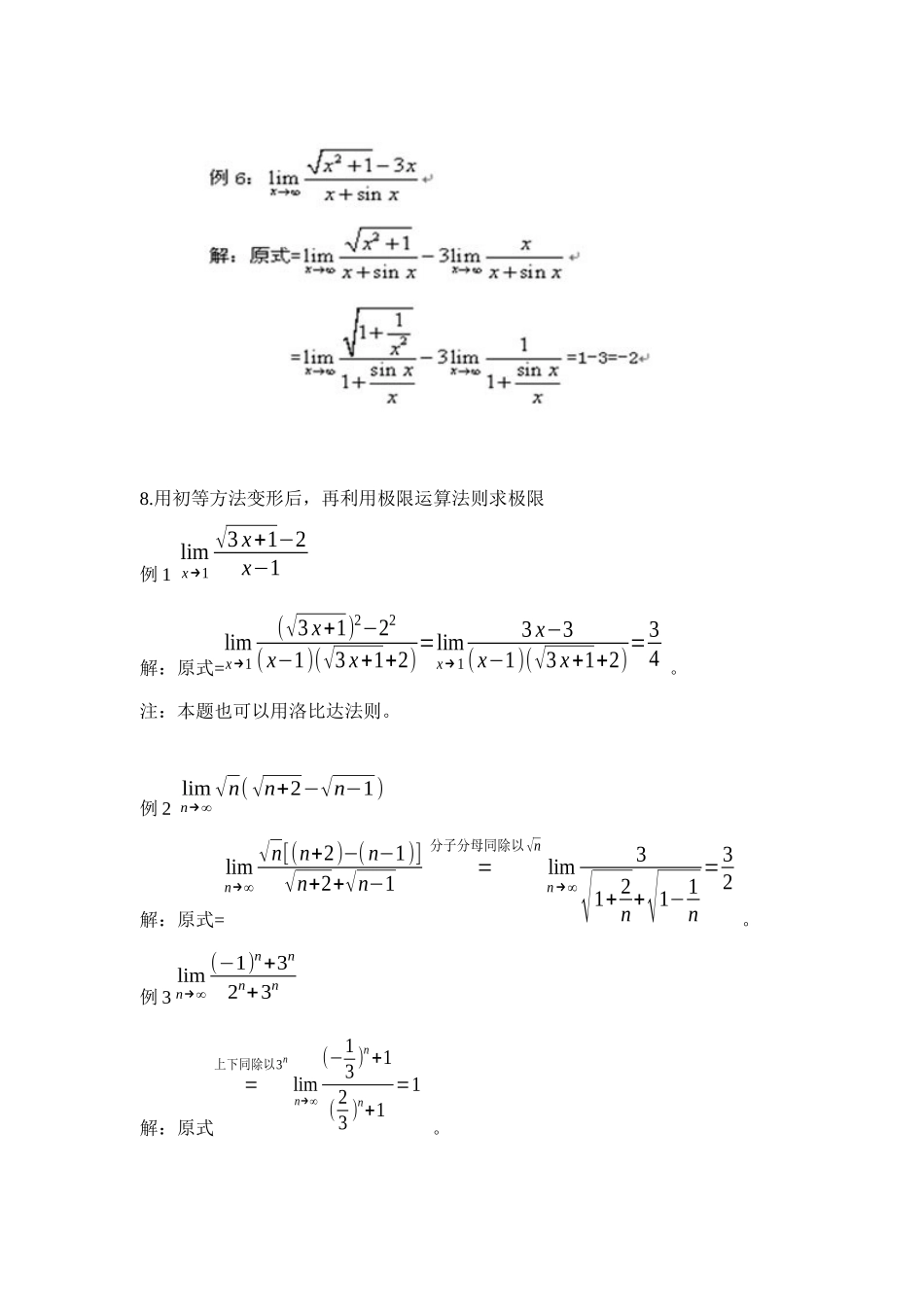
1.定义:说明:(1)一些最简单的数列或函数的极限(极限值可以观察得到)都可以用上面的极限严格定义证明,例如:;limx→2(3x−1)=5(2)在后面求极限时,(1)中提到的简单极限作为已知结果直接运用,而不需再用极限严格定义证明。利用导数的定义求极限这种方法要求熟练的掌握导数的定义。2.极限运算法则定理1已知limf(x),limg(x)都存在,极限值分别为A,B,则下面极限都存在,且有(1)lim[f(x)±g(x)]=A±B(2)limf(x)⋅g(x)=A⋅B(3)limf(x)g(x)=AB,(此时需B≠0成立)说明:极限号下面的极限过程是一致的;同时注意法则成立的条件,当条件不满足时,不能用。.利用极限的四则运算法求极限这种方法主要应用于求一些简单函数的和、乘、积、商的极限。通常情况下,要使用这些法则,往往需要根据具体情况先对函数做某些恒等变形或化简。8.用初等方法变形后,再利用极限运算法则求极限例1limx→1√3x+1−2x−1解:原式=limx→1(√3x+1)2−22(x−1)(√3x+1+2)=limx→13x−3(x−1)(√3x+1+2)=34。注:本题也可以用洛比达法则。例2limn→∞√n(√n+2−√n−1)解:原式=limn→∞√n[(n+2)−(n−1)]√n+2+√n−1=分子分母同除以√nlimn→∞3√1+2n+√1−1n=32。例3limn→∞(−1)n+3n2n+3n解:原式=上下同除以3nlimn→∞(−13)n+1(23)n+1=1。3.两个重要极限(1)limx→0sinxx=1(2)limx→0(1+x)1x=e;limx→∞(1+1x)x=e说明:不仅要能够运用这两个重要极限本身,还应能够熟练运用它们的变形形式,例如:limx→0sin3x3x=1,limx→0(1−2x)1−2x=e,limx→∞(1+3x)x3=e;等等。利用两个重要极限求极限例5limx→01−cosx3x2解:原式=limx→02sin2x23x2=limx→02sin2x212⋅(x2)2=16。注:本题也可以用洛比达法则。例6limx→0(1−3sinx)2x解:原式=limx→0(1−3sinx)1−3sinx⋅−6sinxx=limx→0[(1−3sinx)1−3sinx]−6sinxx=e−6。例7limn→∞(n−2n+1)n解:原式=。limn→∞(1+−3n+1)n+1−3⋅−3nn+1=limn→∞[(1+−3n+1)n+1−3]−3nn+1=e−34.等价无穷小定理2无穷小与有界函数的乘积仍然是无穷小(即极限是0)。定理3当x→0时,下列函数都是无穷小(即极限是0),且相互等价,即有:x~sinx~tanx~arcsinx~arctanx~ln(1+x)~ex−1。说明:当上面每个函数中的自变量x换成g(x)时(g(x)→0),仍有上面的等价关系成立,例如:当x→0时,e3x−1~3x;ln(1−x2)~−x2。定理4如果函数f(x),g(x),f1(x),g1(x)都是x→x0时的无穷小,且f(x)~f1(x),g(x)~g1(x),则当limx→x0f1(x)g1(x)存在时,limx→x0f(x)g(x)也存在且等于f(x)limx→x0f1(x)g1(x),即limx→x0f(x)g(x)=limx→x0f1(x)g1(x)。利用等价无穷小代换(定理4)求极限例9limx→0xln(1+3x)arctan(x2)解: x→0时,ln(1+3x)~3x,arctan(x2)~x2,原式=limx→0x⋅3xx2=3。例10limx→0ex−esinxx−sinx解:原式=limx→0esinx(ex−sinx−1)x−sinx=limx→0esinx(x−sinx)x−sinx=1。注:下面的解法是错误的:原式=limx→0(ex−1)−(esinx−1)x−sinx=limx→0x−sinxx−sinx=1。正如下面例题解法错误一样:limx→0tanx−sinxx3=limx→0x−xx3=0。例11limx→0tan(x2sin1x)sinx解: 当x→0时,x2sin1x是无穷小,∴tan(x2sin1x)x与2sin1x等价,所以,原式=limx→0x2sin1xx=limx→0xsin1x=0。(最后一步用到定理2)五、利用无穷小的性质求极限有限个无穷小的和是无穷小,有界函数与无穷小乘积是无穷小。用等价无穷小替换求极限常常行之有效。例1.2.5.洛比达法则定理5假设当自变量x趋近于某一定值(或无穷大)时,函数f(x)和g(x)满足:(1)f(x)和g(x)的极限都是0或都是无穷大;(2)f(x)和g(x)都可导,且g(x)的导数不为0;(3)limf'(x)g'(x)存在(或是无穷大);则极限limf(x)g(x)也一定存在,且等于limf'(x)g'(x),即limf(x)g(x)=limf'(x)g'(x)。说明:定理5称为洛比达法则,用该法则求极限时,应注意条件是否满足,只要有一条不满足,洛比达法则就不能应用。特别要注意条件(1)是否满足,即验证所求极限是否为“00”型或“∞∞”型;条件(2)一般都满足,而条件(3)则在求导完毕后可以知道是否满足。另外,洛比达法则可以连续使...