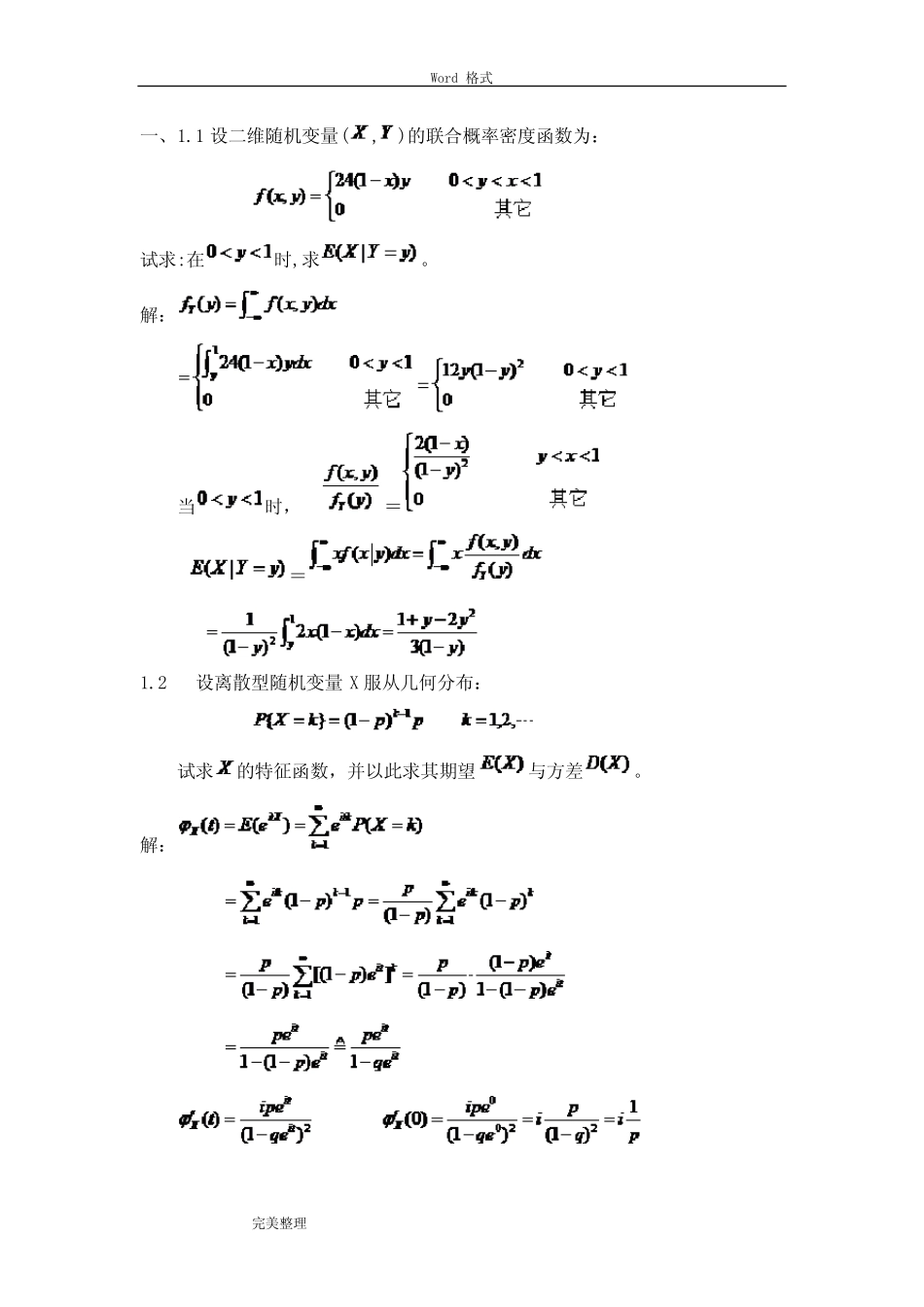Word格式完美整理一、1.1设二维随机变量(,)的联合概率密度函数为:试求:在时,求。解:当时,==1.2设离散型随机变量X服从几何分布:试求的特征函数,并以此求其期望与方差。解:Word格式完美整理所以:2.1袋中红球,每隔单位时间从袋中有一个白球,两个任取一球后放回,对每对应随机变量一个确定的t时取得白球如果对时取得红球如果对tetttXt3)(.维分布函数族试求这个随机过程的一2.2设随机过程,其中是常数,与是相互独立的随机变量,服从区间上的均匀分布,服从瑞利分布,其概率密度为试证明为宽平稳过程。解:(1)与无关Word格式完美整理(2),所以(3)只与时间间隔有关,所以为宽平稳过程。2.3是随机变量,且,其中设随机过程UtUtX2cos)(求:,.5)(5)(UDUE.321)方差函数)协方差函数;()均值函数;((2.4是其中,设有两个随机过程UUttYUttX,)()(32.5)(UD随机变量,且数。试求它们的互协方差函2.5,试求随机过程是两个随机变量设BAttXBA3)(,,的均值),(Tt相互独若函数和自相关函数BA,.),()(),2,0(~),4,1(~,21ttRtmUBNAXX及则且立为多少?Word格式完美整理3.1一队学生顺次等候体检。设每人体检所需的时间服从均值为2分钟的指数分布并且与其他人所需时间相互独立,则1小时内平均有多少学生接受过体检?在这1小时内最多有40名学生接受过体检的概率是多少(设学生非常多,医生不会空闲)解:令()Nt表示(0,)t时间内的体检人数,则()Nt为参数为30的poisson过程。以小时为单位。则((1))30EN。40300(30)((1)40)!kkPNek。3.2在某公共汽车起点站有两路公共汽车。乘客乘坐1,2路公共汽车的强度分别为1,2,当1路公共汽车有1N人乘坐后出发;2路公共汽车在有2N人乘坐后出发。设在0时刻两路公共汽车同时开始等候乘客到来,求(1)1路公共汽车比2路公共汽车早出发的概率表达式;(2)当1N=2N,1=2时,计算上述概率。解:法一:(1)乘坐1、2路汽车所到来的人数分别为参数为1、2的poisson过程,令它们为1()Nt、2()Nt。1NT表示1()Nt=1N的发生时刻,2NT表示2()Nt=2N的发生时刻。1111111111()exp()(1)!NNNTftttN2221222222()exp()(1)!NNNTftttN1212121221112,12|12211122212(,)(|)()exp()exp()(1)!(1)!NNNNNNNNNTTTTTfttfttftttttNNWord格式完美整理12212121112211122210012()exp()exp()(1)!(1)!NNtNNNNPTTdtttttdtNN(2)当1N=2N、1=2时,12121()()2NNNNPTTPTT法二:(1)乘车到来的人数可以看作参数为1+2的泊松过程。令1Z、2Z分别表示乘坐公共汽车1、2的相邻两乘客间到来的时间间隔。则1Z、2Z分别服从参数为1、2的指数分布,现在来求当一个乘客乘坐1路汽车后,下一位乘客还是乘坐1路汽车的概率。2122111222100()exp()exp()zpPZZdzzzdz112。故当一个乘客乘坐1路汽车后,下一位乘客乘坐2路汽车的概率为1-p212上面的概率可以理解为:在乘客到来的人数为强度1+2的泊松过程时,乘客分别以112概率乘坐公共汽车1,以212的概率乘坐公共汽车2。将乘客乘坐公共汽车1代表试验成功,那么有:121111111211212(1=()()NNNNkNkkNPC路汽车比2路汽车先出发)(2)当1N=2N、1=2时2121111111111(1=()()2222NNNkNkkkkNkNPCC路汽车比2路汽车先出发)3.3设{(),0}iNtt,(1,2,,)in是n个相互独立的Poisson过程,参数分别为Word格式完美整理i(1,2,,)in。记T为全部n个过程中,第一个事件发生的时刻。(1)求T的分布;(2)证明1{()(),0}niiNtNtt是Poisson过程,参数为1nii;(3)求当n个过程中,只有一个事件发生时,它是属于1{(),0}Ntt的概率。解:(1)记第i个过程中第一次事件发生的时刻为1it,1,2,...,in。则1min{,1,2,...,}iTtin。由1it服从指数分布,有111111{}1{}1{min{,1,2,...,}}1{,1,2,...,}1{}1{1(1)}1exp{}iiniiinntiiiPTtPTtPtintPttinPttet...