专题训练--二次函数图象及其性质含答案VIP免费

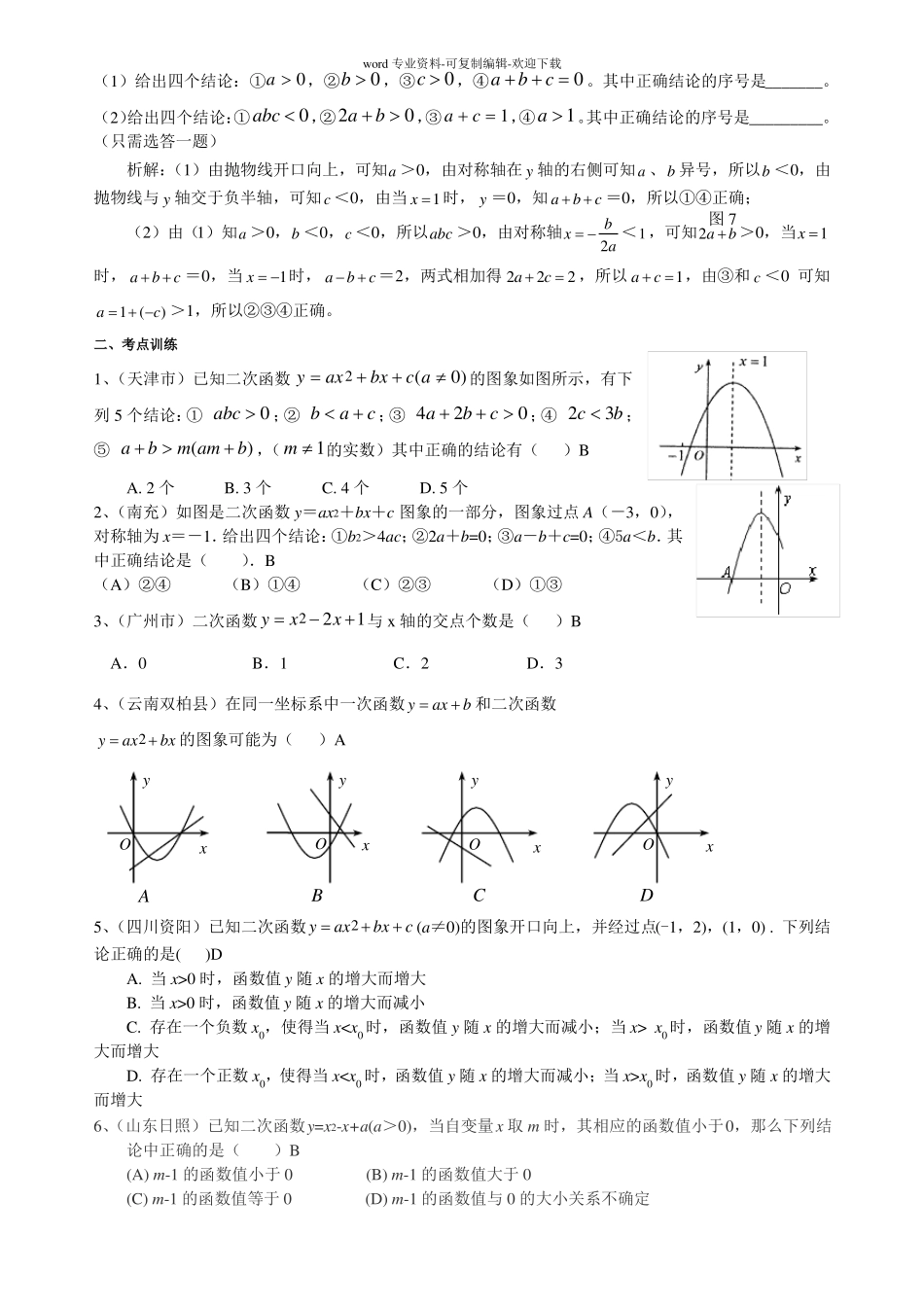
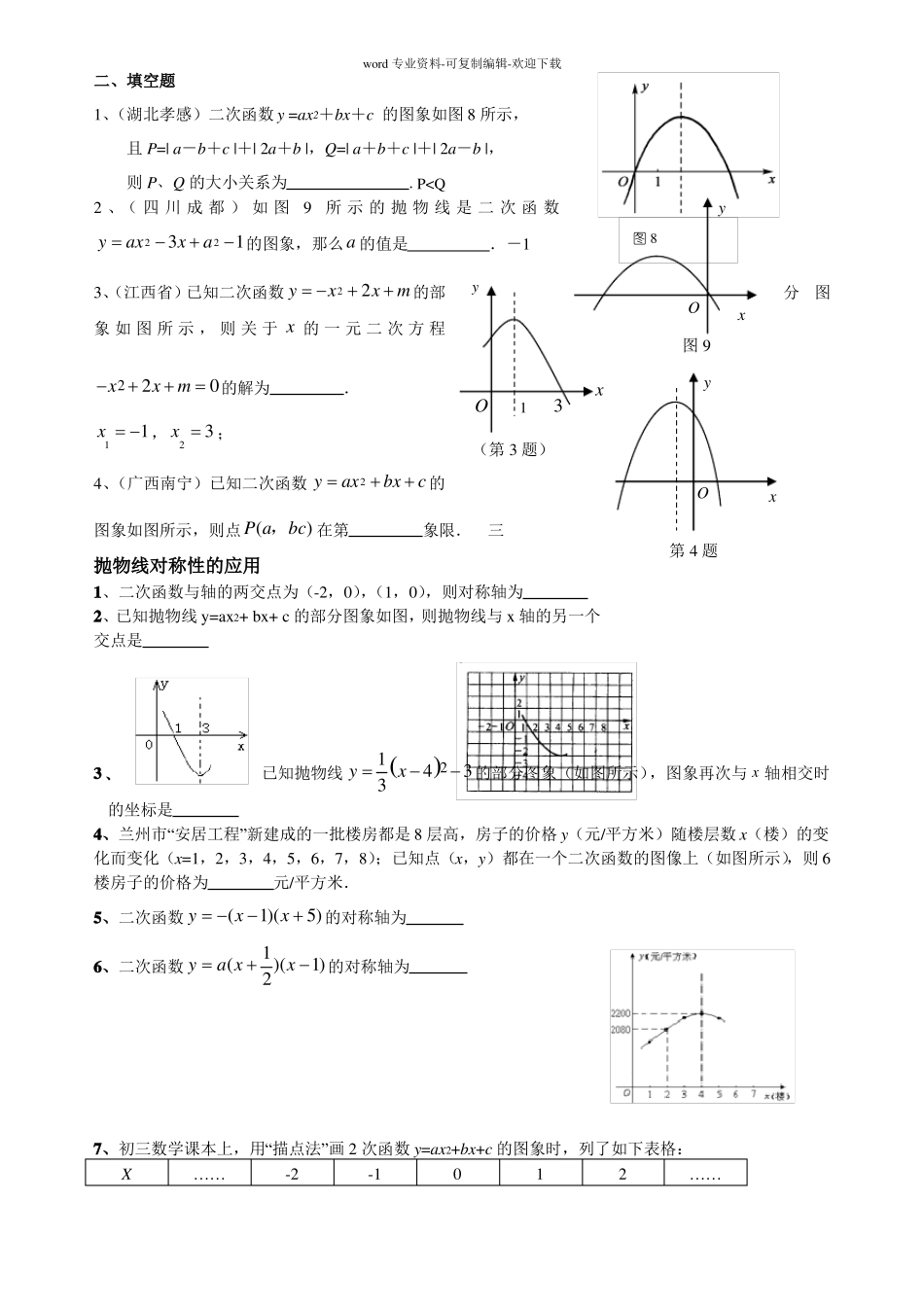
word专业资料-可复制编辑-欢迎下载专题二次函数图象及其性质二次函数的图象与系数的关系一、考点扫描二次函数yax2bxc(a0)的图象与系数的关系如下：1、a决定抛物线的开口方向：当a＞0时，抛物线开口向上；当a＜0时，抛物线开口向下。2、a决定抛物线的开口大小：a越大，则开口越小；a越小，则开口越大。3、a、b的符号决定抛物线的对称轴：当a、b同号时，对称轴在y轴的左侧；当a、b异号时，对称轴在y轴的右侧。特别地，若抛物线的对称轴是直线x＝1，则称轴是直线x＝－1，则b＝1，即b＝－2a；若抛物线的对2ab＝－1，即b＝2a．2a4、c是抛物线与y轴交点的纵坐标：当c0时，抛物线经过原点；当c＞0时，抛物线与y轴交于正半轴；当c＜0时，抛物线与y轴交于负半轴。5、b24ac决定图象与x轴是否相交：当b24ac＞0时，抛物线与x轴有两个交点；当b24ac0时，抛物线与x轴只有一个交点；当b24ac＜0时，抛物线与x轴没有交点。6、根据抛物线与x轴的位置关系可以确定b2－4ac的符号．因为当y＝0时ax2＋bx＋c＝0，所以抛物线与x轴有两个交点时，方程ax2＋bx＋c＝0有两个不相等的实数根，此时b2－4ac＞0；抛物线与x轴只有一个交点时，方程ax2＋bx＋c＝0有两个相等的实数根，此时b2－4ac＝0；抛物线与x轴没有交点时，方程ax2＋bx＋c＝0没有实数根，此时b2－4ac＜0．7、根据直线x＝1与抛物线交点的位置可以确定a＋b＋c的符号。交点在x轴上，a＋b＋c＝0；交点在第一象限a＋b＋c＞0；交点在第四象限a＋b＋c＜0．同样根据直线x＝－1与抛物线交点的位置可以确定a－b＋c的符号（自己探索）．反过来，可以由系数a、b、c的符号可确定抛物线y＝ax2＋bx＋c的大致形状．应用上述关系，便能简洁明快地根据a、b、c的符号判断抛物线的位置，或者根据抛物线的位置确定a、b、c的符号。典题精析：例1（浙江省金华市中考题）二次函数y＝ax2＋bx＋c（a≠0）的图象如图示，则下列结论：①a＞0；②c＞0；③b2－4ac＞0．其中正确的个数是（）．（A）0个（B）1个（C）2个（D）3个析解：由抛物线开口向下，得a＜0；由抛物线y轴的交点在正半轴上，0；由抛物线与x轴有两个交点，得b2－4ac＞0．正确的结论有2个，故应选C．例2（浙江省中考题）如图2，二次函数yaxbxc的图象开口向上，图象经过点（－1，2）和（1，0），且与y轴交于负半轴。2y1所O图1x得c＞word专业资料-可复制编辑-欢迎下载（1）给出四个结论：①a0，②b0，③c0，④abc0。其中正确结论的序号是_______。（2）给出四个结论：①abc0，②2ab0，③ac1，④a1。其中正确结论的序号是_________。（只需选答一题）析解：（1）由抛物线开口向上，可知a＞0，由对称轴在y轴的右侧可知a、b异号，所以b＜0，由抛物线与y轴交于负半轴，可知c＜0，由当x1时，y＝0，知abc＝0，所以①④正确；图7b（2）由（1）知a＞0，b＜0，c＜0，所以abc＞0，由对称轴x＜1，可知2ab＞0，当x12a时，abc＝0，当x1时，abc＝2，两式相加得2a2c2，所以ac1，由③和c＜0可知a1(c)＞1，所以②③④正确。二、考点训练1、（天津市）已知二次函数yaxbxc(a0)的图象如图所示，有下列5个结论：①abc0；②bac；③4a2bc0；④2c3b；⑤abm(amb)，（m1的实数）其中正确的结论有（）BA.2个B.3个C.4个D.5个2、（南充）如图是二次函数y＝ax2＋bx＋c图象的一部分，图象过点A（－3，0），对称轴为x＝－1．给出四个结论：①b2＞4ac；②2a＋b=0；③a－b＋c=0；④5a＜b．其中正确结论是（）．B（A）②④（B）①④（C）②③（D）①③3、（广州市）二次函数yx2x1与x轴的交点个数是（）BA．0B．1C．2D．34、（云南双柏县）在同一坐标系中一次函数yaxb和二次函数yax2bx的图象可能为（）A22yyyyOxOxOxOxABCD5、（四川资阳）已知二次函数yax2bxc(a≠0)的图象开口向上，并经过点(-1，2)，(1，0).下列结论正确的是()DA.当x>0时，函数值y随x的增大而增大B.当x>0时，函数值y随x的增大而减小C.存在一个负数x0，使得当xx0时，函数值y随x的增大而增大D.存在...