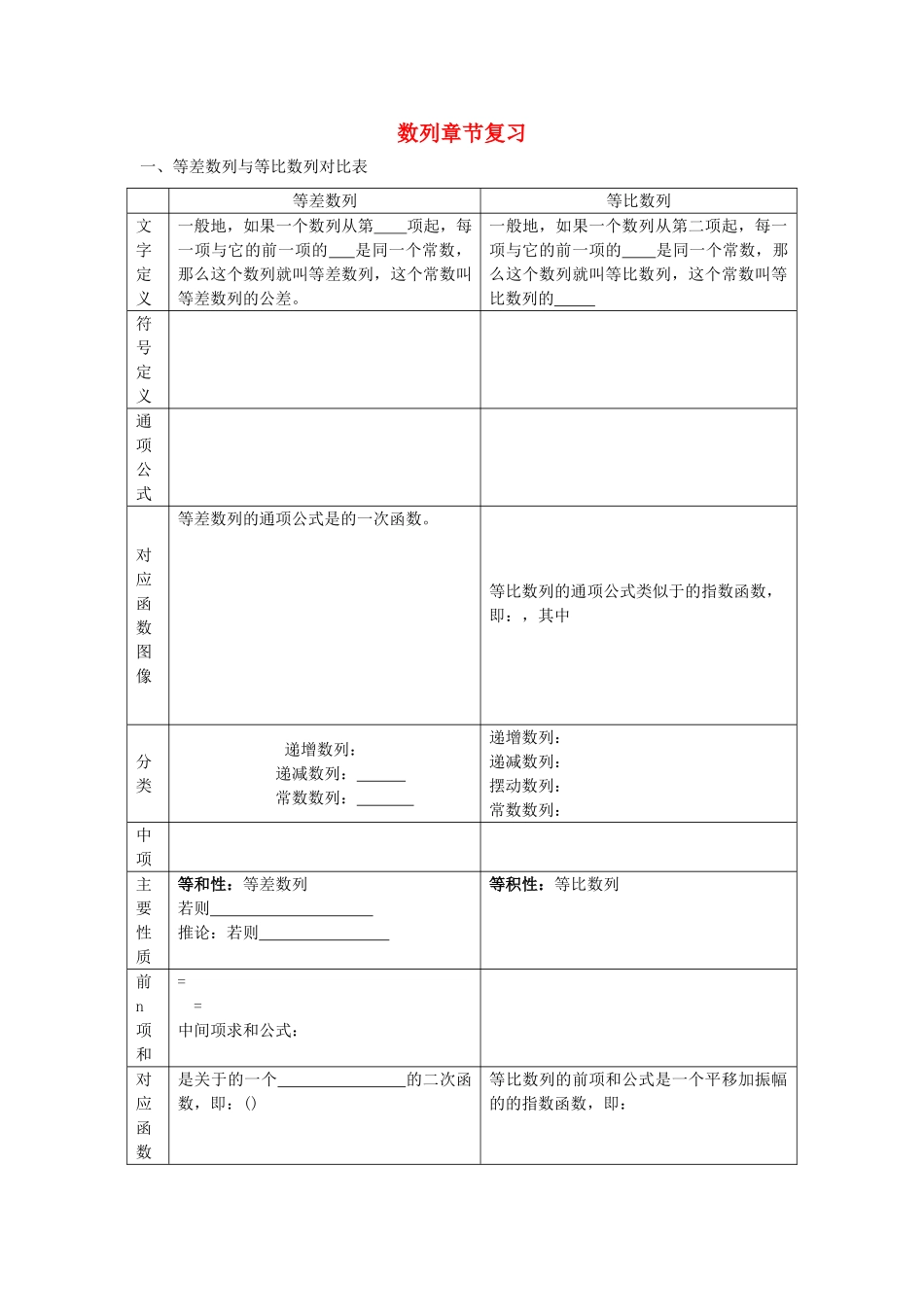
数列章节复习一、等差数列与等比数列对比表等差数列等比数列文字定义一般地,如果一个数列从第项起,每一项与它的前一项的是同一个常数,那么这个数列就叫等差数列,这个常数叫等差数列的公差。一般地,如果一个数列从第二项起,每一项与它的前一项的是同一个常数,那么这个数列就叫等比数列,这个常数叫等比数列的符号定义通项公式对应函数图像等差数列的通项公式是的一次函数。等比数列的通项公式类似于的指数函数,即:,其中分类递增数列:递减数列:常数数列:递增数列:递减数列:摆动数列:常数数列:中项主要性质等和性:等差数列若则推论:若则等积性:等比数列前n项和==中间项求和公式:对应函数是关于的一个的二次函数,即:()等比数列的前项和公式是一个平移加振幅的的指数函数,即:图像其它性质1、等差数列中连续项的和,组成的新数列是等差数列。即:等差,公差为2、从等差数列中抽取等距离的项组成的数列是一个等差数列。如:(下标成等差的子数列为数列)3、等差,则,,,是数列。4、在等差数列中,为等差数列1、等比数列中连续项的和,组成的新数列是数列。即:等比,公比为。2、从等比数列中抽取等距离的项组成的数列是一个等比数列。如:(下标成等差的子数列为数列)3、等比,则,,,是数列。其中4、等比数列中连续相同项数的积组成的新数列是等比数列。如:,,证明方法证明一个数列为等差数列的方法:1、定义法:2、中项法:证明一个数列为等比数列的方法:1、定义法:2、中项法:设元技巧三数等差:四数等差:三数等比:四数等比:联系1、若数列是等差数列,则数列是等比数列,公比为,其中是常数,是的公差。2、若数列是等比数列,且,则数列是等差数列,公差为,其中是常数且,是的公比。一、牛刀小试1、在等差数列中,若,则的值为2、(2009年广东卷文)已知等比数列的公比为正数,且·=2,=1,则=3、设成等比数列,其公比为2,则的值为4、(2010辽宁理)(6)设{an}是有正数组成的等比数列,为其前n项和。已知a2a4=1,,则5、等差数列{an}中,,为第n项,且,则取最大值时,n的值为6、等比数列中,7、已知是等比数列,an>0,且a4a6+2a5a7+a6a8=36,则a5+a7等于8、设是由正数组成的等比数列,公比,且,则__________。9、关于数列{an}有以下命题:其中正确的命题为a,b,d.(写出序号,写对但不全的给2分,有选错的不给分)10、两个等差数列则=11、已知两个等差数列{an}和{bn}的前n项和分别为An和Bn,且=,则使得为整数的正整数n的个数是12、若是等差数列,首项,,,则使前n项和成立的最大自然数n是二、例题研究例1、(1)若一个等差数列前3项的和为34,最后3项的和为146,且所有项的和为390,则这个数列有13项。(2)设数列{an}是递增等差数列,前三项的和为12,前三项的积为48,则它的首项是2。(3)设Sn是等差数列{an}的前n项和,若=,则=。解:(1)答案:13法1:设这个数列有n项 ∴∴n=13法2:设这个数列有n项 ∴∴又∴n=13(2)答案:2因为前三项和为12,∴a1+a2+a3=12,∴a2==4又a1·a2·a3=48, a2=4,∴a1·a3=12,a1+a3=8,把a1,a3作为方程的两根且a1<a3,∴x2-8x+12=0,x1=6,x2=2,∴a1=2,a3=6,∴选B.(3)答案为。例2、等差数列{an}中,Sn为其前n项和,若,求例3、(1)已知数列为等差数列,且(Ⅰ)求数列的通项公式;(Ⅱ)证明分析:(1)借助通过等差数列的定义求出数列的公差,再求出数列的通项公式,(2)求和还是要先求出数列的通项公式,再利用通项公式进行求和。解:(1)设等差数列的公差为d,由即d=1。所以即(II)证明:因为,所以例4、已知数列{an}为等差数列,公差d≠0,{an}的部分项组成下列数列:a,a,…,a,恰为等比数列,其中k1=1,k2=5,k3=17,求k1+k2+k3+…+kn.解:设{an}的首项为a1, a、a、a成等比数列,∴(a1+4d)2=a1(a1+16d).得a1=2d,q==3. a=a1+(kn-1)d,又a=a1·3n-1,∴kn=2·3n-1-1.∴k1+k2+…+kn=2(1+3+…+3n-1)-n=2×-n=3n-n-1.例5、在等差数列中,已知,.(Ⅰ)求数列的通项公式;(Ⅱ)设,求数列的前项和.(Ⅰ)在...