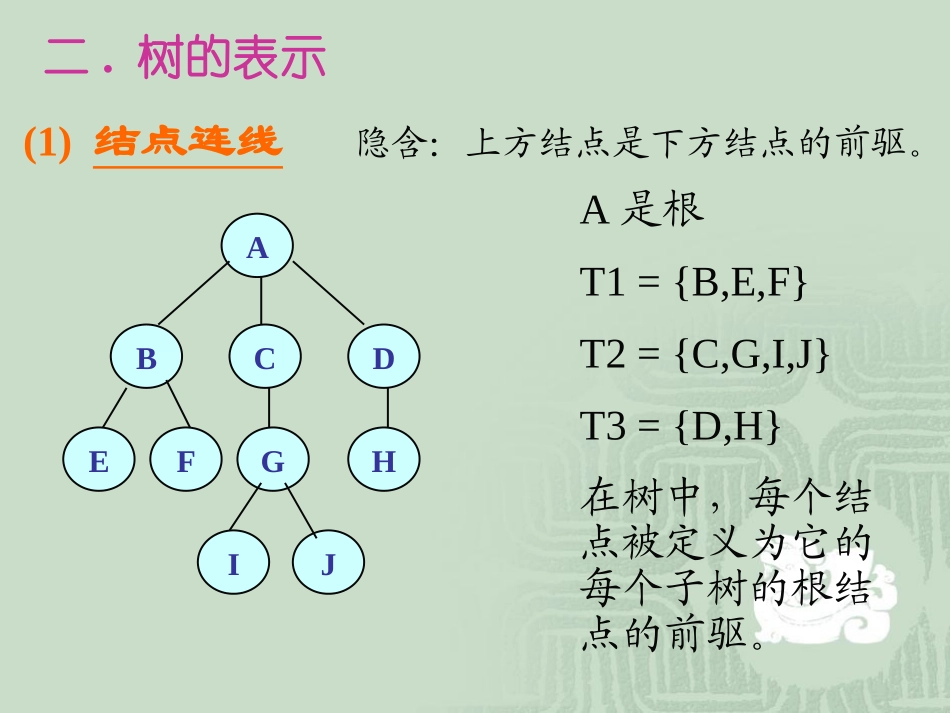
定义说明了:树是一种递归的数据结构——树中包含树。结构特点:结点间有明显层次关系。一.树的定义树是n(n≥0)个结点的有限集,n=0——空树;在一棵非空树中:(1)有且只有一个特定的结点——根结点(root);(2)当n>1,其余结点可分为m个互不相交的子集T1,T2,……,Tm,它们又是树——根结点的子树(SubTree)。例如:学校的行政关系、书的层次结构、人类的家族血缘关系、操作系统的目录、结构程序模块等。A是根T1={B,E,F}T2={C,G,I,J}T3={D,H}在树中,每个结点被定义为它的每个子树的根结点的前驱。二.树的表示(1)结点连线隐含:上方结点是下方结点的前驱。ADCBHGFEJI(2)二元组表示如下面的树可表示为:K={C,G,I,J}R={,,}JIGC(3)集合图表示法每棵树对应一个圆形,圆内包含根结点和子树。ADCBHGFEJIIJAEBDHFCG(4)凹入表示法ABEFCGIJDH每棵树的根对应着一个条形,子树的根对应着一个较短的条形。ADCBHGFEJI(5)广义表表示每棵树的根作为由子树构成的表的名字而放在表的左边。ADCBHGFEJIA(B(E,F),C(G(I,J)),D(H))(1)树的结点:包含一个数据元素及若干指向其子树的分支(2)结点的度(degree):结点拥有的子树数。(3)根结点:无前驱。(4)叶子(终端结点):度为零的结点。无后继。(5)分支结点(非终端结点)度不为零的结点。除根结点外,分支结点也称内部结点(1个前驱,多个后继)(6)树的度:树内各结点的度的最大值。三.基本术语ADCBHGFEJI(7)孩子:结点的子树的根称为该结点的孩子。相应地,该结点称为孩子的双亲。(8)兄弟:同一双亲的孩子之间互为兄弟。(9)祖先:结点的祖先是从根到该结点所经分支上的所有结点。(10)子孙:以某结点为根的子树中的任一结点都称为该结点的子孙。ADCBHGFEJI(11)结点的层次:根为第一层,根的孩子为第二层。(12)树的深度(高度):树中结点的最大层次。(13)有序树及无序树:如:是两棵不同的有序树。ACBABCADCBHGFEJI任何一棵非空树是一个二元组Tree=(root,F)其中:root被称为根结点,F被称为子树森林(14)森林:是m(m≥0)棵互不相交的树的集合ArootBEFKLCGDHIJMF四.树的基本操作(1)初始化空树:INITIATE(&T);(2)求根结点:ROOT(T);或:ROOT(x);(3)PARENT(T,x);—求当前结点的双亲结点(4)CHILD(T,x,i);求树T中结点x的第i个孩子(5)Right_sibling(T,x);—求结点x的右兄弟(6)CRT_TREE(&T,x,F);以结点x为根,以F为子树森林构造树T。设:TreeT(7)INS_TREE(&T,y,i,x);将以x为根的子树作为结点y的第i棵子树插入到树T中。(8)DEL_CHILD(&T,x,i);将树T中结点x的第i棵子树删除。(9)树的遍历:TRAVERSE(T);按某个次序依次访问树中各个结点,并使每个结点只被访问一次。(10)清除树结构:CLEAR(&T);由于树和二叉树可以相互转换,先讨论二叉树二叉树或为空树;或是由一个根结点加上两棵分别称为左子树和右子树的、互不交的二叉树组成。ABCDEFGHK根结点左子树右子树EF特点:每个结点至多只有两棵子树,子树有左右之分,其次序不能任意颠倒。二叉树的五种基本形态:N空树空树只含根结点只含根结点NNNLRR右子树为空树右子树为空树L左子树为空树左子树为空树左右子树均不为空树左右子树均不为空树(1)一棵度为2的树与一棵二叉树是否有区别?(2)有三个结点的二叉树与有三个结点的树的形态是否相同?三个结点的树:三个结点的二叉树问题:问题:特殊的二叉树特殊的二叉树:(2)完全二叉树:除最后一层外,其余各层都是满的;最后一层或者是满的,或者是右边缺少连续的若干结点。(1)满二叉树:二叉树中每一层的结点数都达到最大131027654981115141213131027654981112理想平衡树:在一棵二叉树中,若除最后一层外,其余层都是满的,则称此树是理想平衡树。满二叉树和完全二叉树是理想平衡树。但理想平衡树不一定是完全二叉树。13102765498111213性质1在二叉树的第i层上至多有2i-1个结点(i≥1)。用归纳法证明:(1)i=1时,2i-1=1,即只有一个根结点。(2)设j=i-1时命题成立,证明j=i时命题也成立。设:第i-1层上至多有2i-2个结点,在第i层上的结点数最多为:考虑:m叉树的第i层至多有个结点。mi-1(因为二叉树中每个结点的度至多为2)2i-2*2=2i-1深度为k的二叉...