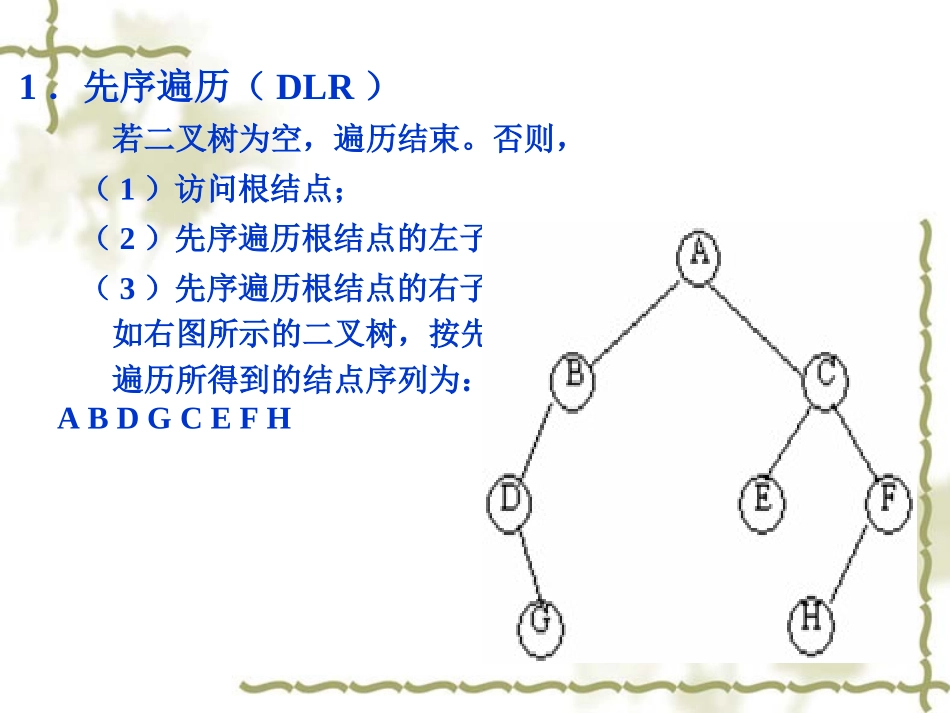
树(3)3遍历二叉树和线索二叉树3-1遍历二叉树二叉树的遍历是指按某种顺序访问二叉树中的所有结点,使得每个结点都被访问,且仅被访问一次。通过一次遍历,使二叉树中结点的非线性序列转变为线性序列。也就是说,使得遍历的结点序列之间有一个一对一的关系。由二叉树的递归定义可知,一棵二叉树由根结点(D)、根结点的左子树(L)和根结点的右子树(R)三部分组成。因此,只要依次遍历这三部分,就可以遍历整个二叉树。若以D、L、R分别表示访问根结点、遍历根结点的左子树、遍历根结点的右子树,则二叉树的遍历方式有六种不同的组合:DLR、LDR、LRD、DRL、RDL和RLD。一般限定先左后右的次序,那么只有三种遍历:DLR(根左右)、LDR(左根右)、LRD(左右根)。1.先序遍历(DLR)若二叉树为空,遍历结束。否则,(1)访问根结点;(2)先序遍历根结点的左子树;(3)先序遍历根结点的右子树。如右图所示的二叉树,按先序遍历所得到的结点序列为:ABDGCEFH2.中序遍历(LDR)若二叉树为空,遍历结束。否则,(1)中序遍历根结点的左子树;(2)访问根结点;(3)中序遍历根结点的右子树。如右图所示的二叉树,按中序遍历所得到的结点序列为:DGBAECHF3.后序遍历(LRD)若二叉树为空,遍历结束。否则,(1)后序遍历根结点的左子树;(2)后序遍历根结点的右子树。(3)访问根结点;如右图所示的二叉树,按后序遍历所得到的结点序列为:GDBEHFCA4.层次遍历按照自上而下(从根结点开始),从左到右(同一层)的顺序逐层访问二叉树上的所有结点,这样的遍历称为按层次遍历。如右图所示的二叉树,按层次遍历所得到的结果序列为:ABCDEFGH【例】有一如图所示的二叉树,求它的先序遍历、中序遍历、后序遍历和层次遍历结果。先序遍历的序列:ABDGEHCFIK中序遍历的序列:DGBHEAFKIC后序遍历的序列:GDHEBKIFCA层次遍历的序列:ABCDEFGHIKABCIKFEDHG【练习】设表达式A–B*(C+D)+E/(F+G)的二叉树表示如图所示。试写出它的先序遍历、中序遍历和后序遍历。先序遍历的结果(即前缀表达):+–A*B+CD/E+FG中序遍历的结果:A–B*C+D+E/F+G后序遍历(即后缀表达式):ABCD+*–EFG+/+A*/EF++BDC-+G3-2恢复二叉树在统一绘图软件或其它绘图软件中存在着这样的问题:如何存储一个用树表示的图形数据结构?在研制统一绘图软件系统时是用这样的办法来处理的:(1)对于用链表结构表示的图形数据结构,我们把每一个结点去掉指针项,只按结点的中序序列存储,并给出这棵树的前序(或后序)“序表”。(2)图形结构调入内存时,由中序的结点表及“序表”,形成的前序和中序数组(或后序和中序数组),恢复图形数据结构。二叉树的先序遍历是先访问根结点,然后再遍历根结点的左子树,最后遍历根结点的右子树。即在先序序列中,第一个结点必定是二叉树的根结点。中序遍历则是先遍历左子树,然后访问根结点,最后再遍历右子树。这样,根结点在中序序列中必然将中序序列分割成两个子序列,前一个子序列是根结点的左子树的中序序列,而后一个子序列是根结点的右子树的中序序列。根据这两个子序列,先由先序序列确定第一个结点为根结点;知道根结点后,按中序序列可以划分左、右子树。在先序序列中,左子树序列的第一个结点是左子树的根结点,右子序列的第一个结点是右子树的根结点。这样,就确定了二叉树的三个结点。同时,左子树和右子树的根结点又可以分别把左子序列和右子序列划分成两个子序列,如此递归下去,当取尽先序序列中的结点时,便可以恢复一棵二叉树。1.由前序和中序恢复二叉树(1)根据前序序列确定树的根(第一个结点),根据中序序列确定左子树和右子树;(2)分别找出左子树和右子树的根结点,并把左、右子树的根结点联到父(father)结点上去;(3)再对左子树和右子树按此法找根结点和左、右子树,直到子树只剩下1个结点或2个结点或空为止。【例】由下列前序序列和中序序列恢复二叉树。前序序列:ACBRSEDFMLK中序序列:RBSCEAFDLKM首先,由先序序列可知,结点A是二叉树的根结点;其次,根据中序序列,在A之前的所有结点都是根结点左子树的结点,在A之后的所有结点都是根结点右子树的结点...