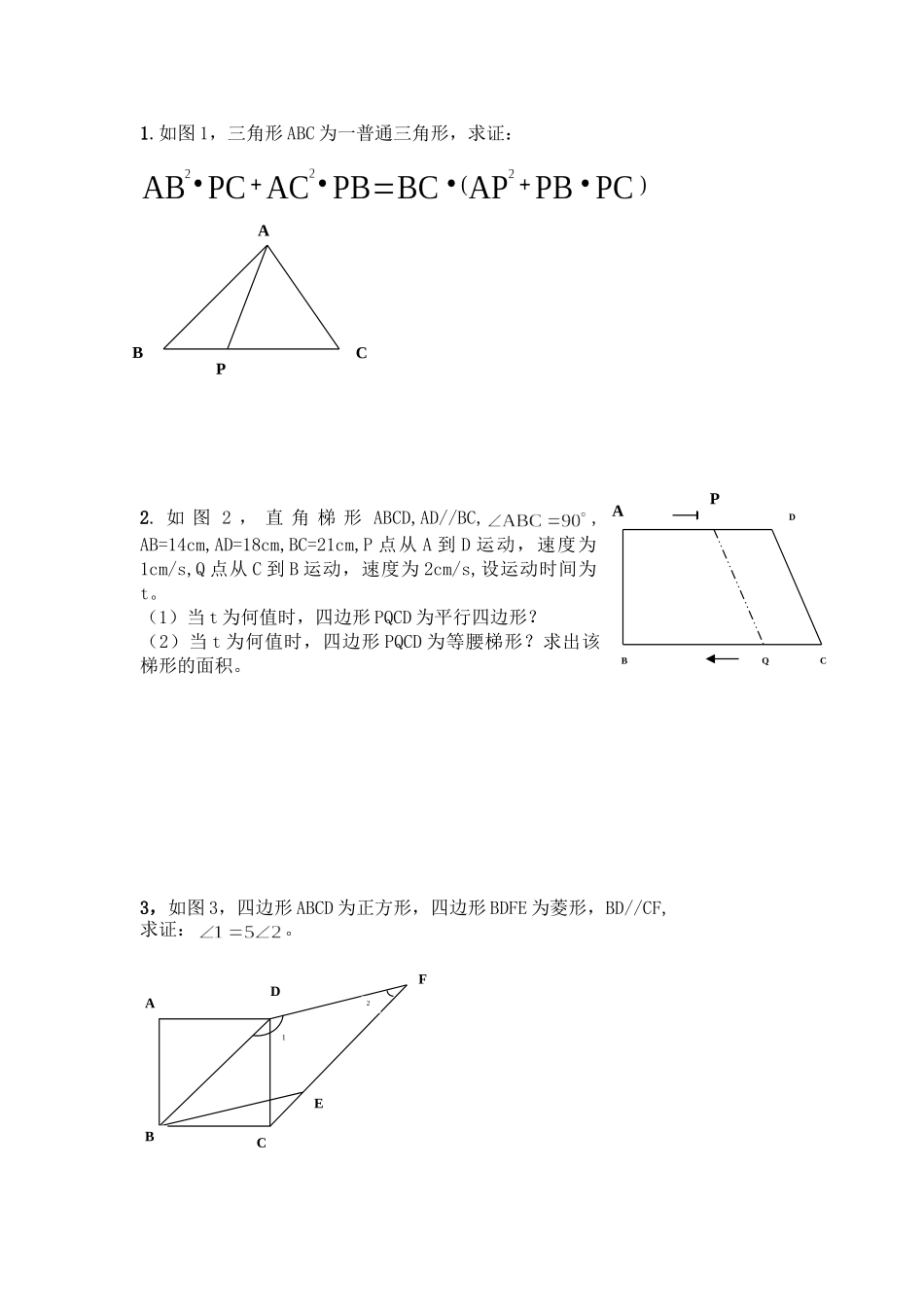
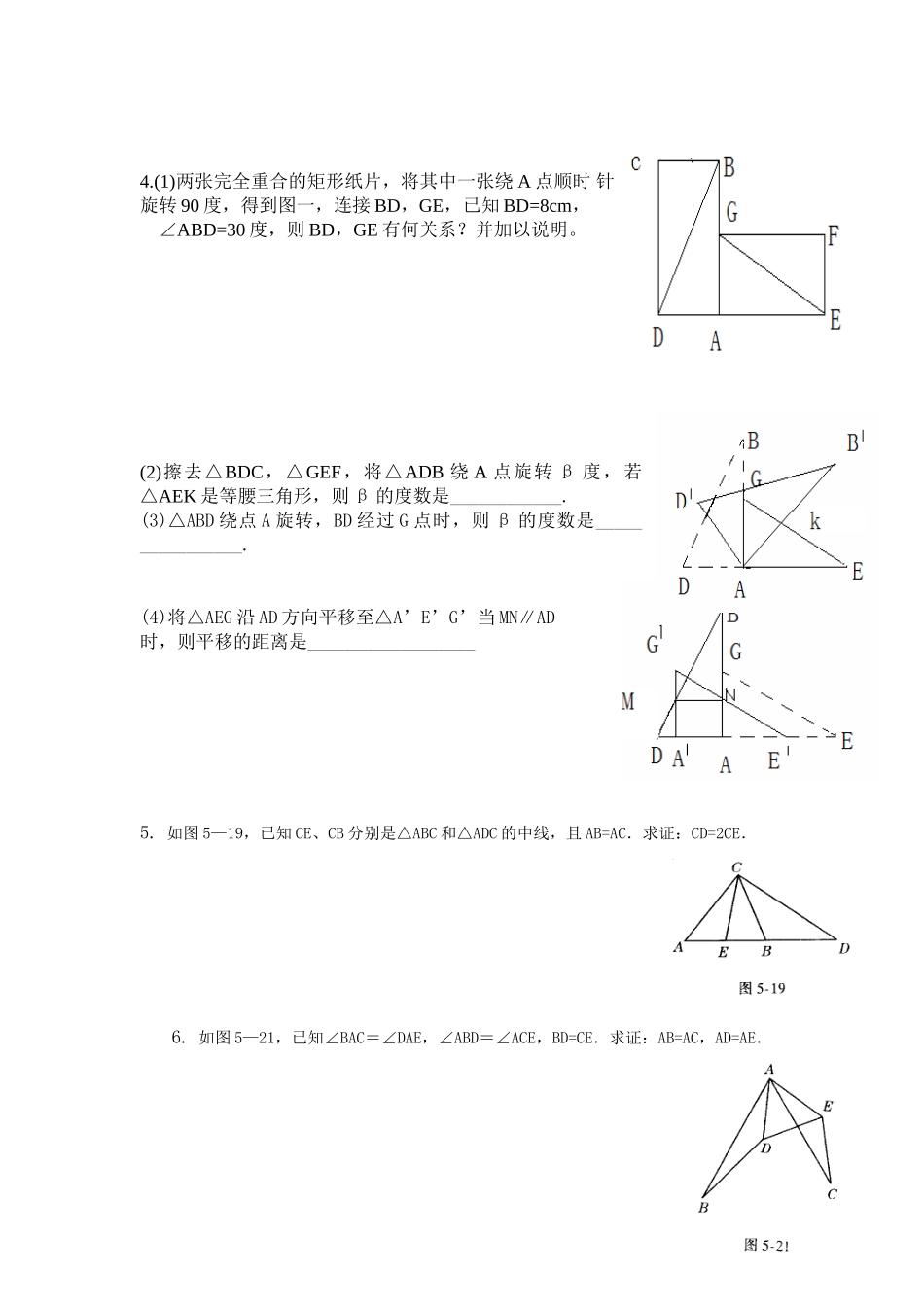
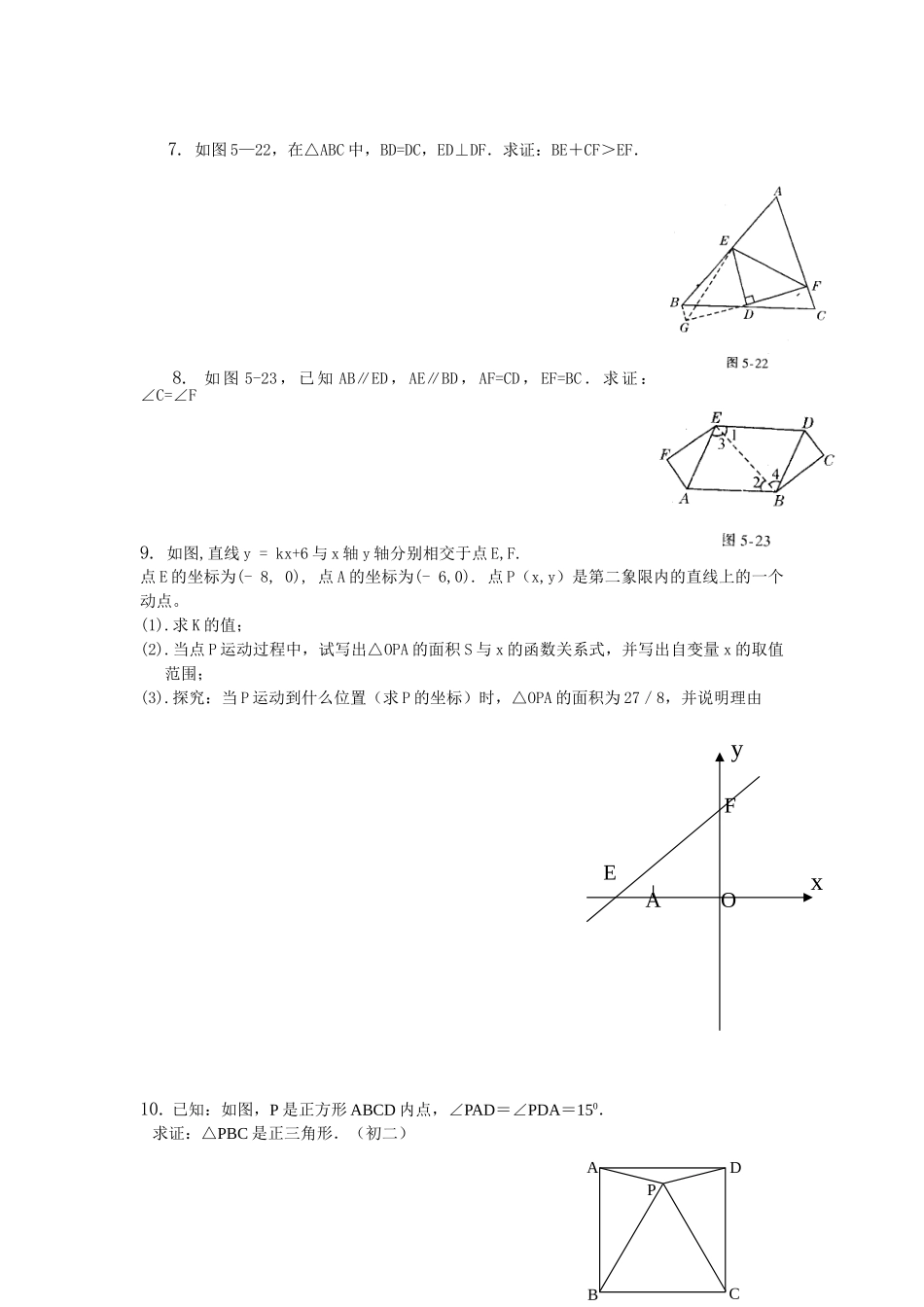
1.如图1,三角形ABC为一普通三角形,求证:2.如图2,直角梯形ABCD,AD//BC,,AB=14cm,AD=18cm,BC=21cm,P点从A到D运动,速度为1cm/s,Q点从C到B运动,速度为2cm/s,设运动时间为t。(1)当t为何值时,四边形PQCD为平行四边形?(2)当t为何值时,四边形PQCD为等腰梯形?求出该梯形的面积。3,如图3,四边形ABCD为正方形,四边形BDFE为菱形,BD//CF,求证:。APABCDEF12ADBCQAPBC4.(1)两张完全重合的矩形纸片,将其中一张绕A点顺时针旋转90度,得到图一,连接BD,GE,已知BD=8cm,∠ABD=30度,则BD,GE有何关系?并加以说明。(2)擦去△BDC,△GEF,将△ADB绕A点旋转β度,若△AEK是等腰三角形,则β的度数是____________.(3)△ABD绕点A旋转,BD经过G点时,则β的度数是________________.(4)将△AEG沿AD方向平移至△A’E’G’当MN∥AD时,则平移的距离是__________________5.如图5—19,已知CE、CB分别是△ABC和△ADC的中线,且AB=AC.求证:CD=2CE.6.如图5—21,已知∠BAC=∠DAE,∠ABD=∠ACE,BD=CE.求证:AB=AC,AD=AE.7.如图5—22,在△ABC中,BD=DC,ED⊥DF.求证:BE+CF>EF.8.如图5-23,已知AB∥ED,AE∥BD,AF=CD,EF=BC.求证:∠C=∠F9.如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标为(-8,0),点A的坐标为(-6,0).点P(x,y)是第二象限内的直线上的一个动点。(1).求K的值;(2).当点P运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;(3).探究:当P运动到什么位置(求P的坐标)时,△OPA的面积为27/8,并说明理由10.已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二)OEFAyxAPCDB11.设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.求证:PA=PF.(初二)12.已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)13.如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,求证:AC=AE+CD.14.ABC中,AB=AC,∠BAC=900,D、E在BC上,且∠DAE=450,若BD=3,CE=4求DE的长。ABEODCDFEPCBAAPCBCDABE15.已知:如图,中,,于,平分,且于,与相交于点是边的中点,连结与相交于点.(1)求证:;(2)求证:;(3)与的大小关系如何?试证明你的结论.16.△ABC中,AB=AC,将△ABC绕C点旋转至△AB′C′,连BA,,以AB,BB′为邻边作平行四边形ABB′D,连A′D:①旋转后B、C、A′在一条直线上,如图①,若∠BAC=600,则∠ADA′=____.②如图②;旋转后B、C、A′在一条直线上,若∠BAC=,则∠ADA′=________.③若将图①中的△A′B′C继续旋转至图③,使B、C、A′不在一条直线上,连AA′,试判别△ADA′的形状,并证明你的结论.17.(1)如图①,A、B、C三点在同一直线上,分别以AC,BC为边在AB的同侧作等边△ACD和等边△BCE,连接AE、BD,M、N分别为AE、BD的中点,连接CM、CN、MN.则△CMN的形状是________三角形;(2)如图②,A、B、C三点在同一直线上,分别以AC,BC为边在AB的同侧作等腰Rt△ACD和等腰Rt△BCE.∠ACD=∠BCE=90°,连接AE、BD,M、N分别为AE、BD的中点,连接CM、CN,MN.则△CMN的形状是______三角形;(3)如图③,在图②的基础上,将△BCE绕点C旋转一定的角度,其它条件不变,请将图形补充完整.试判断△CMN的形状,并说明理由.18.一次函数y=x+4与x轴、y轴分别交于A、B两点,E为OA上一动点,D为OB的延长线上一动点,且AE=BD(1)当E为OA中点时,求C点坐标.(2)当E运动到x轴正半轴上,仍有AE-BD,过E作EF⊥AB于F,ABFC的值是否变化?若不变,请求出其值;若变化,请求其变化范围.