面积与代数恒等式VIP免费

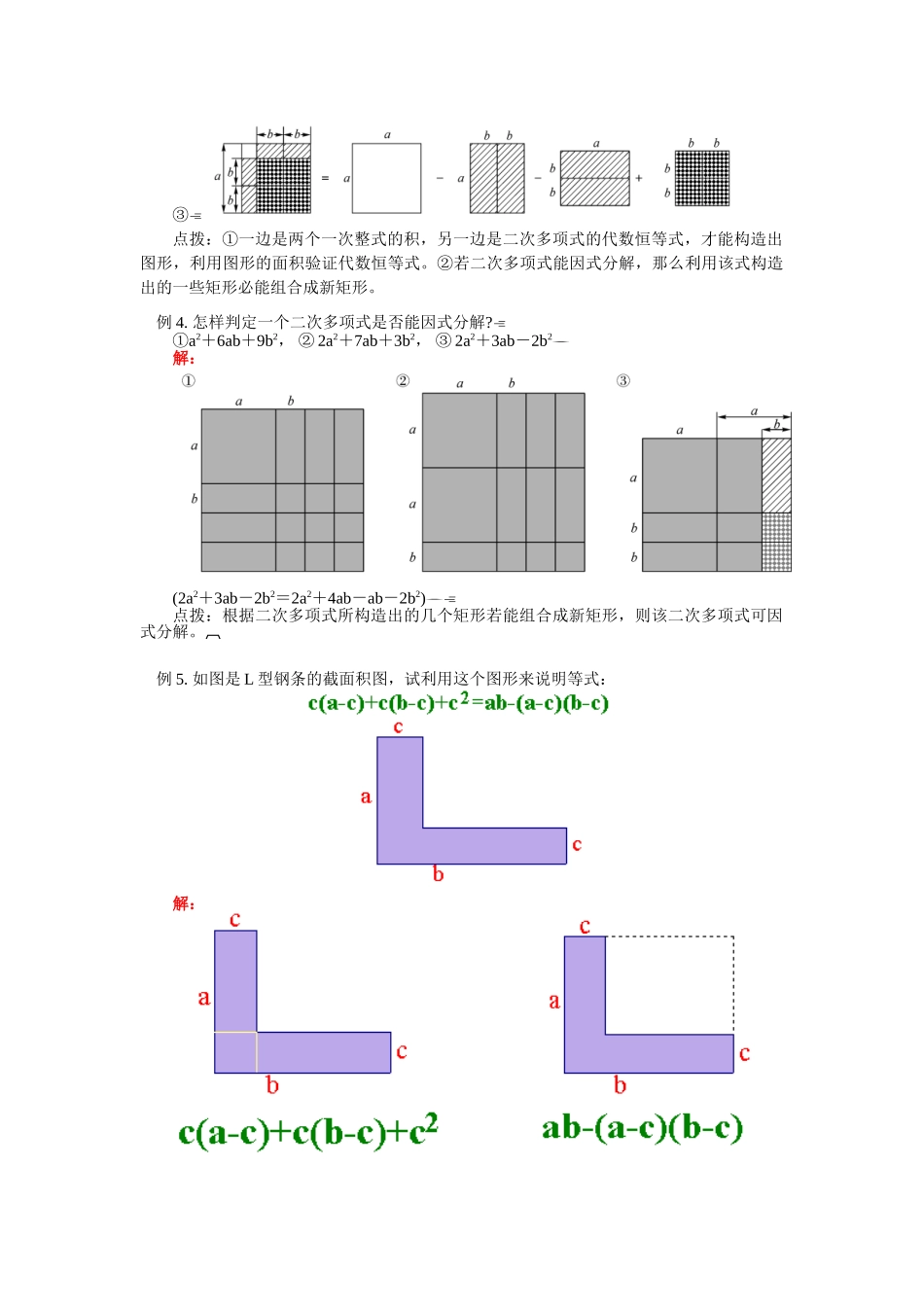
【本讲教育信息】一.教学内容：面积与代数恒等式［教学过程］一.教学目标：1.知识和技能：通过本节课的学习，会根据图形的总面积和部分面积的计算，发现和验证数学恒等式。培养学生分析问题和解决问题的能力及图形组合的想象力。2.过程和思考：通过本节课的学习，让学生通过感知、观察、实验、操作等数学活动充分感受数学的数形结合的思想。3.情感态度与价值观：在学习和探讨的过程中体验数学的探索性和创造性。通过学生间的交流与合作，培养学生在独立思考问题的基础上，能够尊重与理解他人意见。最终到达体验成功的喜悦，建立自信心。二.教学重点，难点：1.教学重点：会通过图形拼和分割来观察计算面积，并体会用图形验证代数恒等式。我们发现了这样几个特点：（1）代数恒等式我们都可以用面积的方法来加以验证它的正确性，（2）用图形的拼接我们可以发现更多的代数恒等式，我们也可以计算化简验证。用这些思想方法我们来进行练习和思考下面几个问题，相信你对此会更加感兴趣和乐于接受。一个代数恒等式如何用图形的面积来表示．2.教学难点：通过图形的拼和分割来发现新的代数恒等式，如勾股定理。【典型例题】例1.我们前面已学习了多项式相乘的有关法则及乘法公式，请利用图形的面积对它们的合理性进行验证。①乘法分配律：a(b＋c)＝ab＋ac②多项式与多项式相乘：(m＋n)(a＋b)＝ma＋mb＋na＋nb③两数和的平方：(a＋b)2＝a2＋2ab＋b2④平方差公式：(a＋b)(a－b)＝a2－b2像①②③④这种不论字母取什么值，左边恒等于右边的式子叫做代数恒等式解：①②③④点拨：①代数恒等式：一边是两个一次整式积的形式，另一边是二次多项式。②图形：都是由几个矩形组合成一个新矩形。二次恒等式式图形面积的不同表达形图形根据式的几何意义构造图形例2.观察下列图形，计算阴影部分的面积，并用面积的不同表达形式写出相应的代数恒等式。解：(a＋b)2－(a－b)2＝4ab4a2－b2＝(2a＋b)(2a－b)例3.请你根据代数恒等式：①(a＋b)(a＋2b)＝a2＋3ab＋2b2，②(a＋b)(a－2b)＝a2－ab－2b2，③(a－2b)2＝a2－4ab＋4b2的特点，构造出图形，利用图形的面积来说明其正确性。解：（1）略②③点拨：①一边是两个一次整式的积，另一边是二次多项式的代数恒等式，才能构造出图形，利用图形的面积验证代数恒等式。②若二次多项式能因式分解，那么利用该式构造出的一些矩形必能组合成新矩形。例4.怎样判定一个二次多项式是否能因式分解?①a2＋6ab＋9b2，②2a2＋7ab＋3b2，③2a2＋3ab－2b2解：(2a2＋3ab－2b2＝2a2＋4ab－ab－2b2)点拨：根据二次多项式所构造出的几个矩形若能组合成新矩形，则该二次多项式可因式分解。例5.如图是L型钢条的截面积图，试利用这个图形来说明等式：解：例6.你能用4张直角三角形纸片拼成一个正方形吗？动手试一试。用直角三角形纸片你还能拼出其他图形来说明恒等式c2＝a2＋b2的正确性吗？解：根据大正方形的面积写出一个代数恒等式：c2＝4)(2ba1/2ab，即c2＝a2＋b2，这就是直角三角形三边之间的关系，即勾股定理。它有很多证明方法。【模拟试题】1.选择题：（1）()aamn5·＝（）A.amn5B.amn5C.amn5D.amn5（2）下列运算正确的是（）A.aaa459B.aaaa33333··C.236459aaa×D.()aa347（3）()()51323519971997×（）A.－1B.1C.0D.1997（4）设()()535322ababA，则A＝（）A.30abB.60abC.15abD.12ab（5）用科学记数方法表示0.0000907，得（）A.907104.×B.907105.×C.907106.×D.907107.×（6）已知xyxy53，，则xy22＝（）A.25B.－25C.19D.－19（7）已知xxab35，，则xab32＝（）A.2725B.910C.35D.52（8）一个正方形的边长增加2cm，面积相应增加了322cm，则这个正方形的边长为（）A.6cmB.5cmC.8cmD.7cm2.填空题：（1）()()aa5423·＝_________。（2）()an2＝_________。（3）设41212xmx是一个完全平方式，则m＝_________。（4）已知xx15，那么xx331＝_________。（5）计算：()ab3＝_________。（6）方程()()()()x...