理力答案_第四章VIP免费

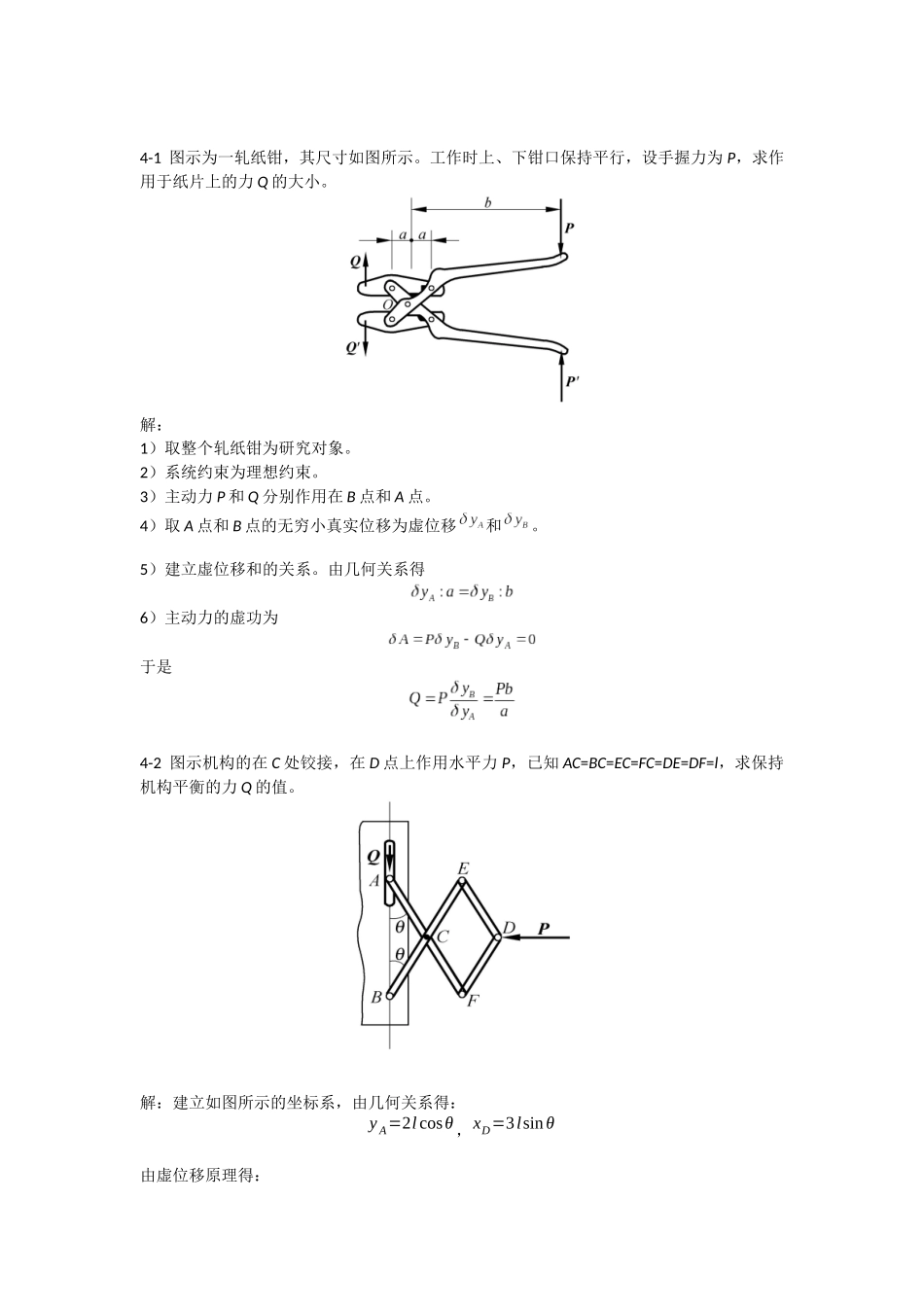
4-1图示为一轧纸钳，其尺寸如图所示。工作时上、下钳口保持平行，设手握力为P，求作用于纸片上的力Q的大小。解：1）取整个轧纸钳为研究对象。2）系统约束为理想约束。3）主动力P和Q分别作用在B点和A点。4）取A点和B点的无穷小真实位移为虚位移和。5）建立虚位移和的关系。由几何关系得6）主动力的虚功为于是4-2图示机构的在C处铰接，在D点上作用水平力P，已知AC=BC=EC=FC=DE=DF=l，求保持机构平衡的力Q的值。解：建立如图所示的坐标系，由几何关系得：yA=2lcosθ，xD=3lsinθ由虚位移原理得：QδyA+PδxD=0所以：Q=32Pctgθ4-3用滑轮机构将两物体A和B悬挂如图，并设物体B保持水平。如绳和滑轮的重量不计，求两物体平衡时，重量PA和PB的关系。解：取物块A、B为研究对象。约束为理想约束。由虚位移原理可得：PBδrB+PAδrA=0由如图所示的滑轮组可得虚位移关系为：−2δrB:δrA=2:5即：δrA=−5δrB所以：PB=5PA4-4反平行四边形机构ABCD中的杆AB、CD和BC用铰链B和C互相连接，同时又用铰链A和D连在机架AD上。在杆CD的铰链C处作用着水平力FC。在铰链B沿垂直于杆AB的方向作用有力FB，机构在图示位置处于平衡。设，，∠ABC=∠ADC=90°，∠DCB=30°。求FB的大小。xDrFFyBr解：根据题意，选三根杆组成的整体为研究对象，约束均为理想约束，主动力为FCF及B。质系平衡，则由虚位移原理，有又由运动学知识，(δrC/δrB1)=(vC/vB1)=1/（cosπ/3）其中δrB1v及B1是沿CB杆方向的分量。联立上述两式可得，FB=2FC4-5滑套D套在光滑直杆AB上，并带动CD杆在铅垂滑道上滑动，如图所示。已知当时，弹簧等于原长，且弹簧系数为5kN/m。若系统的自重不计，求在任意位置θ角平衡时，在AB杆上应加多大力偶矩M。解：如图所示，以A为原点建立坐标系。则D点坐标：对上式进行变分可得：(1)此时弹簧的弹力为：(2)以杆AB、滑套D和杆CD为研究对象，约束为理想约束。将弹簧去除，代之以作用在D和B上的弹簧力。弹簧力在上所做的虚功为零，在上做的虚功为，利用虚位移原理有：(3)将(1)式代入得：由的任意性可得：将(2)式代入，并由可得：4-6两等长杆AB与BC在B点用铰链接，又在杆的D和E两点连一弹簧，如图所示。弹簧系数为k，当距离AC等于a时，弹簧的拉力为零。如在C点作用一水平力F，杆系处于平衡。设AB=l，BD=b，杆重及摩擦略去不计，求距离AC之值。解：解除弹簧DE的约束，代之以约束反力和。因为当AC等于a时，弹簧的拉力为零，从而当AC等于时，弹簧弹力：()bTxakl由约束知：（1）主动力的虚功为：CxT-TCxT-T（2）将（1）代入（2）得到：得到距离AC为：4-7在图示机构中，AB与CD长均为a=300cm，在E处以铰链连接，BE＝DE＝a/3，AB与BF在B处以铰链连接，D处为一光滑套筒，C处为小滚轮，弹簧刚度系数为1.8kN/m,且当时，弹簧具有原长，求当在B处作用载荷P=1.2kN时,系统的平衡位置。解：将弹簧解除，代之以弹簧力F，弹簧力的大小为：(1)利用虚功原理解本题。以A为原点建立坐标系，如图所示，则：(2)其中，l是BF的长度。对(2)式变分可得：(3)主动力为：，则根据虚功原理可得：由于的任意性，可得：xyFFxyFF即：将(1)带入可得：所以：4-8在曲柄OA上作用力矩为M=6N⋅m的力偶。OA=150mm，OO1=200mm,O1B=500mm,BC=780mm,略去摩擦及自重。当OA⊥OO1时（如图所示），为了使机构处于平衡，求作用在滑块C上的水平力P。解：如图，OA杆速度为vA=vAe+vAr,其中vAe=vBAO1BO1=vAsinθ对BC杆，有,其中,,由以上式子可得则A点的虚位移rA与滑块C的虚位移rC的关系同速度之间的关系，即vAvBvCvAevArBECO1由虚位移原理，代入rA与rC的关系得P=125N.4-9两相同的均质杆，长度均为l，质量均匀为m，其上作用力偶如图。试求在平衡状态时，杆与水平线之间的夹角θ1，θ2。解：假设上面杆的质心为A点，下面质心为B点。假设θ2不动，θ1有一个小的转角δθ1，那么δrB=2δrA=lδθ1，那么两根杆所做的功为32mglcosθ1δθ1而力偶所做的功为：Mδθ1而根据虚位移原理，(M−32mglcosθ1)δθ1=0∴M−32mglcosθ1=0θ1=arccos2M3mgl现假设θ1不动，θ2有一个小的转角δθ2，那么δrB=12lδθ2，δrA=0，两根杆所做的...