第七章 曲线与曲面VIP免费

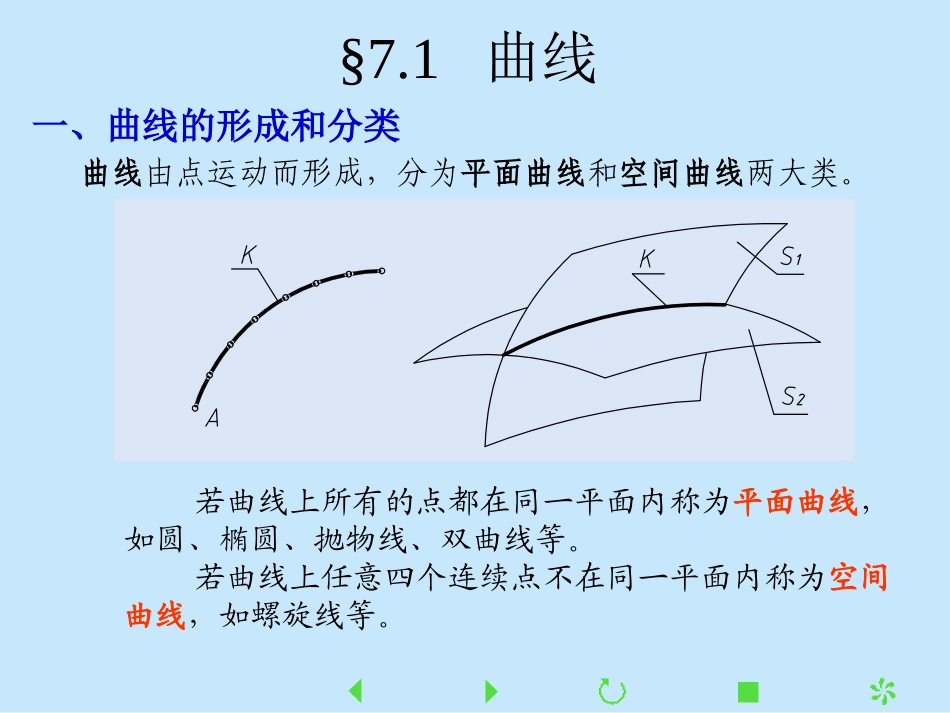
第七章曲线与曲面§7.1曲线§7.2曲面概述§7.3回转面§7.4非回转直纹曲面§7.5平螺旋面曲线与曲面和直线与平面一样，也是构成形体表面的几何元素。本章主要介绍常用曲线与曲面的形成规律、几何性质及表达方法。§7.1曲线一、曲线的形成和分类曲线由点运动而形成，分为平面曲线和空间曲线两大类。若曲线上所有的点都在同一平面内称为平面曲线，如圆、椭圆、抛物线、双曲线等。若曲线上任意四个连续点不在同一平面内称为空间曲线，如螺旋线等。二、曲线的投影特性因为曲线是由点的运动而形成的，所以只要画出曲线上一系列点的投影，并将各投影一次光滑地连接起来，就可以得到曲线的投影。（1）平面曲线的投影在一般情况下仍为平面曲线，平面曲线上点的投影必定在平面曲线的同面投影上。（2）平面曲线所在平面垂直投影面时,曲线在该投影面上的投影为一直线。（3）平面曲线所在平面平行投影时，曲线在该投影面上的投影反映实形。1.平面曲线2.空间曲线空间曲线的投影在任何情况下都是曲线，并且不可能反映曲线的实形。曲线的割线、切线CDEFefcdkg1gG1GK曲线的割线曲线的切线曲线的切线曲线的重影点LMl(m)平面曲线的投影和实长X1V1HO1113141516171b1a121将曲线段分成若干小段，每小段曲线段的端点用直线连接起来，采用以直代曲法求解。XadOcbYd"a"(o"b")c"三、圆的投影o1作圆的两面投影a1b1d1c1X1badc2143R(2')1'4'(3')41312111y1y1y1y1y2y2y2y2MM●MM1●导程导程圆柱螺旋线圆柱螺旋线OOOO四、圆柱螺旋线1.螺旋线的形成当一个动点M沿着一直线等速移动，而该直线同时绕与它平行的一轴线等速旋转，动点的轨迹是一根圆柱螺旋线。直线旋转时形成一个圆柱面，圆柱螺旋线是该圆柱面上的一根空间曲线。当直线旋转一周，回到原来位置时，动点M移到位置M1，在该直线上移动的距离MM1，称为距或导程，以Ph标记。只要给出圆柱的直径Φ、螺旋线的导程Ph以及动点移动的方向，就能确定该圆柱螺旋线的形状。§7.2曲面的形成与分类曲面为一动线在空间连续运动的轨迹。该动线称为母线，母线的每一位置称为该曲面上的素线，无限接近的相邻两素线称为连续两素线，用来控制母线运动的一些点、线、面称为导点，导线和导面。P导平面曲导线直导线母线形成曲面的母线可以是直线也可以是曲线。1.根据母线的不同可以把曲面分为直纹曲面（直线面）和双向曲面（曲线面）两大类。直纹曲面（直线面）：凡是可以由直母线运动而形成的曲面；双向曲面（曲线面）：只能由曲母线运动而形成的曲面。2.曲面又可根据其是否能无变形地展开成一平面而分为可展曲面与不可展曲面。可展曲面：曲面上连续两直素线是彼此相交或平行的（即位于同一平面上），则该曲面为可展曲面；不可展曲面：曲面上连续两直素线是彼此交叉的（即不位于同一平面上），则该曲面为不可展曲面。注：双向曲面（曲线面）都是不可展曲面，直纹曲面（直线面）中有的是可展的，有的是不可展的。3.根据母线运动方式的不同，曲面又可分为回转面和非回转面：回转面：由母线绕一轴线旋转而形成的曲面；非回转面：由母线根据其他约束条件运动而形成的曲面。§7.3回转面某由直母线或曲母线绕一轴线旋转而形成的曲面，称为回转面。曲母线绕绕同一平面内的轴线旋转时，母线上任一点（如点A）的运动轨迹都是一个垂直于轴线的圆，称为纬圆（N）。最大的纬圆称为赤道圆（P），最小的纬圆称为颈圆（Q）。§7.4非回转直纹曲面锥面锥面直母线M沿着一曲导线L移动，并始终通过一定点S而形成锥面。定点S称为锥顶。曲导线L可以是平面曲线或空间曲线；可以是闭合的，也可以不闭合的。锥面相邻两素线是相交直线。柱面柱面直母线M沿着曲导线L移动，并始终平行于一直导线K而形成柱面。柱面相邻两素线是平行直线。画柱面的投影图时，必须画出曲导线L，直导线K和一系列素线的投影。双曲抛物面双曲抛物面由直母线沿着两交叉直导线移动，并始终平行于一个导平面而形成双曲抛物面。图示的双曲抛物面，直母线是BD，交叉直导线是AB和CD。所有素线都平行于铅垂导平面P。双曲抛物面的相邻两素线是交叉直线。锥状面锥状面直母线沿着一根直导线和一根曲导线移动，并始终平行于一个导平面而形成锥状...