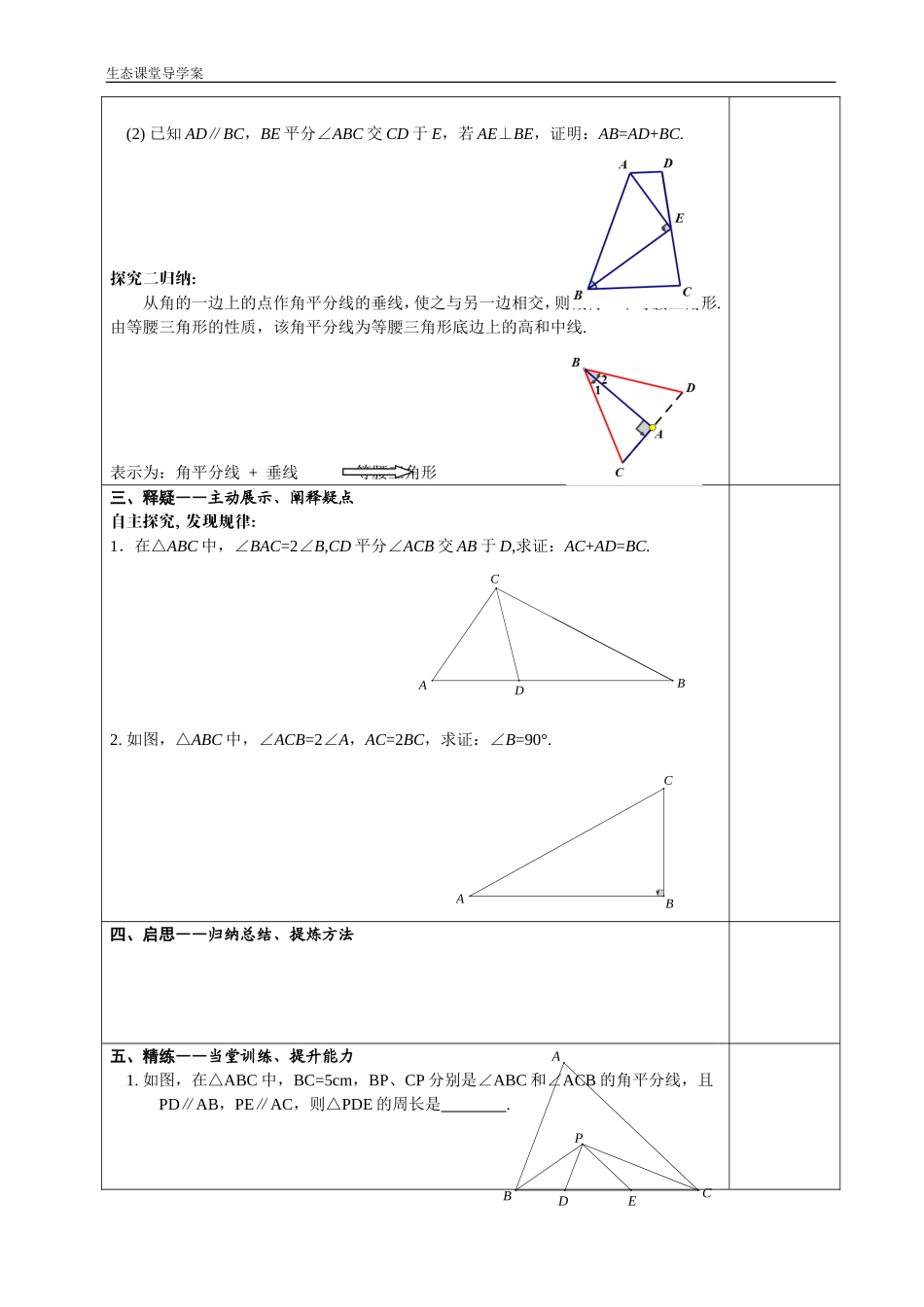
生态课堂导学案等腰三角形专题构建等腰三角形(第1课时)教与导学的过程要点归纳学习目标:进一步熟练运用等腰三角形的性质和判定,体验轴对称的特征,发展空间观念,根据已知条件构建等腰三角形,探索归纳构造等腰三角形的最佳条件.培养自主探究意识。学习重点:等腰三角形的构建.学习难点:灵活应用已知条件构建等腰三角形.一、导疑――情境导入、提出疑问1.等腰三角形有哪些性质?2.如何判断一个三角形是等腰三角形?二、引探――自主学习、探究问题探究一:(1)△ABC中,AD平分∠BAC,BD⊥AD,DE∥AC.求证:DE=AB.(2)在△ABC中,AB≠AC,DE=EC,∠1=∠2,DF∥BA,求证:DF=AC.探究一归纳:有角平分线时,常过角平分线上一点作角一边的平行线,从而构造等腰三角形.表示为:角平分线+平行线等腰三角形探究二:(1)在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE,AB=5cm,AC=12cm.试求出BE的长.BCABCA生态课堂导学案(2)已知AD∥BC,BE平分∠ABC交CD于E,若AE⊥BE,证明:AB=AD+BC.探究二归纳:从角的一边上的点作角平分线的垂线,使之与另一边相交,则截得一个等腰三角形.由等腰三角形的性质,该角平分线为等腰三角形底边上的高和中线.表示为:角平分线+垂线等腰三角形三、释疑――主动展示、阐释疑点自主探究,发现规律:1.在△ABC中,∠BAC=2∠B,CD平分∠ACB交AB于D,求证:AC+AD=BC.2.如图,△ABC中,∠ACB=2∠A,AC=2BC,求证:∠B=90°.四、启思――归纳总结、提炼方法五、精练――当堂训练、提升能力1.如图,在△ABC中,BC=5cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是.EDPBCADCABABC生态课堂导学案2.(1)如图,在△ABC中,BD=CD,∠1=∠2,求证:AB=AC.(2)如图,BD=CD,∠1=∠2,此时EB=AC是否成立?说明理由.3.如图,在△ABC中,AC=BC,∠ACB=90°,D是AC上的一点,AE⊥BD交BD的延长线于E,且AE=BD.求证:BD是∠ABC的角平分线.12DBCA12EDBCAEACBD