第七章 挡土结构物上的土压力VIP免费

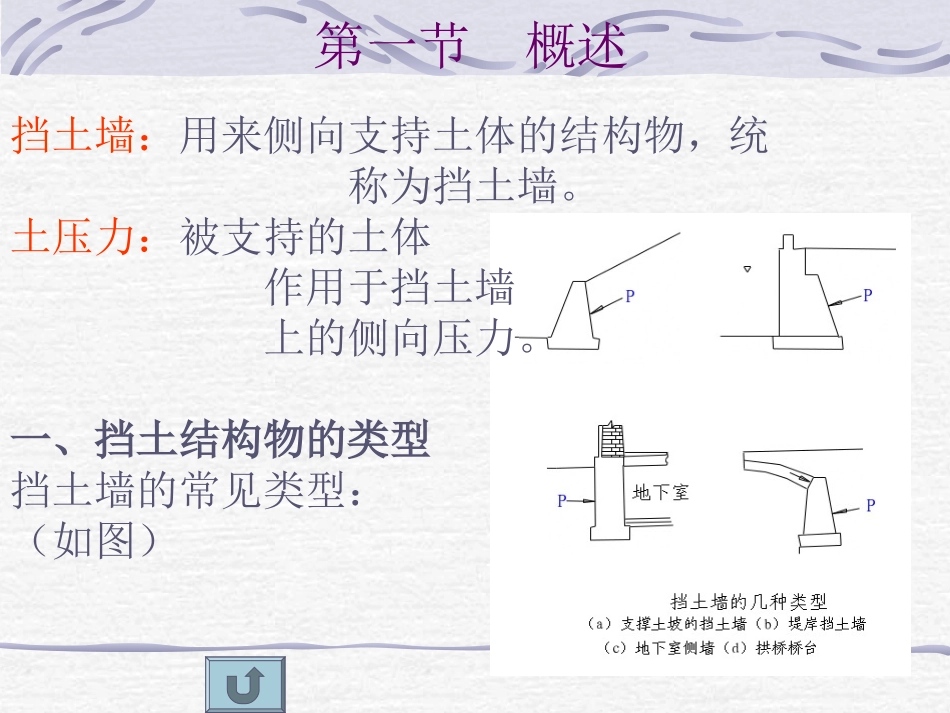
第七章挡土结构物上的土压力第一节概述第二节静止土压力计算第三节朗肯土压力理论第四节库伦土压力理论第五节若干问题的讨论第一节概述挡土墙：用来侧向支持土体的结构物，统称为挡土墙。土压力：被支持的土体作用于挡土墙上的侧向压力。一、挡土结构物的类型挡土墙的常见类型：（如图）按常用的结构形式分：重力式、悬壁式、扶臂式、锚式挡土墙按刚度及位移方式分：刚性挡土墙、柔性挡土墙、临时支撑二、墙体位移与土压力类型墙体位移的方向和位移量决定着所产生的土压力性质和土压力大小。太沙基的模型试验结果三种土压力的关系：静止土压力对应于图中A点墙位移为0，墙后土体处于弹性平衡状态主动土压力对应于图中B点墙向离开填土的方向位移，墙后土体处于主动极限平衡状态被动土压力对应于图中C点墙向填土的方向位移，墙后土体处于被动极限平衡状态PPaa0.1H绕墙顶转动0.05H粘土主动平移0.004H绕墙趾转动0.004H挡土墙在土压力作用下，不向任何方向发生位移和转动时，墙后土体处于弹性平衡状态，作用在墙背上的土压力称为静止土压力。当挡土墙沿墙趾向离开填土方向转动或平行移动，且位移达到一定量时，墙后土体达到主动极限平衡状态，填土中开始出现滑动面，这时在挡土墙上的土压力称为主动土压力。当挡土墙在外力作用下向墙背填土方向转动或平行移动时，土压力逐渐增大，当位移达到一定量时，潜在滑动面上的剪应力等于土的抗剪强度，墙后土体达到被动极限平衡状态，填土内开始出现滑动面，这时作用在挡土墙上的土压力增加至最大，称为被动土压力。第二节静止土压力计算hvhvh=p0zzzH(a)(b)静止土压力强度（p0）可按半空间直线变形体在土的自重作用下无侧向变形时的水平侧向应力h来计算。下图表示半无限土体中深度为z处土单元的应力状态：设想用一挡土墙代替单元体左侧的土体，挡土墙墙背光滑，则墙后土体的应力状态并没有变化，仍处于侧限应力状态。竖向应力为自重应力：z=z水平向应力为原来土体内部应力变成土对墙的应力，即为静止土压力强度p0：p0=h=K0zK0HH3P0(c)zpf=c+tg(d)h=p0zzH(b)静止土压力沿墙高呈三角形分布，作用于墙背面单位长度上的总静止土压力（P0）：P0的作用点位于墙底面往上1/3H处，单位[kN/m]。（d）图是处在静止土压力状态下的土单元的应力摩尔圆，可以看出，这种应力状态离破坏包线很远，属于弹性平衡应力状态。2000021HKdzpPH第三节朗肯土压力理论一、基本原理朗肯理论的基本假设：1.墙本身是刚性的，不考虑墙身的变形；2.墙后填土延伸到无限远处，填土表面水平（=0）；3.墙背垂直光滑（墙与垂向夹角=0，墙与土的摩擦角=0）。1857年英国学者朗肯（Rankine）从研究弹性半空间体内的应力状态，根据土的极限平衡理论，得出计算土压力的方法，又称极限应力法。表面水平的均质弹性半空间体的极限平衡状态图土体内每一竖直面都是对称面，地面下深度z处的M点在自重作用下，垂直截面和水平截面上的剪应力均为零，该点处于弹性平衡状态（静止土压力状态），其大小为：zKzhv031用1、、3作摩尔应力圆，如左图所示。其中3（h）既为静止土压力强度。hvhvz(a)zpf=c+tg(d)二、主动土压力的计算用1，3作摩尔应力圆，如图中应力圆I所示。使挡土墙向左方移动，则右半部分土体有伸张的趋势，此时竖向应力v不变，墙面的法向应力h减小。v、h仍为大小主应力。当挡土墙的位移使得h减小到土体已达到极限平衡状态时，则h减小到最低限值pa，即为所求的朗肯主动土压力强度。处。作用点位置在墙高）（总的土压力为：）（主动土压力强度为：对于无粘性...