潮州市金山中学高三数学5月联考（三模）试题 文-人教版高三数学试题VIP免费

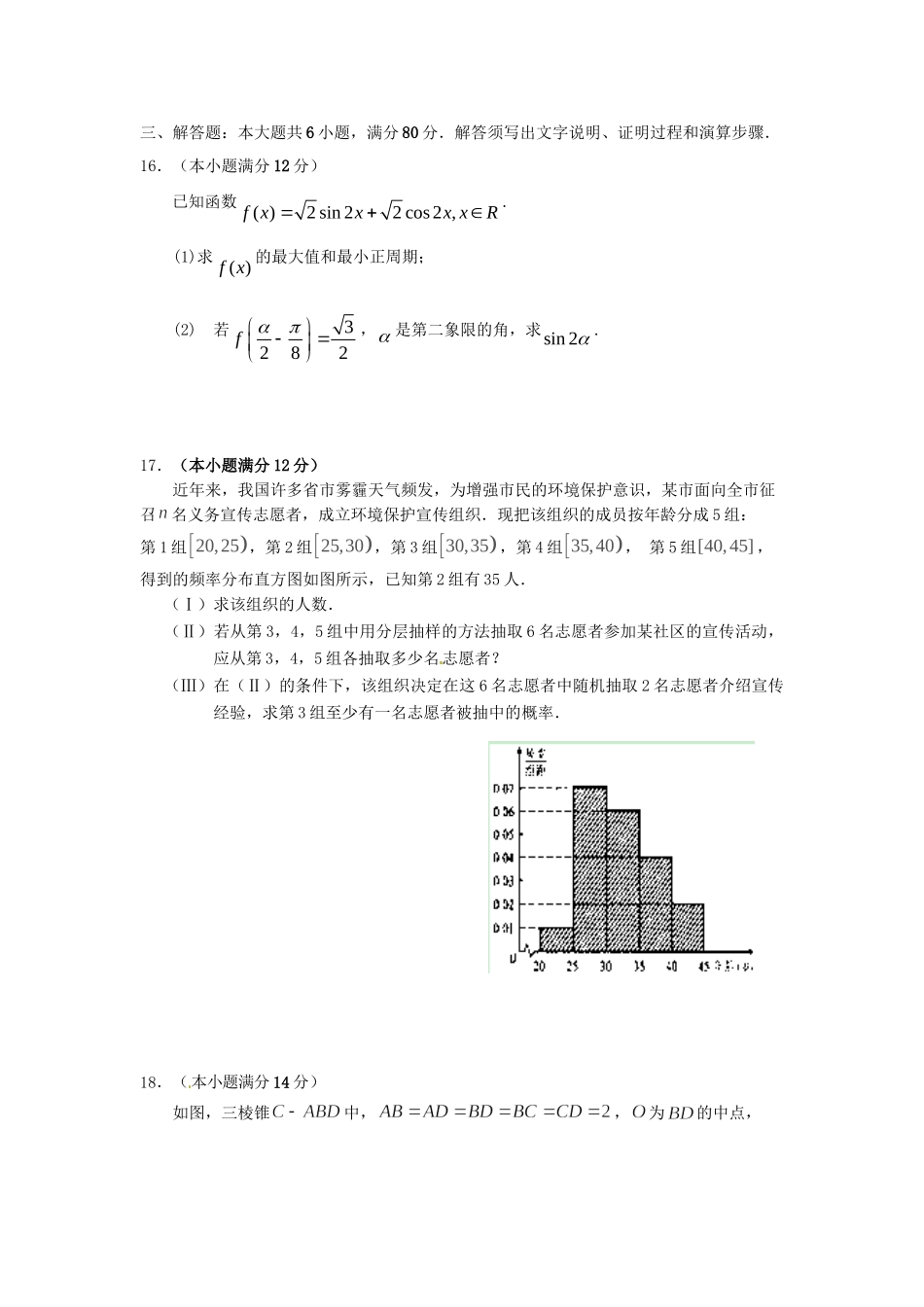
—学年度高三级三模联考试卷文科数学一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知i为虚数单位，则复数A．B．C．D．2．已知集合,，则A．B．C．D．3.已知(1,),(,4)akbk“，那么2k”“是,ab”共线的A．充分非必要条件B．必要非充分条件C．非充分非必要条件D．充要条件4．先后抛掷两颗质地均匀的骰子，则两次朝上的点数之积为奇数的概率为A．B．C．D．5.在ABC△中，若CBA222sinsinsin，则ABC△的形状是A.锐角三角形B.钝角三角形C.直角三角形D.不能确定6．某几何体的三视图如图所示，则该几何体的体积为A.48B.C.16D.327．已知偶函数f（x），当时，f（x）=2sinx，当时，，则A．B．1C．3D．8.曲线221259xy与曲线221(9)259xykkk的A.长轴长相等B.短轴长相等C.离心率相等D.焦距相等9.指数函数与二次函数在同一坐标系中的图象可能的是10．对于集合A“，如果定义了一种运算”，使得集合A中的元素间满足下列4个条件：（ⅰ）,abA，都有abA；（ⅱ）eA，使得对aA，都有eaaea；（ⅲ）aA，aA，使得aaaae；（ⅳ）,,abcA，都有abcabc，则称集合A“对于运算”“”构成对称集．“下面给出三个集合及相应的运算”：①A整数“，运算”为普通加法；②A复数“，运算”为普通减法；③A正实数“，运算”为普通乘法．“”其中可以构成对称集的有A.①②B.①③C.②③D.①②③二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分．（一）必做题（11～13题）11．已知函数，则在点处的切线方程为.12．设,其中实数满足,若的最大值为12,则实数________.13、在各项均为正项的等比数列，已知，则（二）选做题（14～15题，考生只能从中选做一题）14．（几何证明选讲选做题）在梯形中，∥，，，点、分别在、上，且∥，若，则的长为．15．（坐标系与参数方程选做题）在平面直角坐标系中，已知直线l与曲线C的参数方程分别为l：1,1xsys（s为参数）和C：22,xtyt（t为参数），若l与C相交于A、B两点，则AB．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（本小题满分12分）已知函数()2sin22cos2,fxxxxR.(1)求()fx的最大值和最小正周期；(2)若3282f，是第二象限的角，求sin2.17．（本小题满分12分）近年来，我国许多省市雾霾天气频发，为增强市民的环境保护意识，某市面向全市征召名义务宣传志愿者，成立环境保护宣传组织．现把该组织的成员按年龄分成5组：第1组20,25，第2组25,30，第3组30,35，第4组35,40，第5组[40,45]，得到的频率分布直方图如图所示，已知第2组有35人．（Ⅰ）求该组织的人数．（Ⅱ）若从第3，4，5组中用分层抽样的方法抽取6名志愿者参加某社区的宣传活动，应从第3，4，5组各抽取多少名志愿者？（Ⅲ）在（Ⅱ）的条件下，该组织决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验，求第3组至少有一名志愿者被抽中的概率．18．（本小题满分14分）如图，三棱锥中，，为的中点，，为上一点，为上一点，且．（Ⅰ）求证：∥平面；（Ⅱ）求证：⊥平面；（Ⅲ）求四面体ABCD的体积。19．（本小题满分14分）已知是等差数列，公差为，首项，前项和为.令,的前项和.数列满足，.（Ⅰ）求数列的通项公式；（Ⅱ）若，，求的取值范围.20.（本小题满分14分）已知椭圆2222:10xyCabab的右焦点1F与抛物线24yx的焦点重合，原点到过点,0,0,AaBb的直线的距离是2217.（Ⅰ）求椭圆C的方程；（Ⅱ）设动直线:lykxm与椭圆C有且只有一个公共点，过1F作1PF的垂线与直线l交于点，求证：点在定直线上，并求出定直线的方程.21、（本小题满分14分）已知函数（1）求函数的单调区间；（2）当时，求函数在上的最大值。三模参考答案及评分标准CBACBDADCB11.12.213.414.15.216.解：(1) 22()2sin2cos22cossin2sincos22244fxxxxx...