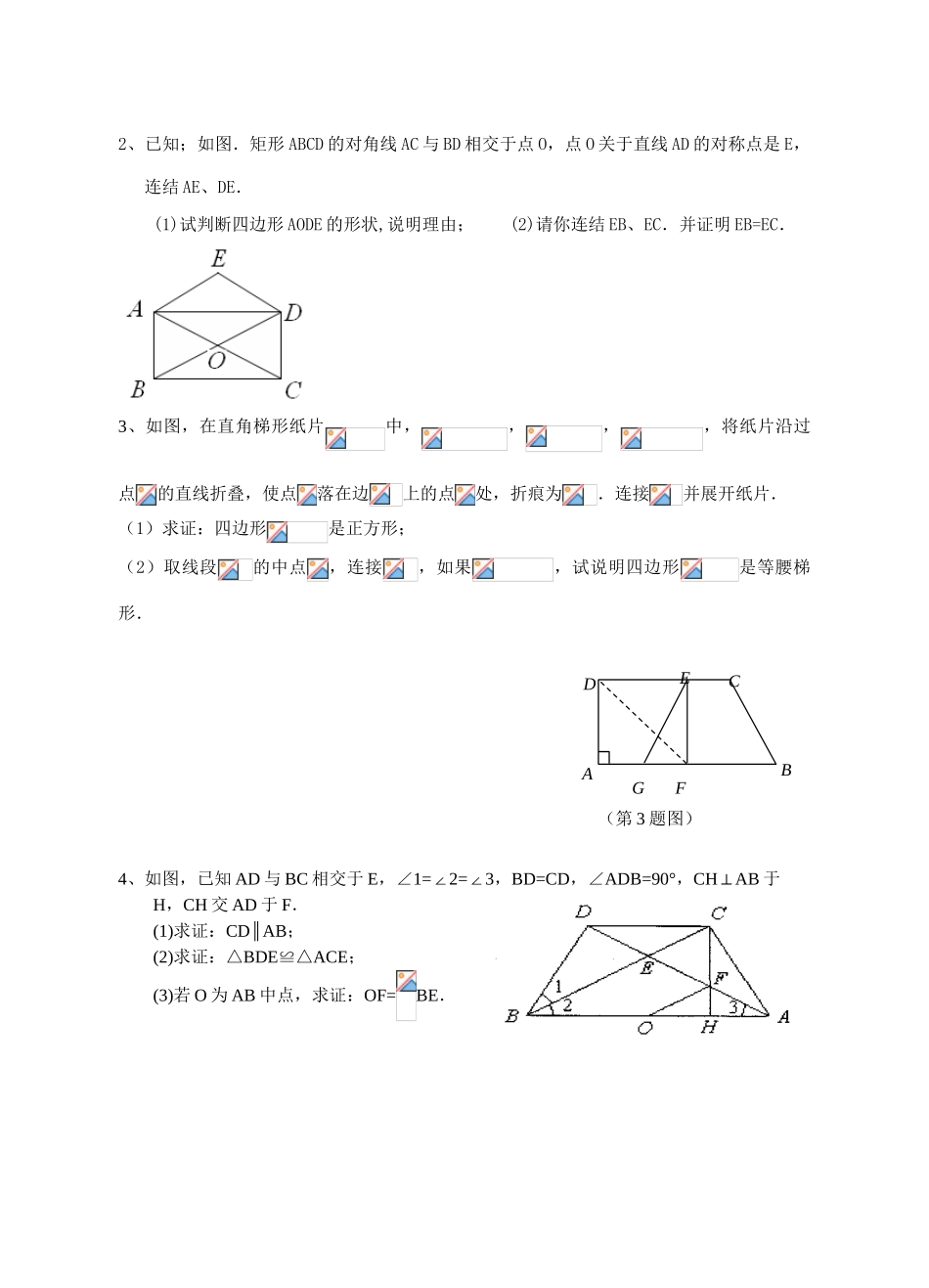
第一章小结与思考教学案学习目标:通过对本章知识的小结与梳理,进一步掌握等腰三角形的性质和判定、直角三角形全等的判定、角平分线的性质定理与判定定理、特殊四边形(平行四边形、矩形、菱形、正方形)的定义、性质和判定;等腰梯形的性质和判定;中位线定理,并会灵活运用.学习重点:性质定理和判定定理的应用学习难点:性质定理和判定定理的应用学习过程:一、基础练习1、等腰三角形的一个底角为,则顶角的度数是度.2、等腰三角形的两边长分别为4和9,则第三边长为.3、下列命题为真命题的是()A:三角形的中位线把三角形的面积分成相等的两部分;B:对角线相等且相互平分的四边形是正方形;C:关于某直线对称的两个三角形是全等三角形;D:一组对边平行,另一组对边相等的四边形一定是等腰梯形4、下列命题是假命题的是()A:四个角相等的四边形是矩形;B:对角线互相平分的四边形是平行四边形;C:四条边相等的四边形是菱形;D:对角线互相垂直且相等的四边形是正方形5、如图在中,∠ABC的平分线交AD于E,且AE=2,DE=1,则的周长等于.6、如图,点D、E、F分别是三边上的中点.若的面积为12,则的面积为.二、例题学习1、如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.(1)求证:AD⊥CF;(2)连接AF,试判断△ACF的形状,并说明理由.(第5题)ABCFED2、已知;如图.矩形ABCD的对角线AC与BD相交于点O,点O关于直线AD的对称点是E,连结AE、DE.(1)试判断四边形AODE的形状,说明理由;(2)请你连结EB、EC.并证明EB=EC.3、如图,在直角梯形纸片中,,,,将纸片沿过点的直线折叠,使点落在边上的点处,折痕为.连接并展开纸片.(1)求证:四边形是正方形;(2)取线段的中点,连接,如果,试说明四边形是等腰梯形.4、如图,已知AD与BC相交于E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于H,CH交AD于F.(1)求证:CD∥AB;(2)求证:△BDEACE≌△;(3)若O为AB中点,求证:OF=BE.ECBDAGF(第3题图)三、作业:见作业纸。08-09学年度第一学期九年级数学作业纸内容:第一章小结与思考(1)班级姓名日期月日等第1、(1)已知等腰三角形的腰长是6cm,底边长是8cm,那么以各边中点为顶点的三角形的周长是___________cm.(2)顺次连接等腰梯形的四边中点所得的四边形是。2、梯形的中位线长为3,高为2,则该梯形的面积为3、如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由点开始按的顺序沿菱形的边循环运动,行走2008厘米后停下,则这只蚂蚁停在点.4、如图,小亮用六块形状、大小完全相同的等腰梯形拼成一个四边形,则图中的度数是()A.B.C.D.5、如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有()A.1个B.2个C.3个D.4个6、如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为()A.5:3B.3:5C.4:3D.3:47、如图,已知平行四边形中,对角线交于(第2题图)CAFDEBG(第3题图)点,是延长线上的点,且是等边三角形.(1)求证:四边形是菱形;(2)若,求证:四边形是正方形.8、如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.(2)将原题中正方形改为矩形(如图4—6),且AB=a,BC=b,CE=ka,CG=kb(ab,k0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.ECDBAO(3)在第(2)题图5中,连结、,且a=3,b=2,k=,求的值.