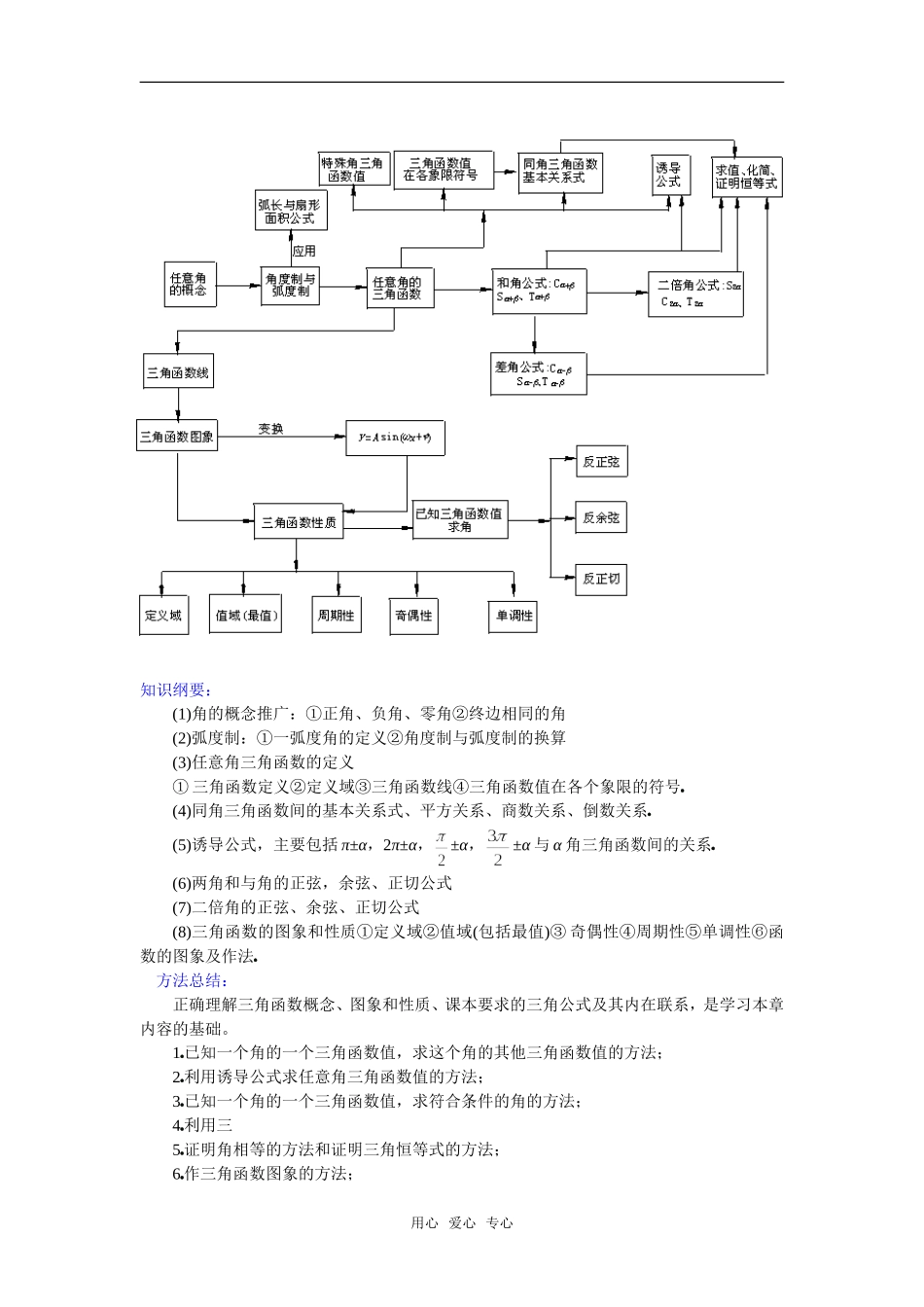
课题:小结与复习(1)知识目标:1奎屯王新敞新疆任意角的三角函数、任意角的概念、弧度制、任意角的三角函数的概念、同角三角函数间的关系、诱导公式;2奎屯王新敞新疆两角和与差的三角函数、二倍角的三角函数;3奎屯王新敞新疆三角函数的图象和性质、已知三角函数值求角奎屯王新敞新疆教学目的:1奎屯王新敞新疆理解任意角的概念、弧度的意义;能正确地进行弧度与角度的换算;2奎屯王新敞新疆掌握任意角的正弦、余弦、正切的定义,并会利用与单位圆有关的三角函数线表示正弦、余弦和正切;了解任意角的余切、正割、余割的定义;掌握同角三角函数的基本关系式;掌握正弦、余弦的诱导公式;3奎屯王新敞新疆掌握两角和与两角差的正弦、余弦、正切公式;掌握二倍角的正弦、余弦、正切公式;4奎屯王新敞新疆能正确运用三角公式,进行三角函数式的化简、求值及恒等式证明;5奎屯王新敞新疆会用与单位圆有关的三角函数线画出正弦函数、正切函数的图象,并在此基础上由诱导公式画出余弦函数的图象;理解周期函数与最小正周期的意义;并通过它们的图象理解正弦函数、余弦函数、正切函数的性质;会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+)的简图,理解A、ω、的物理意义;6奎屯王新敞新疆会用已知三角函数值求角,并会用符号arcsinx、arccosx、arctanx表示奎屯王新敞新疆教学重点:三角函数的知识网络结构及各部分知识奎屯王新敞新疆教学难点:熟练掌握各部分知识,并能灵活应用其解决相关问题德育目标:1奎屯王新敞新疆渗透“变换”思想、“化归”思想;2奎屯王新敞新疆培养逻辑推理能力;3奎屯王新敞新疆培养学生探求精神奎屯王新敞新疆教学方法:引导式运用“整体化”教学思想,引导学生生从“整体”到“局部”再到“整体”逐步认识奎屯王新敞新疆授课类型:复习课课时安排:1课时教具:多媒体、实物投影仪教学过程:一、本章知识与方法总结:知识结构用心爱心专心知识纲要:(1)角的概念推广:①正角、负角、零角②终边相同的角(2)弧度制:①一弧度角的定义②角度制与弧度制的换算(3)任意角三角函数的定义①三角函数定义②定义域③三角函数线④三角函数值在各个象限的符号奎屯王新敞新疆(4)同角三角函数间的基本关系式、平方关系、商数关系、倒数关系奎屯王新敞新疆(5)诱导公式,主要包括π±α,2π±α,±α,±α与α角三角函数间的关系奎屯王新敞新疆(6)两角和与角的正弦,余弦、正切公式(7)二倍角的正弦、余弦、正切公式(8)三角函数的图象和性质①定义域②值域(包括最值)③奇偶性④周期性⑤单调性⑥函数的图象及作法奎屯王新敞新疆方法总结:正确理解三角函数概念、图象和性质、课本要求的三角公式及其内在联系,是学习本章内容的基础。1奎屯王新敞新疆已知一个角的一个三角函数值,求这个角的其他三角函数值的方法;2奎屯王新敞新疆利用诱导公式求任意角三角函数值的方法;3奎屯王新敞新疆已知一个角的一个三角函数值,求符合条件的角的方法;4奎屯王新敞新疆利用三5奎屯王新敞新疆证明角相等的方法和证明三角恒等式的方法;6奎屯王新敞新疆作三角函数图象的方法;用心爱心专心7奎屯王新敞新疆三角函数图象变换的方法;8奎屯王新敞新疆研究三角函数性质的方法奎屯王新敞新疆二、讲解新课:这一章的知识网络结构:最先,我们给出了三角函数的定义,包括任意角的三角函数的符号,同角三角函数的关系式,诱导公式,两角和与差的三角函数公式,以及它们的变形公式等等奎屯王新敞新疆然后,我们又共同学习了三角函数(主要是:正弦函数、余弦函数、正切函数)的图象和性质奎屯王新敞新疆接下来,我们又共同探讨了它们的应用奎屯王新敞新疆运用上述公式和性质主要是进行三角函数式的化简、求值、证明以及它们的综合运用奎屯王新敞新疆具体内容:根据生产实际和进一步学习数学的需要,我们引入了任意角的概念,并学习了角的另一种单位制——弧度制奎屯王新敞新疆这里规定长度等于半径长的弧所对的圆心角叫做1弧度的角奎屯王新敞新疆于是,弧长公式为:l=|α|r(其中l′为弧长,r为半径,α为圆弧所对圆心角的弧度数)之后,我们定义了任意角的正弦、余弦、正切、余切、正...