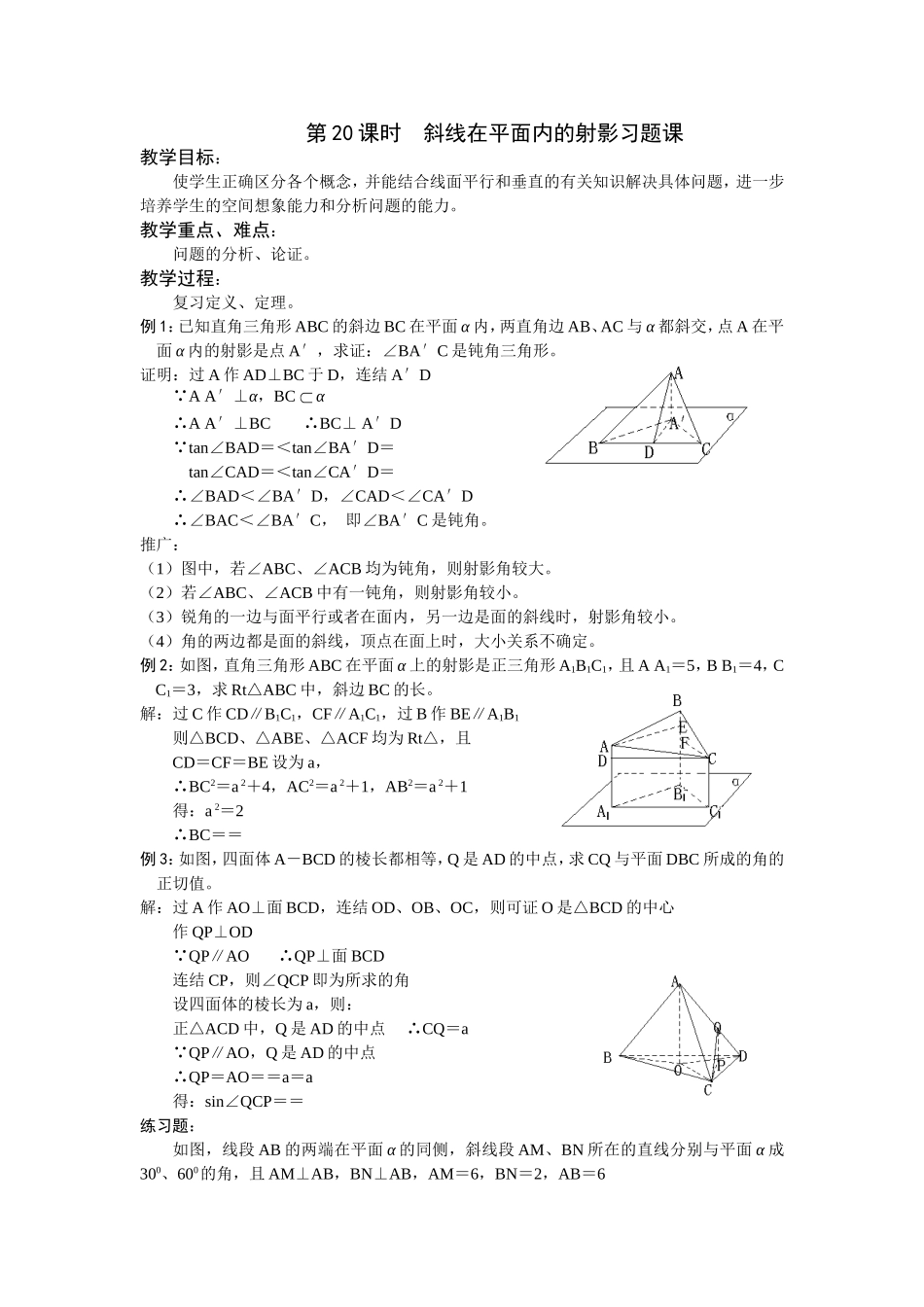
第20课时斜线在平面内的射影习题课教学目标:使学生正确区分各个概念,并能结合线面平行和垂直的有关知识解决具体问题,进一步培养学生的空间想象能力和分析问题的能力。教学重点、难点:问题的分析、论证。教学过程:复习定义、定理。例1:已知直角三角形ABC的斜边BC在平面α内,两直角边AB、AC与α都斜交,点A在平面α内的射影是点A′,求证:∠BA′C是钝角三角形。证明:过A作AD⊥BC于D,连结A′D∵AA′⊥α,BCα∴AA′⊥BC∴BC⊥A′D∵tan∠BAD=<tan∠BA′D=tan∠CAD=<tan∠CA′D=∴∠BAD<∠BA′D,∠CAD<∠CA′D∴∠BAC<∠BA′C,即∠BA′C是钝角。推广:(1)图中,若∠ABC、∠ACB均为钝角,则射影角较大。(2)若∠ABC、∠ACB中有一钝角,则射影角较小。(3)锐角的一边与面平行或者在面内,另一边是面的斜线时,射影角较小。(4)角的两边都是面的斜线,顶点在面上时,大小关系不确定。例2:如图,直角三角形ABC在平面α上的射影是正三角形A1B1C1,且AA1=5,BB1=4,CC1=3,求Rt△ABC中,斜边BC的长。解:过C作CD∥B1C1,CF∥A1C1,过B作BE∥A1B1则△BCD、△ABE、△ACF均为Rt△,且CD=CF=BE设为a,∴BC2=a2+4,AC2=a2+1,AB2=a2+1得:a2=2∴BC==例3:如图,四面体A-BCD的棱长都相等,Q是AD的中点,求CQ与平面DBC所成的角的正切值。解:过A作AO⊥面BCD,连结OD、OB、OC,则可证O是△BCD的中心作QP⊥OD∵QP∥AO∴QP⊥面BCD连结CP,则∠QCP即为所求的角设四面体的棱长为a,则:正△ACD中,Q是AD的中点∴CQ=a∵QP∥AO,Q是AD的中点∴QP=AO==a=a得:sin∠QCP==练习题:如图,线段AB的两端在平面α的同侧,斜线段AM、BN所在的直线分别与平面α成300、600的角,且AM⊥AB,BN⊥AB,AM=6,BN=2,AB=6(1)求证:AB∥α;(2)求MN的长。(1)证明:作A、B在平面α上的射影A′、B′连结MA′、NB′、A′B′。(1)(2)在Rt△AMA′中,AM=6,∠AMA′=300,AA′⊥A′M∴AA′=AM=3,同理:BB′=BN=3∴AA′=BB′且AA′∥BB′∴四边形AA′B′B为平行四边形∵AB∥A′B′,且ABα∴AB∥α(2)解:∵AM⊥AB,AB∥A′B′∴A′B′⊥AM又:A′B′⊥AA′,AM∩AA′=A∴A′B′⊥面AMA′∴A′B′⊥A′M同理:A′B′⊥B′N∴MA′∥NB′又:MA′=AM·cos300=3NB′=BN·cos600=由(1)知,A′B′=AB=6如图(1),则MN==4如图(2),则MN==2课堂小结:注意空间想象和空间问题转化为平面问题的方法,并紧密联系有关的定义、定理等。课后作业: