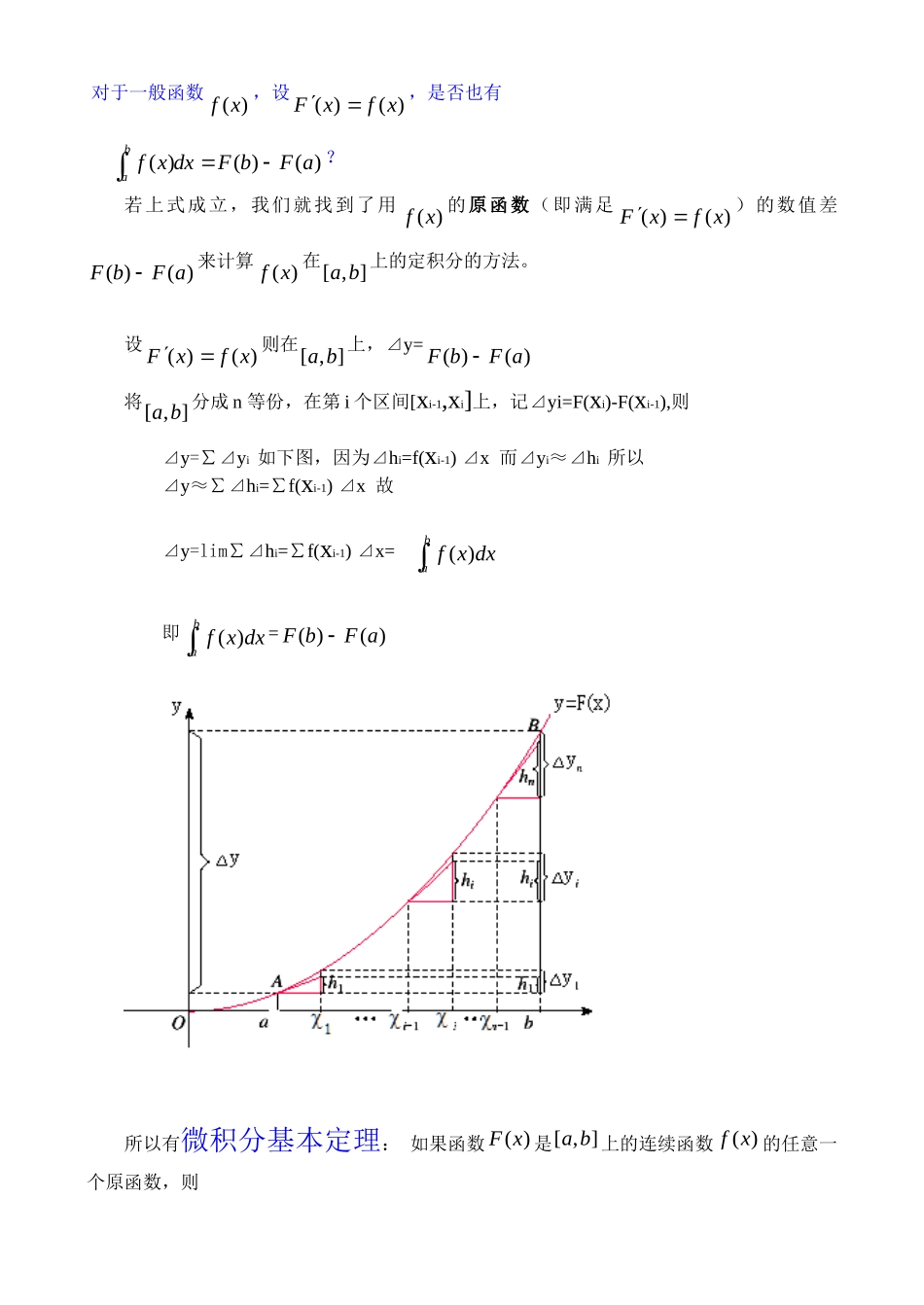
1.6微积分基本定理一:教学目标知识与技能目标通过实例,直观了解微积分基本定理的内容,会用牛顿-莱布尼兹公式求简单的定积分过程与方法通过实例探求微分与定积分间的关系,体会微积分基本定理的重要意义情感态度与价值观通过微积分基本定理的学习,体会事物间的相互转化、对立统一的辩证关系,培养学生辩证唯物主义观点,提高理性思维能力。二:教学重难点重点:通过探究变速直线运动物体的速度与位移的关系,使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分。难点:了解微积分基本定理的含义三:教学过程:1、知识链接:定积分的概念:用定义计算的步骤:2、合作探究:⑴导数与积分的关系;我们讲过用定积分定义计算定积分,但其计算过程比较复杂,所以不是求定积分的一般方法。有没有计算定积分的更直接方法,也是比较一般的方法呢?下面以变速直线运动中位置函数与速度函数之间的联系为例:设一物体沿直线作变速运动,在时刻t时物体所在位置为S(t),速度为v(t)(()vto),则物体在时间间隔12[,]TT内经过的路程可用速度函数表示为21()TTvtdt。另一方面,这段路程还可以通过位置函数S(t)在12[,]TT上的增量12()()STST来表达,即21()TTvtdt=12()()STST而()()Stvt。说出你的发现⑵微积分基本定理对于一般函数()fx,设()()Fxfx,是否也有()()()bafxdxFbFa?若上式成立,我们就找到了用()fx的原函数(即满足()()Fxfx)的数值差()()FbFa来计算()fx在[,]ab上的定积分的方法。设()()Fxfx则在[,]ab上,⊿y=()()FbFa将[,]ab分成n等份,在第i个区间[xi-1,xi]上,记⊿yi=F(xi)-F(xi-1),则⊿y=∑⊿yi如下图,因为⊿hi=f(xi-1)⊿x而⊿yi≈⊿hi所以⊿y≈∑⊿hi=∑f(xi-1)⊿x故⊿y=lim∑⊿hi=∑f(xi-1)⊿x=badxxf)(即badxxf)(=()()FbFa所以有微积分基本定理:如果函数()Fx是[,]ab上的连续函数()fx的任意一个原函数,则()()()bafxdxFbFabadxxf)((此处并不要求学生理解证明的过程)为了方便起见,还常用()|baFx表示()()FbFa,即()()|()()bbaafxdxFxFbFa该式称之为微积分基本公式或牛顿—莱布尼兹公式。它指出了求连续函数定积分的一般方法,把求定积分的问题,转化成求原函数的问题,是微分学与积分学之间联系的桥梁。它不仅揭示了导数和定积分之间的内在联系,同时也提供计算定积分的一种有效方法,为后面的学习奠定了基础。因此它在教材中处于极其重要的地位,起到了承上启下的作用,不仅如此,它甚至给微积分学的发展带来了深远的影响,是微积分学中最重要最辉煌的成果。⑶应用举例例1.计算下列定积分:(1)211dxx;(2)3211(2)xdxx。解:(1)因为'1(ln)xx,所以22111ln|ln2ln1ln2dxxx。(2))因为2''211()2,()xxxx,所以3332211111(2)2xdxxdxdxxx233111122||(91)(1)33xx。练习:计算120xdx解:由于313x是2x的一个原函数,所以根据牛顿—莱布尼兹公式有120xdx=3101|3x=33111033=13例2.计算下列定积分:2200sin,sin,sinxdxxdxxdx。由计算结果你能发现什么结论?试利用曲边梯形的面积表示所发现的结论。解:因为'(cos)sinxx,所以00sin(cos)|(cos)(cos0)2xdxx,22sin(cos)|(cos2)(cos)2xdxx,2200sin(cos)|(cos2)(cos0)0xdxx.可以发现,定积分的值可能取正值也可能取负值,还可能是0:(l)当对应的曲边梯形位于x轴上方时(图1.6一3),定积分的值取正值,且等于曲边梯形的面积;图1.6一3(2)(2)当对应的曲边梯形位于x轴下方时(图1.6一4),定积分的值取负值,且等于曲边梯形的面积的相反数;(3)当位于x轴上方的曲边梯形面积等于位于x轴下方的曲边梯形面积时,定积分的值为0(图1.6一5),且等于位于x轴上方的曲边梯形面积减去位于x轴下方的曲边梯形面积.例3.汽车以每小时32公里速度行驶,到某处需要减速停车。设汽车以等减速度a=1.8米/秒2刹车,问从开始刹车到停车,汽车走了多少距离?解:首先要求出从刹车开始到停车经过了多少时...