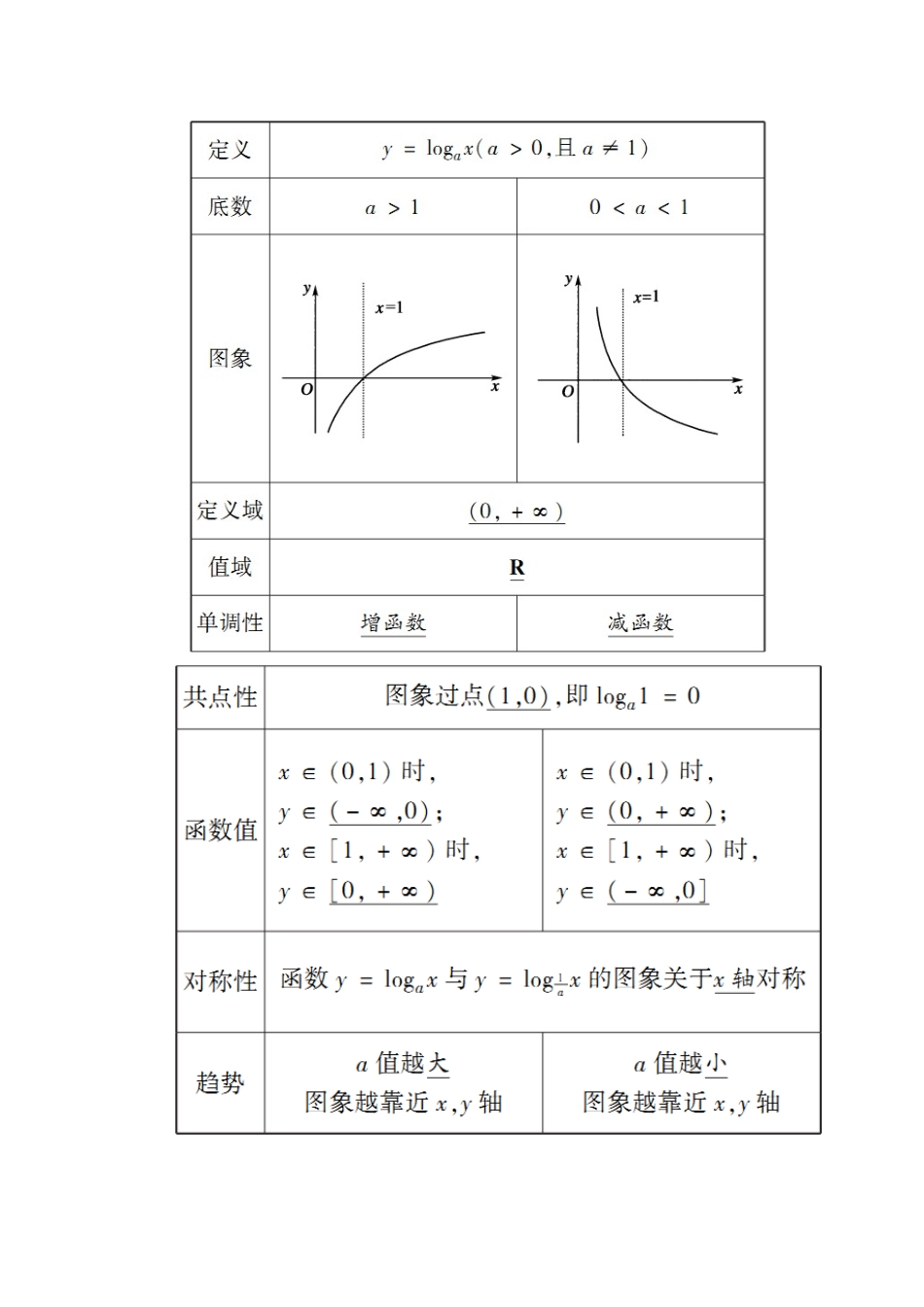
第1课时对数函数的图象与性质[目标]1.记住对数函数的定义、图象和性质;2.会利用对数函数的图象和性质解答有关问题;培养直观想象核心素养.[重点]对数函数的定义、图象和性质.[难点]对数函数性质的概括总结.知识点一对数函数的概念[填一填]1.一般地,我们把函数y=logax(a>0,且a≠1)叫做对数函数,其中x是自变量.2.对数函数y=logax的定义域为(0,+∞),值域为R.[答一答]1.为什么在对数函数中要求a>0,且a≠1?提示:根据对数式与指数式的关系知,y=logax可化为ay=x,联想指数函数中底数的范围,可知a>0,且a≠1.2.下列函数是对数函数的是(C)A.y=loga2x(a>0,a≠1)B.y=loga(x2+1)(a>0,a≠1)C.y=log\f(1,ax(a>0,a≠1)D.y=2lgx解析:在对数函数的定义表达式y=logax(a>0且a≠1)中,logax前面的系数必须是1,自变量x在真数的位置上,否则不是对数函数.所以选C.知识点二对数函数的图象与性质[填一填][答一答]3.怎样可以快速画出对数函数y=logax(a>0,且a≠1)的草图?提示:根据对数函数的性质可知,对数函数的图象都经过点(,-1),(1,0),(a,1),且图象都在第一、四象限内,据此可以快速地画出对数函数y=logax的草图.4.对数函数y=logax(a>0且a≠1),当a>1,x取何值时,y>0?x取何值时,y<0?当0
1时,若x>1,则y>0;若01,则y<0;若00.类型一对数函数的概念[例1]已知对数函数f(x)的图象过点.①求f(x)的解析式;②解方程f(x)=2.[分析]根据已知设出函数解析式,代入点的坐标求出对数函数的底数;然后利用“指对互化”解方程.[解]①由题意设f(x)=logax(a>0,且a≠1),由函数图象过点可得f(4)=,即loga4=,所以4=a,解得a=16,故f(x)=log16x.②方程f(x)=2,即log16x=2,所以x=162=256.利用待定系数法求对数函数的解析式时,常常遇到解方程,比如logam=n,这时先把对数式logam=n化为指数式的形式an=m,把m化为以n为指数的指数幂形式m=knk>0,且k≠1,解得a=k>0.还可以直接写出a=m,再利用指数幂的运算性质化简m.[变式训练1](1)已知对数函数f(x)的图象过点(8,3),则f=-5.(2)已知函数f(x)=(2m2-m)logax+m-1是对数函数,则m=1.解析:(1)设f(x)=logax(a>0,且a≠1),则3=loga8,∴a3=8,a=2.∴f(x)=log2x,f=log2=log22-5=-5.(2)因为函数f(x)是对数函数,则解得m=1.类型二对数函数图象的有关问题命题视角1:对数函数的底与图象变化的关系[例2]对数函数y=logax,y=logbx,y=logcx,y=logdx在同一坐标系内的图象如图所示,则a,b,c,d的大小关系是________.[答案]a>b>c>d[解析]利用数形结合法,画出直线y=1判断,亦可根据在第一象限内顺时针旋转底数逐渐增大解决.如图,作直线y=1,则该直线与各函数图象必各交于一点,由logaa=1可知,各交点的横坐标分别为各函数底数,从而可知a>b>c>d.在第一象限内顺时针旋转,底数逐渐增大,故a>b>c>d.当01时,对数函数的图象是上升的,而且随着a由小变大,图象上升的速度变慢.[变式训练2]已知a>0,且a≠1,则函数y=ax与y=loga(-x)的图象只能是(B)解析:方法一若01,则函数y=ax的图象上升且过点(0,1),而函数y=loga(-x)的图象下降且过点(-1,0),只有B中图象符合.方法二首先指数函数y=ax的图象只可能在上半平面,函数y=loga(-x)的图象只可能在左半平面,从而排除A,C;再看单调性,y=ax与y=loga(-x)的单调性正好相反,排除D.只有B中图象符合.命题视角2:图象过定点问题[例3]函数y=loga(x+1)-2(a>0,且a≠1)的图象恒过点________.[答案](0,-2)[解析]因为函数y=logax(a>0,且a≠1)的图象恒过点(1,0),则令x+1=1得x=0,此时y=loga(x+1)-2=-2,所以函数y=loga(x+1)-2(a>0,且a≠1)的图象恒过点(0,-2).求函数y=m+logafxa>0,且a≠1的图象过的定点时,只需...