高中数学 1.3.1《正弦函数的图像与性质》教案1 新人教B版必修4VIP免费

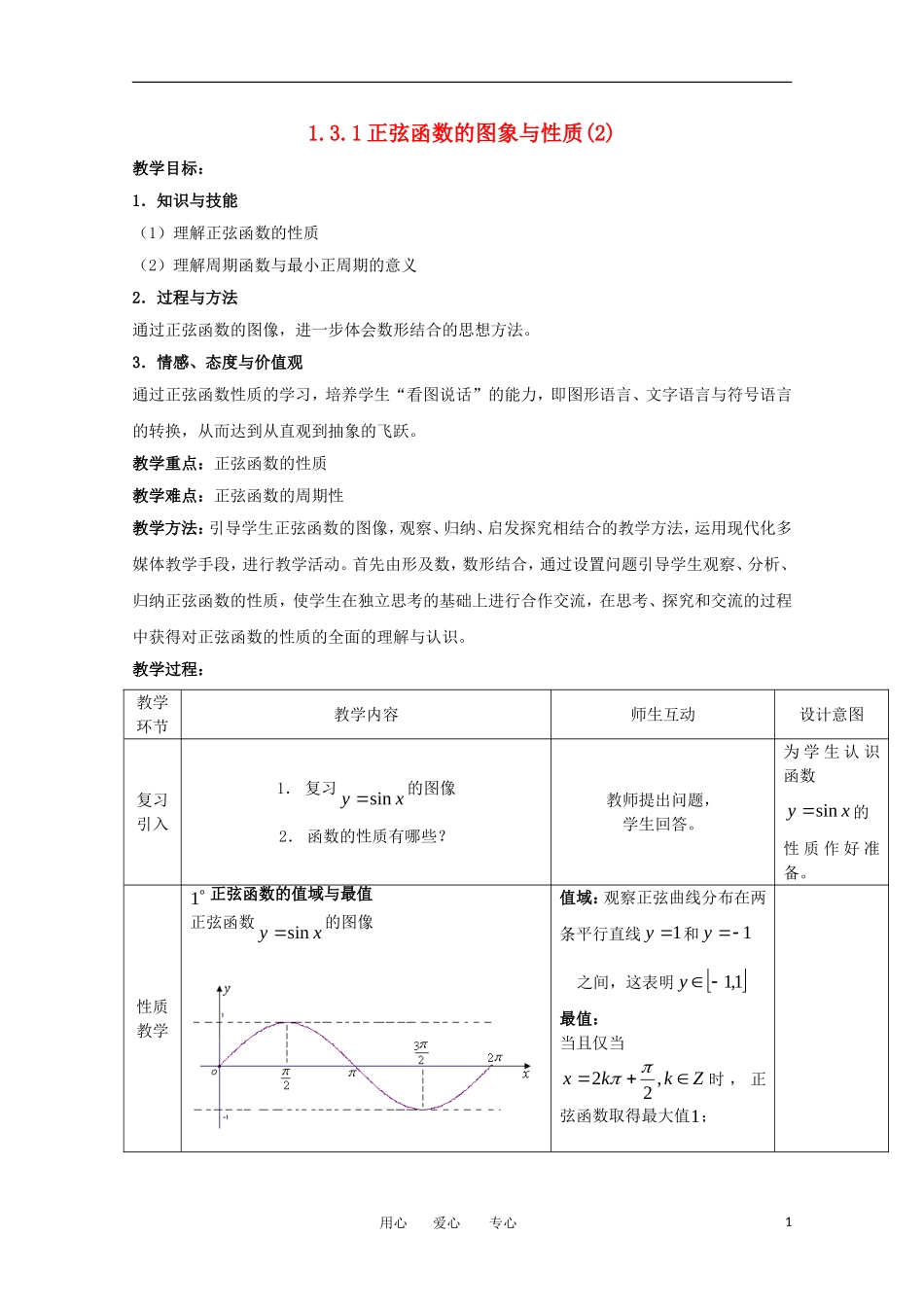
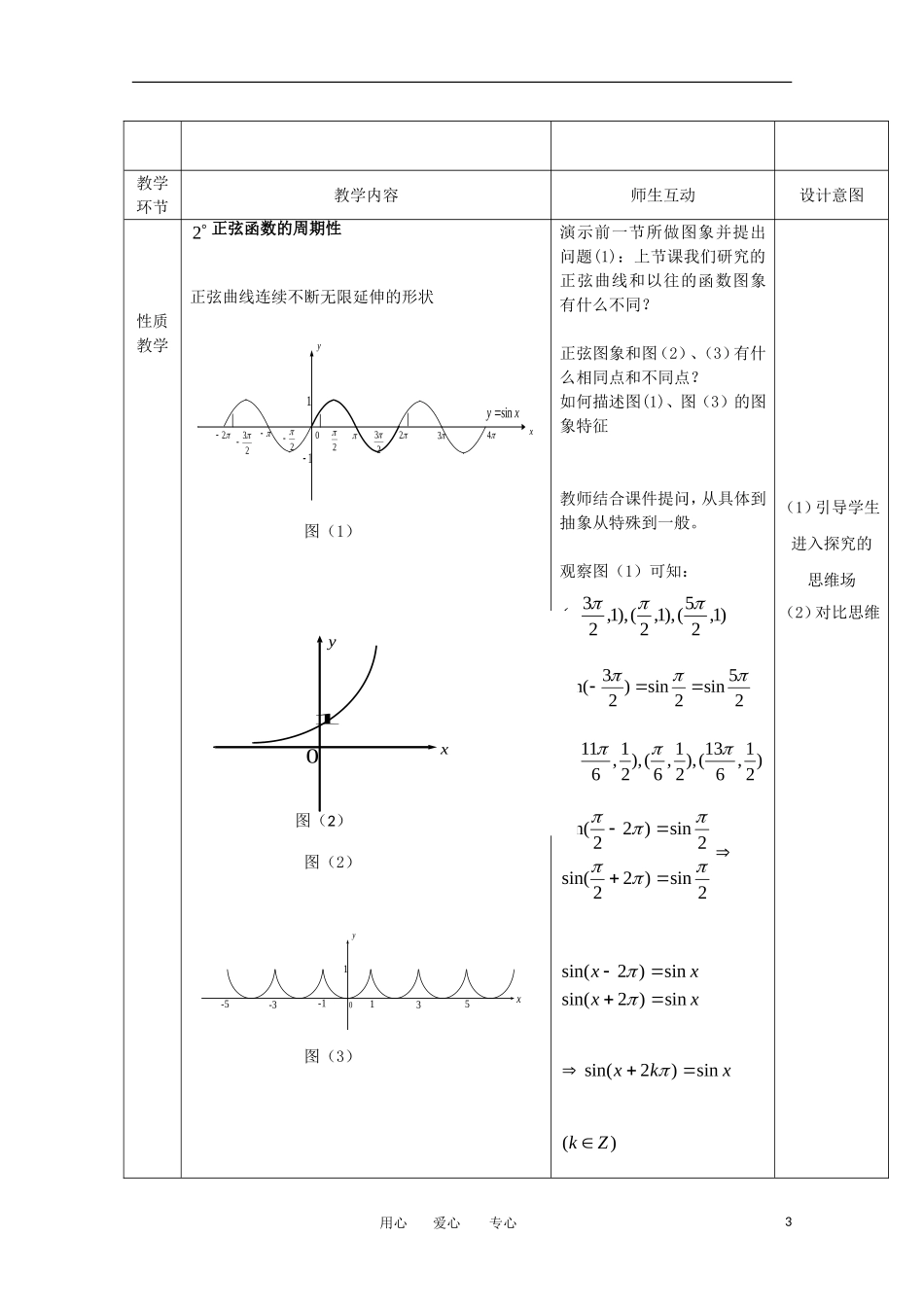
1.3.1正弦函数的图象与性质(2)教学目标：1．知识与技能（1）理解正弦函数的性质（2）理解周期函数与最小正周期的意义2．过程与方法通过正弦函数的图像，进一步体会数形结合的思想方法。3．情感、态度与价值观通过正弦函数性质的学习，培养学生“看图说话”的能力，即图形语言、文字语言与符号语言的转换，从而达到从直观到抽象的飞跃。教学重点：正弦函数的性质教学难点：正弦函数的周期性教学方法：引导学生正弦函数的图像，观察、归纳、启发探究相结合的教学方法，运用现代化多媒体教学手段，进行教学活动。首先由形及数，数形结合，通过设置问题引导学生观察、分析、归纳正弦函数的性质，使学生在独立思考的基础上进行合作交流，在思考、探究和交流的过程中获得对正弦函数的性质的全面的理解与认识。教学过程：教学环节教学内容师生互动设计意图复习引入1．复习xysin的图像2．函数的性质有哪些？教师提出问题，学生回答。为学生认识函数xysin的性质作好准备。性质教学1正弦函数的值域与最值正弦函数xysin的图像值域：观察正弦曲线分布在两条平行直线1y和1y之间，这表明1,1y最值：当且仅当Zkkx,22时，正弦函数取得最大值1；用心爱心专心1教学环节教学内容师生互动设计意图性质教学动态演示正弦线的运动：当且仅当Zkkx,22时，正弦函数取得最大值1；观察正弦线的变化得：值域：正弦线的长度小于或等于单位圆半径的长度，这表明1,1y最值：当角的终边与y轴的正半轴重合时，正弦函数取得最大值1，即当且仅当Zkkx,22时，正弦函数取得最大值1；当角的终边与y轴的负半轴重合时，正弦函数取得最小值1，即当且仅当Zkkx,22时，正弦函数取得最小值1；从正弦曲线与正弦线两种途径探索正弦函数的性质，加深对二者的巩固与复习，体会数形结合思想在函数中的作用用心爱心专心2教学环节教学内容师生互动设计意图性质教学2正弦函数的周期性正弦曲线连续不断无限延伸的形状1102232yxxysin342232图（1）图（2）图（3）演示前一节所做图象并提出问题(1)：上节课我们研究的正弦曲线和以往的函数图象有什么不同？正弦图象和图（2）、（3）有什么相同点和不同点？如何描述图(1)、图（3）的图象特征教师结合课件提问，从具体到抽象从特殊到一般。观察图（1）可知：)1,25(),1,2(),1,23(25sin2sin)23sin()21,613(),21,6(),21,611(2sin)22sin(2sin)22sin(xxxxsin)2sin(sin)2sin(xkxsin)2sin()(Zk（1）引导学生进入探究的思维场（2）对比思维用心爱心专心30xy1图（2）y0x1-11-3-535观察图（3）可知：)1,5(),1,3(),1,1(),1,1(),1,3(),1,5()5()3()1()1()3()5(ffffff)()2(xfxf教学环节教学内容师生互动设计意图性质教学定义：对于函数)(xf，如果存在一个非零常数T，使得定义域内的每一个x值，都满足)()(xfTxf，那么函数)(xf就叫做周期函数，非零常数T叫做这个函数的周期.对于一个周期函数)(xf，如果在它的所有周期中存在一个最小的正数，那么这个最小正数就叫做它的最小正周期.说明：正弦函数是一个周期函数，)0,(2kZkk且都是它的周期，2是其最小正周期由图（2）的分析可知：当自变量x的值每增加或减少2的整数倍时，正弦函数的值重复出现.在单位圆中,当角的终边绕原点转动回到原处时,正弦线的数量(长度和符号)不发生变化。师生共同总结函数周期性的定义。从感性认识向理性认识从过渡最后抽象概括并渗透三种语言的转化用心爱心专心4性质教学3正弦函数的奇偶性教师提出问题：1．如何判断函数的奇偶性？2．正弦函数具有奇偶性吗？3．如何判断它的奇偶性？学生回答：1．偶函数xfxf图像关于y轴对称；奇函数xfxf图像关于0,0成中心对称。教学环节教学内容师生互动设计意图性质教学正弦函数xysin的图像4正弦函数的单调性正弦函数xysin的一个周期内的图像中，如图：2．正弦函数具有奇偶性。3．方法一：由诱导公式xxsinsin...