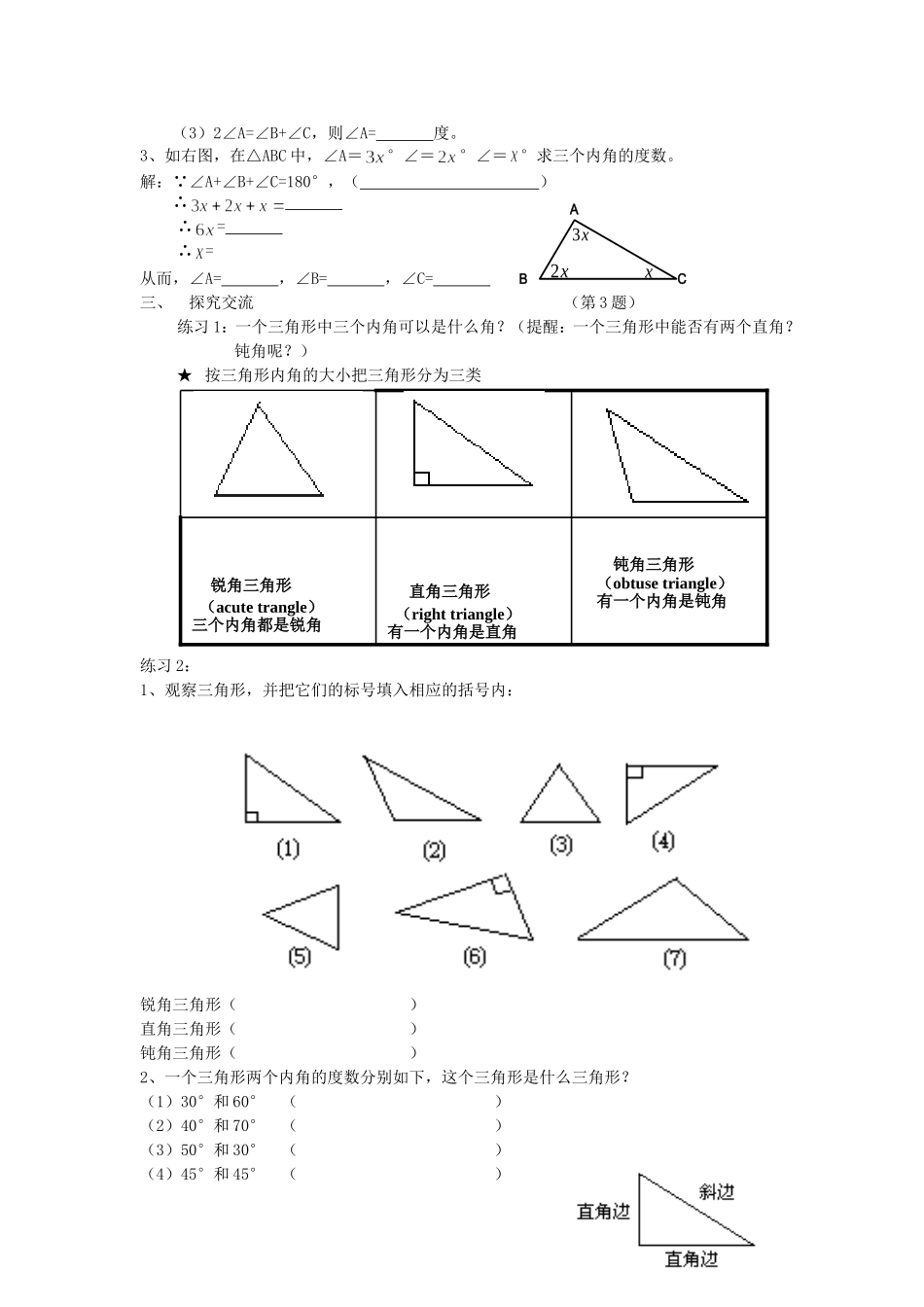
三角形1.认识三角形1、它的三个顶点分别是,三条边分别是,三个内角分别是。2、分别量出这三角形三边的长度,并计算任意两边之和以及任意两边之差。你发现了什么?结论:三角形任意两边之和大于第三边三角形任意两边之差小于第三边例:有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?长度为7cm的木棒呢?二、巩固练习:1、下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗?为什么?(单位:cm)(1)1,3,3(2)3,4,7(3)5,9,13(4)11,12,22(5)14,15,302、已知一个三角形的两边长分别是3cm和4cm,则第三边长X的取值范围是。若X是奇数,则X的值是。这样的三角形有个;若X是偶数,则X的值是,这样的三角形又有个3、一个等腰三角形的一边是2cm,另一边是9cm,则这个三角形的周长是cm夯实基础1、填空:(1)当0°<<90°时,是角;(2)当=°时,是直角;(3)当90°<<180°时,是角;(4)当=°时,是平角。2、如右图, AB∥CE,(已知)∴∠A=,()∴∠B=,()(第2题)二、探索练习:根据知道三角形的三个内角和等于180°,那么是否对其他的三角形也有这样的一个结论呢?(提出问题,激发学生的兴趣)结论:三角形三个内角和等于180°(几何表示)练习1:1、判断:(1)一个三角形的三个内角可以都小于60°;()(2)一个三角形最多只能有一个内角是钝角或直角;()2、在△ABC中,(1)∠C=70°,∠A=50°,则∠B=度;(2)∠B=100°,∠A=∠C,则∠C=度;ABCabcABCDE123(3)2∠A=∠B+∠C,则∠A=度。3、如右图,在△ABC中,∠A=°∠=°∠=°求三个内角的度数。解: ∠A+∠B+∠C=180°,()∴∴=∴=从而,∠A=,∠B=,∠C=三、探究交流(第3题)练习1:一个三角形中三个内角可以是什么角?(提醒:一个三角形中能否有两个直角?钝角呢?)★按三角形内角的大小把三角形分为三类练习2:1、观察三角形,并把它们的标号填入相应的括号内:锐角三角形()直角三角形()钝角三角形()2、一个三角形两个内角的度数分别如下,这个三角形是什么三角形?(1)30°和60°()(2)40°和70°()(3)50°和30°()(4)45°和45°()锐角三角形(acutetrangle)三个内角都是锐角直角三角形(righttriangle)有一个内角是直角钝角三角形(obtusetriangle)有一个内角是钝角x2x3xABC四、猜想结论:简单介绍直角三角形,和表示方法,Rt△思考:直角三角形中的两个锐角有什么关系?结论:直角三角形的两个锐角互余练习3:1、观察下列的直角三角形,分别写出它们符号表示、直角边和斜边。(图1)(图2)(1)图1中的直角三角形用符号写成,直角边是和,斜边是;(2)图2中的直角三角形用符号写成,直角边是和,斜边是;2、如下图,在Rt△CDE,∠C和∠E的关系是,其中∠C=55°,则∠E=度3、如上图,在Rt△ABC中,∠A=2∠B,则∠A=度,∠B=度;2.认识三角形的中线和高1、任意画一个三角形,设法画出它的一个内角的平分线。1、你能通过折纸的方法得到它吗?(可以用量角器来量出这个角的大小的方法画出这个角的平分线。也可以用折纸的方法得到角平分线)。结论:三角形一个角的角平分线和这个角的对边相交,这个角的顶点和对边交点之间的线段叫做三角形中这个角的角平分线。简称三角形的角平分线。A如图: AD是三角形ABC的角平分线。12∴∠1=∠2=∠BAC或:∠BAC=2∠1=2∠2请画出△ABC(锐角三角形)的所有角平分线,并且观察这些角平分线有什么规律?对于钝角三角形呢?直角三角形呢?它们的角平分线也有这样的规律吗?一个三角形共有三条角平分线,它们都在三角形内部,而且相交于一点。连结三角形一个顶点和它对边中点的线段,叫做三角形这个边上的中线。简称三角形的中线。注:规范书面表达,按下面的示范书写:如图: AD是三角形ABC的中线。A∴BD=DC=BC或:BC=2BD=2DCCDEABCBCDEFGBDC结论:一个三角形共有三条中线,它们都在三角形内部,而且相交于一点。如图,已知,AD是BC边上的中线,AB=5cm,AD=4cm,▲ABD的周长是12cm,求BD的长.1、★三角形的高:从三角形的一个顶点向它的对边所在直线...