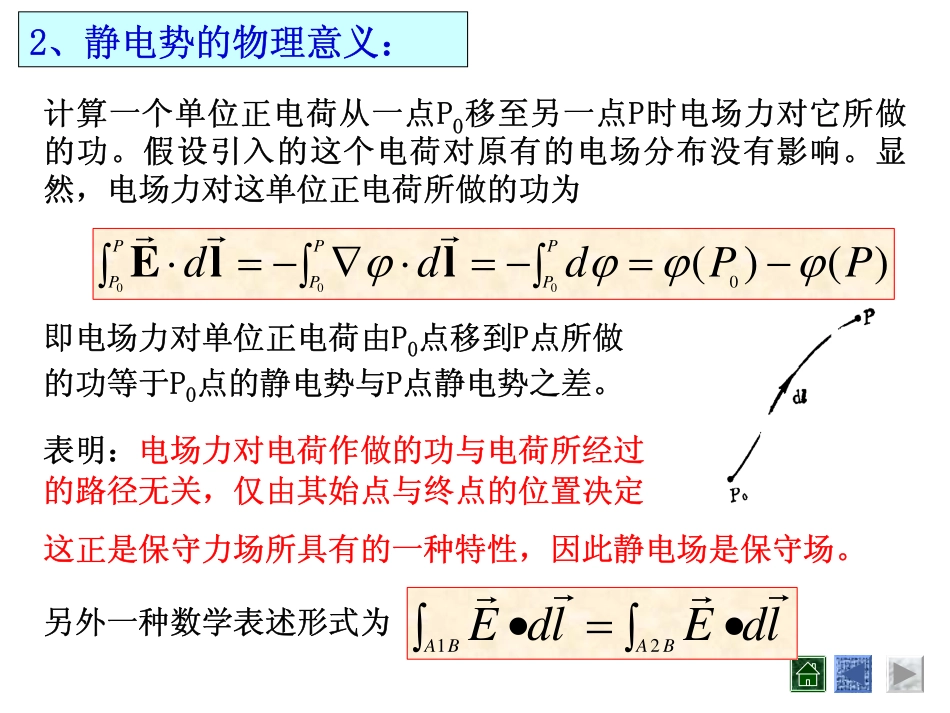
2.1静电场的标势及其微分方程1、标势的引入:ρ=•∇=×∇Drr,0E在电荷静止情况下,电场与磁场无关,麦氏方程组的电场部分表明静电场是无旋场以及自由电荷分布ρ是电位移D的源。这两方程连同介质的电磁性质方程是解决静电问题的基础。一、静电势与电势叠加原理由静电场的无旋性,可以引入一个标势来描述静电场)(rErrϕ−∇=2、静电势的物理意义:图2-1计算一个单位正电荷从一点P0移至另一点P时电场力对它所做的功。假设引入的这个电荷对原有的电场分布没有影响。显然,电场力对这单位正电荷所做的功为)()(0000PPdddPPPPPPϕϕϕϕ−=∫−=∫⋅∇−=∫⋅llErrr即电场力对单位正电荷由P0点移到P点所做的功等于P0点的静电势与P点静电势之差。表明:电场力对电荷作做的功与电荷所经过的路径无关,仅由其始点与终点的位置决定这正是保守力场所具有的一种特性,因此静电场是保守场。另外一种数学表述形式为ldEldEBABArrrr∫•=∫•21需要注意的事项:1、上式只能确定两点的电势差,而不能确定电势的绝对值。只有当场中任意一点的电势值确定之后,场中所有点的电势值才能唯一地确定。3、对于电荷分布在有限空间的情况下,一般都选择无穷远的电势值为零,即,因此0=∞ϕ∫∞⋅=0)(0PdPlEϕ4、用电场强度与静电势描述静电场是完全等效的。但因是标量函数,所以引进静电势对求解静电场更加方便.)(rrϕ2、从势的定义式可以明显看出,电势函数加上一个任意常数并不改变电场的分布,所以我们可以选择任意一点的电势值作为参考。)(rrϕ3、电势叠加原理:在真空中,点电荷q的电场强度为)(144030rrErrrϕπεπε−∇=∇−==rqrq所以点电荷电势rq04)(πεϕ=rr若真空中有一系列点电荷q1,q2,…,qn,总电场强度为)(14)'(4030r'rrrrrrEirrrrrrrrϕπεπε−∇=−−∇=−′−=∑∑iiiiiiqq所以点电荷系的电势∑=∑−=iiiiiq)(14)(0r'rrrrrrrϕπεϕ其中为第i个点电荷单独存在时空间一点的电势)(rriϕ表明:点电荷系的电场中某点的电势,等于各点电荷单独存在时的电场在该点电势的代数和,这就是电势叠加原理,它是电场叠加原理的直接结果。只要给定电荷分布,原则上可以求得电势分布。但有时电荷分布并非完全已知,因此求解静电势问题还需进一步讨论.注意:上面的推导实际上是选取无穷远处为电位参考点。')'(41)(0dVV∫−='rrrrrrrrρπεϕ连续的电荷分布总可看成点电荷系,因此二、泊松方程和边值关系1、泊松方程:静电场可以用一标量函数的梯度来表示,这只反映了它的一部分规律,而它的另一部分规律,则由高斯定理的微分形式决定ρ=⋅∇Dr在均匀各向同性介质中EDrrε=代入得到)(rEϕ−∇=rερϕ−=∇2其中ρ为自由电荷密度。此式称为泊松(Poisson)方程。如果在区域中不存在电荷,方程变为02=∇ϕ此式称为拉普拉斯(Laplace)方程。因此,引入静电势后,就把求解静电场的问题归结为求解静电势所满足的偏微分方程问题。ερϕ/2−=∇2、电势的边值关系:由场的边值关系及和φ所满足的边值关系之一σ=−⋅)(12DDnEDε=ϕ−∇=Eσϕεϕε−=∂∂−∂∂nn1122φ的另一边值关系可直接由得到)()(00PPdPPϕϕ−=⋅∫lE21ϕϕ=这是因为分界面上E有限,而且分界面两边的l和2两点又无限接近,所以式的积分趋于零。说明,电势在分界面处是连续的.∫⋅21PPdlE⎪⎪⎭⎪⎪⎬⎫−=∂∂−∂∂=−=∇σϕεϕεϕϕερϕnn1122212求得φ后,再利用,求得电场E,从而决定了整个电场的分布.用这种方法求解电场分布的简单之处是φ只有一个分量,而不像E有三个分量,因此只需解φ所适合的一个微分方程ϕ−∇=E引进电势φ之后,我们就由下列方程组及边值关系决定φ但是需要进一步讨论的是,这种方法决定的电场是不是唯一的?3、导体表面上的边值关系在静电问题中,常常有一些导体存在,由于导体的特殊性质,在导体表面上的边值关系有它自己的特点.导体的静止条件归结为:(1)导体内部不带电,电荷只能分布于导体表面上;(2)导体内部电场为零;(3)导体表面上电场必沿法线方向,因此导体表面为等势面,整个导体为等势体.常数=ϕσϕε−=∂∂n设导体表面所带电荷面密度为σ,它外面的介质电容率为ε,在导体静电...