SI传染病模型VIP专享VIP免费

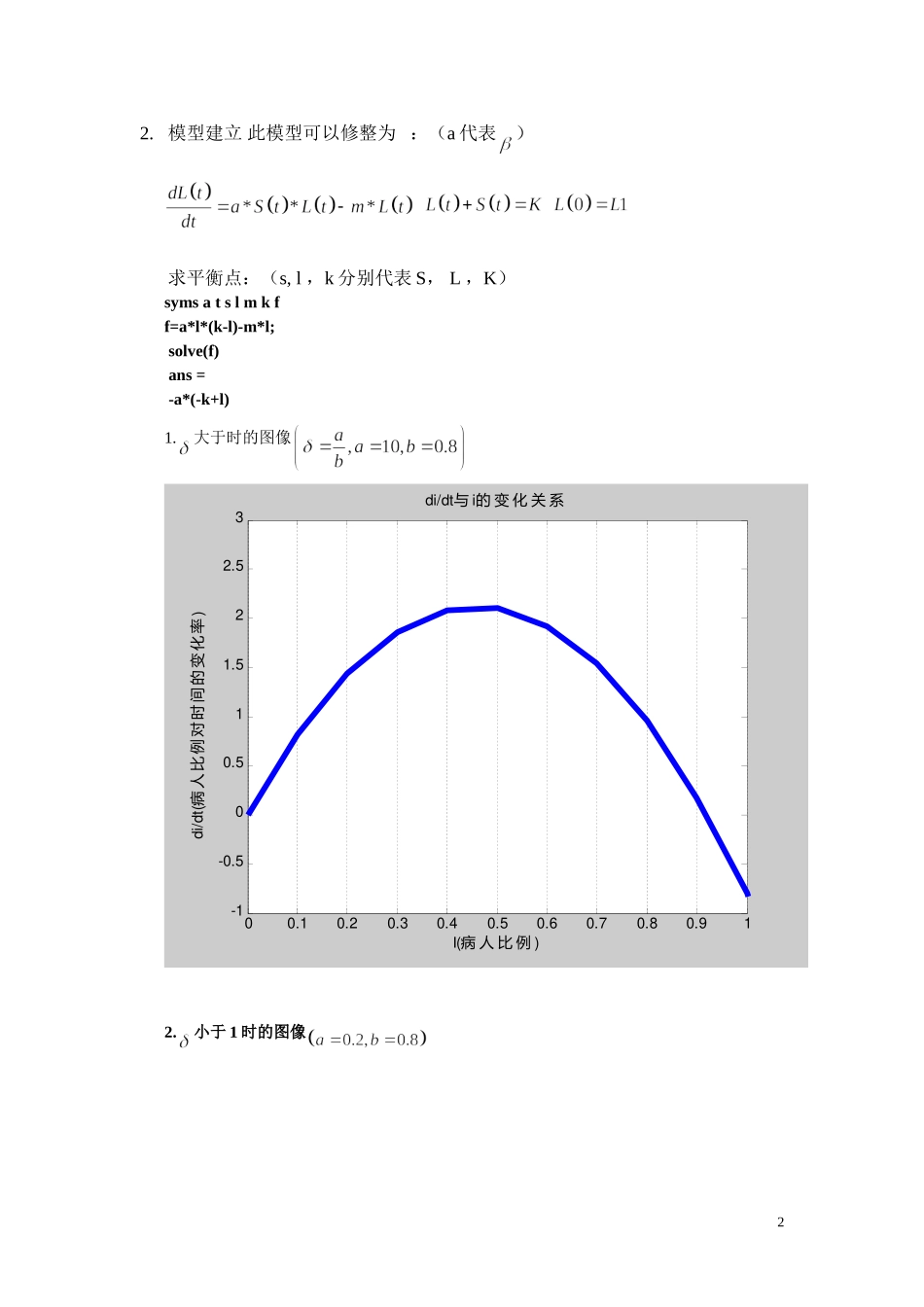
SI传染病模型1.模型的建立由题意知道：在此环境中仅存在健康者（即易感者）和已感者（即病人），且在t时刻人数分别为S(t),L(t),不考虑人口的出生与死亡，此环境中的人口数量不变N即K，于是在单位时间内每天每个病人感染的人数S（t）L（t），它是病人的增加率，所以有：=*S*LL=L1(1)在t时刻健康者与已感者满足关系式：S+L=(2)此模型满足Logistic模型，所以它的解为：L（t）=1/1+((1/L1)-1)*exp(-*t)1.求平衡点symsrSLKyy=r*L*(K-L);solve(y)ans=0SIS传染病模型1.模型假设SIS模型的假设条件1.2与SI模型相同，增加的条件为：每天被治愈的病人数占病人的总数为m，此称为日治愈率。病人治愈后仍然可以成为被感染的健康者，显然，平均传染期为1/m。12.模型建立此模型可以修整为：（a代表）求平衡点：（s,l，k分别代表S，L，K）symsatslmkff=a*l*(k-l)-m*l;solve(f)ans=-a*(-k+l)1.大于时的图像00.10.20.30.40.50.60.70.80.91-1-0.500.511.522.53I()病人比例di/dt()病人比例对时间的变化率di/dti与的变化关系2.小于1时的图像200.20.40.60.811.21.41.61.82-2-1.8-1.6-1.4-1.2-1-0.8-0.6-0.4-0.20i病人比例di/dt()病人比例对时间的比率di/dti与的变化关系data1三．SIR模型模型假设：在SIS模型中我们增加：人群可分为健康者，病人，病疫免疫的移出者，且三种人群的数量分别为S，L，R；病人的日接触率和日治愈率分别为，m所以传染期为1.模型建立(1)(2)求平衡点symsatslmk[s,l]=solve('a*l*(k-l)-m*l','-(a*s*(k-s))')s=a*k-a*la*k-a*ll=0k3健康者与病人数量在总人数中的比例，对时间的变化关系图为：0510152025303540455000.10.20.30.40.50.60.70.80.91时间比例健康者与病人各占比例随时间的变化关系i(t)病人数量占总人数的比例s(t)健康者占总人口的比例健康者与病人各自占总人数的比例间的相互关系：00.050.10.150.20.250.30.350.400.10.20.30.40.50.60.70.80.91病人所占总人数的比例健康者所占总人数的比例i-s的图形（相轨线）健康者与病人各自占总人数的比例间的相互关系4