经典几何中线段和差最值(含答案)VIP免费

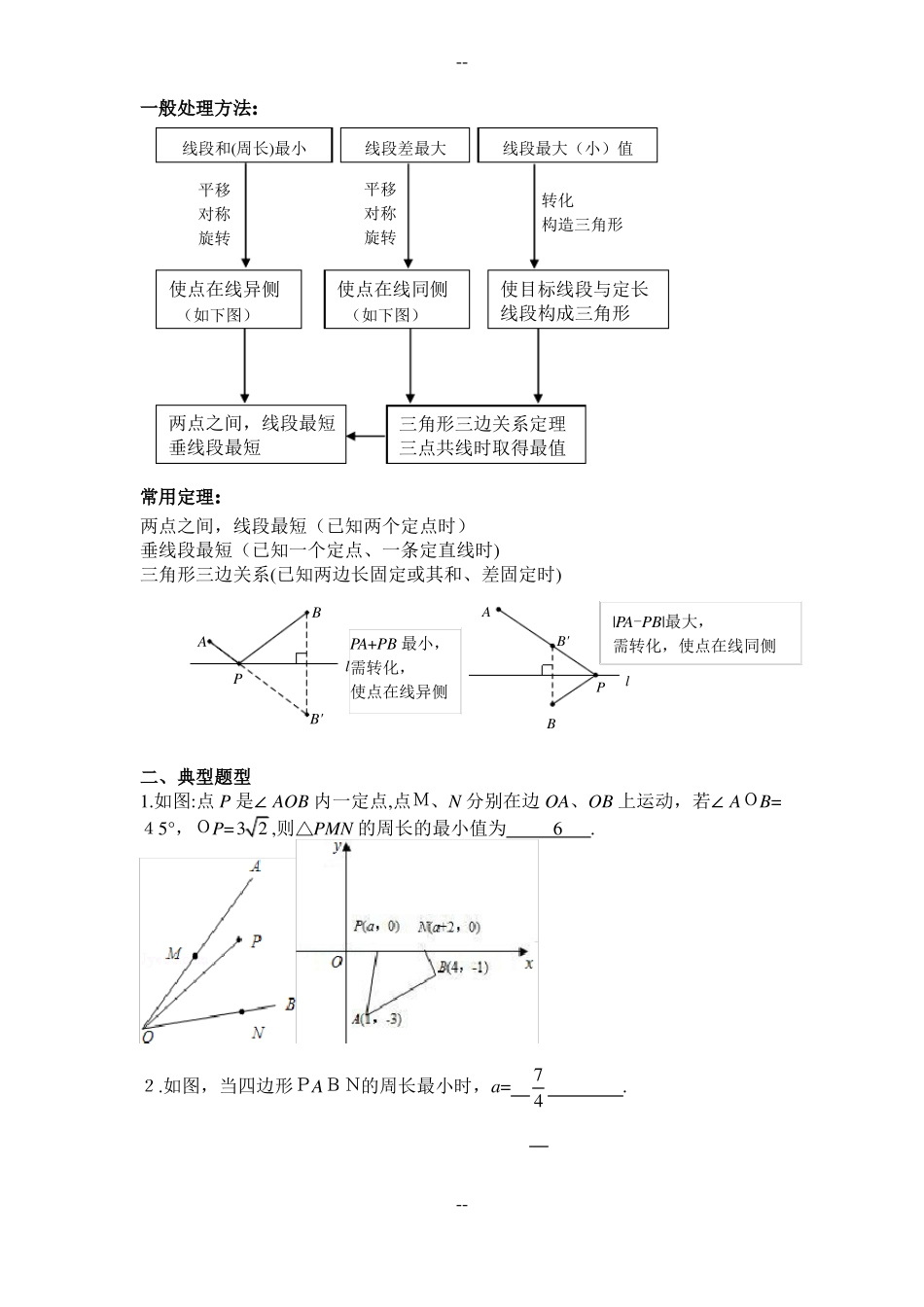
--几何中线段和，差最值问题一、解决几何最值问题的通常思路两点之间线段最短；直线外一点与直线上所有点的连线段中，垂线段最短;三角形两边之和大于第三边或三角形两边之差小于第三边（重合时取到最值）是解决几何最值问题的理论依据，根据不同特征转化是解决最值问题的关键.通过转化减少变量，向三个定理靠拢进而解决问题;直接调用基本模型也是解决几何最值问题的高效手段．几何最值问题中的基本模型举例B图形BAAPlAPlMNl轴原理两点之间线段最短对A,Ｂ为定点,l为定直称最特征线，P为直线l上的一个动点，求AP+值ＢP的最小值B两点之间线段最短三角形三边关系Ａ,B为定点，l为定直Ａ,Ｂ为定点，l为定线,MN为直线l上的一直线，P为直线ｌ上条动线段,求AＭ+BN的一个动点,求的最小值|AP-BP｜的最大值先平移AM或BN使M，作其中一个定点关N重合，然后作其中一作其中一个定点关于转化于定直线ｌ的对称个定点关于定直线ｌ定直线l的对称点点的对称点AM折叠BCN最值原理两点之间线段最短在△ABＣ中，M，N两点分别是边AB，ＢC上的动点，将△BMＮ沿特征ＭＮ翻折，B点的对应点为B'，连接AB',求ＡＢ'的最小值.转化转化成求AＢ'+Ｂ＇N+ＮC的最小值图形B'----一般处理方法:线段和(周长)最小线段差最大线段最大（小）值平移平移转化对称对称构造三角形旋转旋转使点在线同侧使目标线段与定长使点在线异侧（如下图）（如下图）线段构成三角形两点之间，线段最短三角形三边关系定理垂线段最短三点共线时取得最值常用定理:两点之间，线段最短（已知两个定点时）垂线段最短（已知一个定点、一条定直线时)三角形三边关系(已知两边长固定或其和、差固定时)AB|PA-PB|最大，B'APA+PB最小，需转化，使点在线同侧l需转化，PPl使点在线异侧B'B二、典型题型1.如图:点P是∠AOB内一定点,点Ｍ、N分别在边OA、OB上运动，若∠AＯB=４5°，ＯP=32,则△PMN的周长的最小值为6.２.如图，当四边形ＰAＢＮ的周长最小时，a=7.4----３.如图,A、Ｂ两点在直线的两侧，点A到直线的距离AM=4，点Ｂ到直线的距离BＮ=1，且MN=4，Ｐ为直线上的动点，|PA﹣PＢ|的最大值为5．ADMB′NBP4．动手操作:在矩形纸片AＢＣD中，AＢ=３，AD=5．如图所示，折叠纸片,使点A落在BＣ边上的A′处，折痕为PＱ，当点A′在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为２.5．如图，直角梯形纸片ABＣD,AD⊥AB,AB=8,AD＝ＣＤ=4，点Ｅ、F分别在线段AＢ、AＤ上，将△AＥＦ沿EＦ翻折，点A的落点记为P．当P落在直角梯形ABCD内部时,PD的最小值等于45-8．6.如图,∠ＭＯN=90°，矩形ＡBCD的顶点Ａ、Ｂ分别在边OM，OＮ上,当B在边ON上运动时，A随之在ＯM上运动，矩形ABCD的形状保持不变,其中AB＝2，BC＝1，运动过程中,点Ｄ到点O的最大距离为21.----７．如图,线段ＡB的长为4，Ｃ为AB上一动点,分别以AC、BＣ为斜边在AＢ的同侧作等腰直角△AＣD和等腰直角△ＢＣＥ,那么DE长的最小值是2.８.如图,菱形ABCＤ中,AB＝2，∠A=１20°,点Ｐ，Q,Ｋ分别为线段BC，ＣD，BD上的任意一点，则PＫ+QK的最小值为3．9．如图所示,正方形AＢＣD的边长为１，点Ｐ为边BC上的任意一点(可与Ｂ、C重合),分别过Ｂ、C、Ｄ作射线ＡＰ的垂线，垂足分别为B′、Ｃ′、D′，则BＢ′+CＣ′＋DD′的取值范围是2BB′＋CＣ′+DＤ′2．10．如图，菱形ＡＢCD中,∠Ａ=60°,AＢ=3,⊙A、⊙B的半径分别为２和1，P、E、F分别是边ＣＤ、⊙Ａ和⊙B上的动点，则ＰE+PF的最小值是3．11．点Ａ、Ｂ均在由面积为1的相同小矩形组成的网格的格点上，建立平面直角坐标系如图所示.若P是ｘ轴上使得PAPB的值最大的点，Q是y轴上使得QOQ=3．Ａ＋QＢ的值最小的点，则OPAFyAEBMPCOBx第1１题图第１2题图12.如图，在△ABＣ中，AB=６,ＡＣ=8,BC=10,Ｐ为边ＢC上一动点,PＥ⊥AB于Ｅ,PＦ⊥AC于F，Ｍ为EF中点,则ＡM的最小值为__２.４______＿.1３．如图，点P在第一象限,△AＢP是边长为2的等边三角形，当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是＿31_＿_____.若将△ＡBP中边PA的长度改为22,另两边长度不----变，则点Ｐ到...