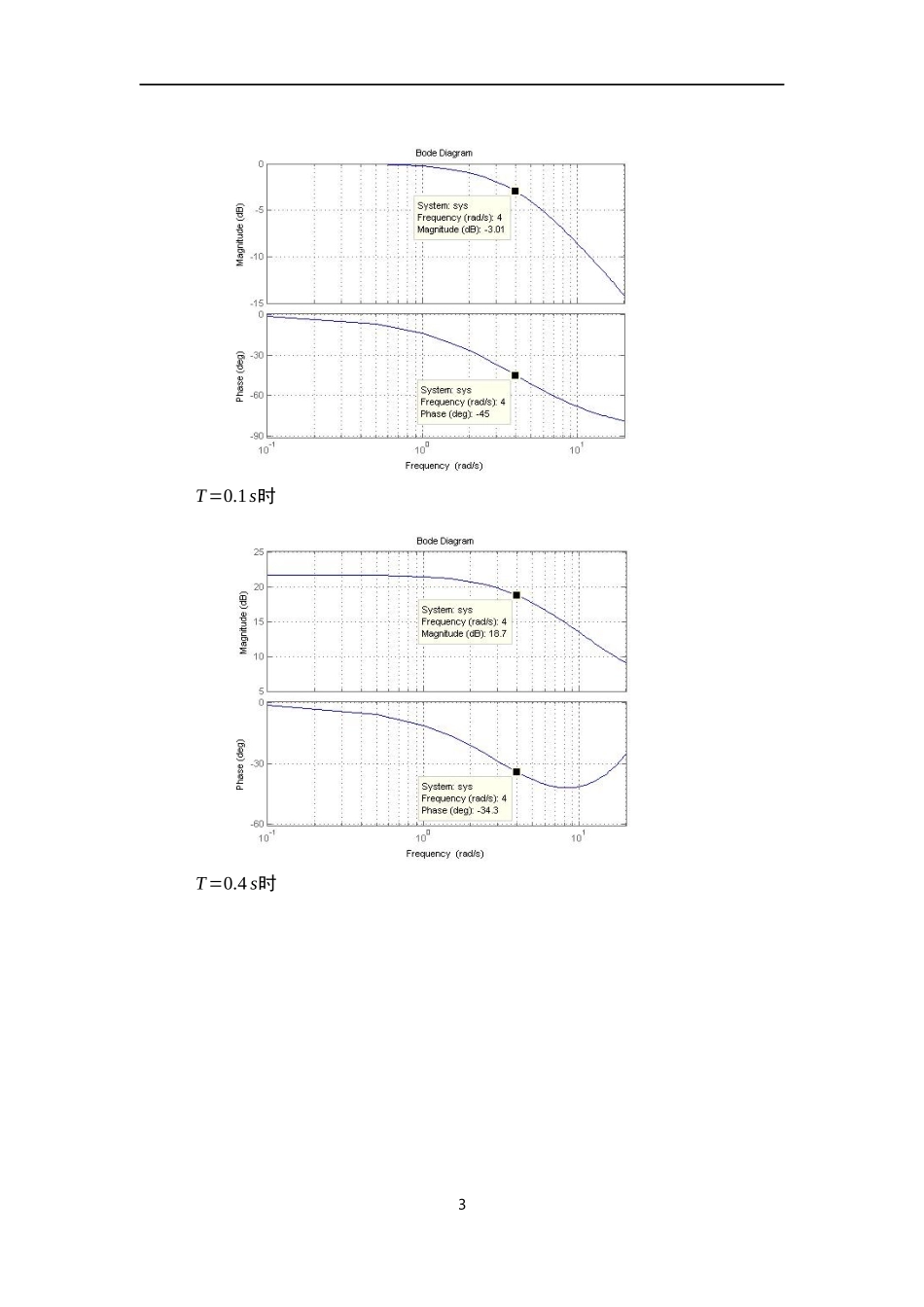
计算机控制系统大作业姓名:陈启航学号:13031144教师:周锐日期:2016年6月1日综合习题1已知:D(s)=4s+4,1)试用Z变换、一阶向后差分、向前差分、零极点匹配、Tustin变换和预修正的Tustin(设关键频率=4)变换等方法将D(s)离散化,采样周期分别取为0.1s和0.4s;2)将D(z)的零极点标在Z平面图上3)计算D(jω)和各个D(ejωT)的幅频和相频特性并绘图,w由0~20rad,计算40个点,应包括=4点,每个T绘一张图(Z变换方法单画)4)计算D(s)及T=0.1,T=0.4时D(z)的单位脉冲响应,运行时间为4秒5)结合所得的结果讨论分析各种离散化方法的特点6)写出报告,附上结果。解:(1)Z变换法:a.离散化:T=0.1s时,D(z)=4zz−0.6703;T=0.4s时,D(z)=4zz−0.2019;b.D(z)的零极点-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81零点T=0.1s时极点T=0.4s时极点c.D(jω)和D(ejωT)幅频相频特性曲线连续系统:2T=0.1s时T=0.4s时3d.D(s)和D(z)单位脉冲响应D(s)单位脉冲响应:D(z)单位脉冲响应:T=0.1s时4T=0.4s时(2)各种离散化方法:a.离散化后的D(z)1、一阶向后差分:T=0.1s时D(z)=0.2857zz−0.7143T=0.4s时D(z)=0.6154zz−0.38462、一阶向前差分:T=0.1s时D(z)=0.4z−0.65T=0.4s时D(z)=1.6z+0.63、零极点匹配T=0.1s时D(z)=0.1648(z+1)z−0.6703T=0.4s时D(z)=0.3991(z+1)z−0.20194、Tustin变换T=0.1s时D(z)=0.1667(z+1)z−0.6667T=0.4s时D(z)=0.4444(z+1)z−0.11115、预修正的Tustin变换(设关键频率=4)T=0.1s时D(z)=0.1685(z+1)z−0.6629T=0.4s时D(z)=0.5073(z+1)z+0.0146b.D(z)的零极点1、一阶向后差分-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81零点T=0.1s时极点T=0.4s时极点2、一阶向前差分6-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81零点T=0.1s时极点T=0.4s时极点3、零极点匹配-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81零点T=0.1s时极点T=0.4s时极点4、Tustin变换-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81零点T=0.1s时极点T=0.4s时极点75、预修正的Tustin变换(设关键频率=4)-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81零点T=0.1s时极点T=0.4s时极点c.D(jω)和D(ejωT)幅频相频特性曲线1、一阶向后差分T=0.1s时T=0.4s时82、一阶向前差分T=0.1s时T=0.4s时93、零极点匹配T=0.1s时T=0.4s时104、Tustin变换T=0.1s时T=0.4s时115、预修正的Tustin变换(设关键频率=4)T=0.1s时T=0.4s时12d.D(s)和D(z)单位脉冲响应1、一阶向后差分T=0.1s时T=0.4s时132、一阶向前差分T=0.1s时T=0.4s时143、零极点匹配T=0.1s时T=0.4s时154、Tustin变换T=0.1s时T=0.4s时165、预修正的Tustin变换(设关键频率=4)T=0.1s时T=0.4s时17二、实验结果分析和总结:在本题中,当采样周期T=0.4s时所有离散方法的都会出现频率混叠现象,使得采样信号失真。因为此采样周期不满足采样定理导致采样信号失真现象。当满足采样定理时,各种离散化方法的特点如下:①Z变换法由Z变换的脉冲响应可看出,连续系统与离散后的系统的脉冲响应相同,故其可以应用在要求脉冲响应不变的场合。但是Z变换容易产生频率混叠,而且变换本身也十分麻烦,在多个环节进行串联时无法单独改变某一串联环节(即无串联性)。②一阶向后差分法稳定性保持不变,无混叠但畸变严重。在采样周期很小的情况下,所得的频率特性与原连续系统的频率特性比较接近但在采样周期较大时相差较大。③一阶向前差分法由于其映射关系,将原系统离散后可能不稳定。但在本题中,系统离散后依然稳定,所以用此方法也可以。在采样周期很小的情况下,所得的频率特性与原连续系统的频率特性比较接近但在采样周期较大时相差较大。④零极点匹配法当D(s)分子阶次低于分母时,D(z)中将带有(z+1)项,可以防止频率混叠,频率保持良好。但在使用单零点匹配时将带来相位的较大延迟,同时,零极点匹配法在使用中要求将稳态增益进行匹配,因此在使用中不是很方便。⑤Tustin变换法采样周期较小的情况下,在低频段范围内,s域与z域的频率近似保...