例1 如图所示,一轻弹簧的右端连着一物体,弹簧的劲度系VIP免费

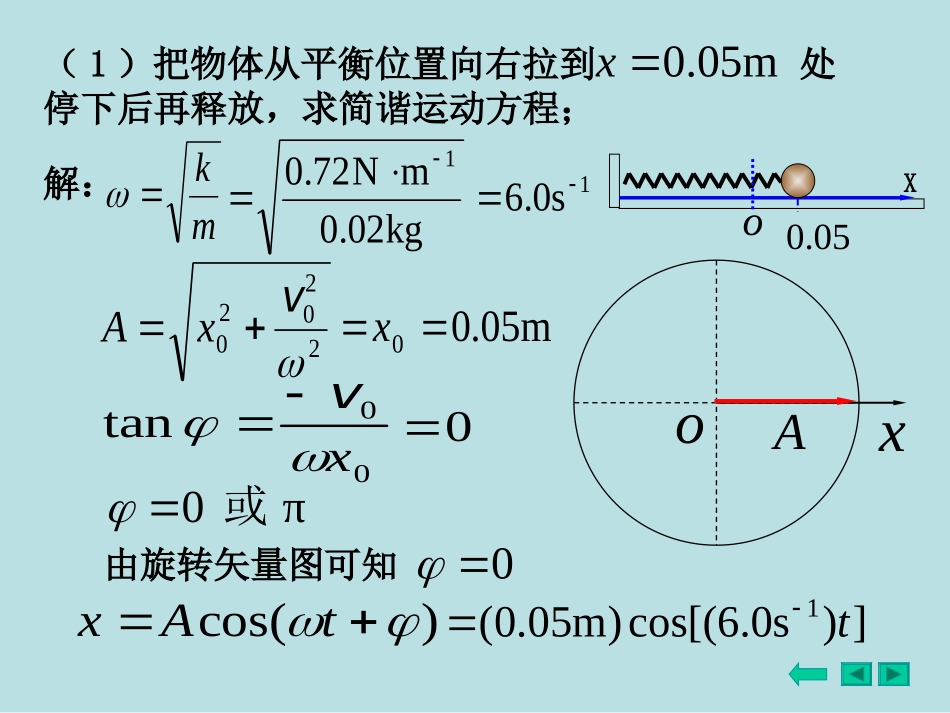
例1如图所示，一轻弹簧的右端连着一物体，弹簧的劲度系数，物体的质量.1mN72.0kg20mm05.0x10sm30.0v（3）若物体在处时速度不等于零，而具有向右的初速度，求其运动方程.2A（2）求物体从初位置运动到第一次经过处时的速度；m/xo0.05m05.0x（1）把物体从平衡位置向右拉到处停下后再释放，求简谐运动方程；)cos(tAxox解：mk22020vxA00tanxvπ0或A由旋转矢量图可知0)cos(tAx])s0.6cos[()m05.0(1tm05.0x（1）把物体从平衡位置向右拉到处停下后再释放，求简谐运动方程；o0.05X11s0.6kg02.0mN72.0m05.00x0oxA2A解:)cos(tAx)cos(tA21)cos(Axt3π53π或tA3πt由旋转矢量图可知tAsinv1sm26.0（负号表示速度沿轴负方向）Ox2A（2）求物体从初位置运动到第一次经过处时的速度；1s0.6m05.0A03π解:22020vxA＇00tanxv＇4π34π或＇ox＇A4π)cos(tAx]4π)s0.6cos[()m0707.0(1tm05.0x10sm30.0v（3）如果物体在处时速度不等于零，而是具有向右的初速度，求其运动方程.因为，由旋转矢量图可知4π＇00v1s0.6m0707.01例2一质量为的物体作简谐运动，其振幅为，周期为，起始时刻物体在kg01.0m08.0s4xm04.0处，向轴负方向运动（如图）.试求Ox（1）时，物体所处的位置和所受的力；s0.1to08.004.004.008.0m/xv解:m08.0A1s2ππ2Tm04.0,0xt代入)cos(tAxcos)m08.0(m04.03π3π00vA3πo08.004.004.008.0m/xv]3π)s2πcos[()m08.0(1txs0.1t代入上式得m069.0xxmkxF2)m069.0()s2π)(kg01.0(21N1070.13kg01.0m3πm08.0A1s2πo08.004.004.008.0m/xv（2）由起始位置运动到处所需要的最短时间.m04.0x法一:设由起始位置运动到处所需要的最短时间为m04.0xt]3π)s2πcos[()m08.0(m04.01ts2π3π)21(arccosts667.0s32]3π)s2πcos[()m08.0(1txo08.004.004.008.0m/x法二:3π3π起始时刻时刻tt3πts667.0s32t1s2π例3一质点沿x轴作简谐振动，振幅为12cm，周期为2s。当t=0时,位移为6cm，且向x轴正方向运动。求⑴振动方程。⑵t=0.5s时，质点的位置、速度和加速度。⑶如果某时刻质点位于x=-6cm，且向x轴负方向运动，求从该位置回到平衡位置所需要的时间。解：⑴设简谐振动方程为已知：A=12cm,T=2s12sTt=0时,x0=0.06m,v0>0)cos(tAx)cos(120tx33cos120060ox3π21cos5.05.0ttdtdxv5.05.0ttdtdva振动方程：)3cos(12.0tx已知A=12cm31s5.05.0)3cos(12.0tttx⑵t=0.5s时，质点的位置、速度和加速度m039.115.0189.0)3sin(12.0smtt25.02103.0)3cos(12.0smtt)3(cos12.006.01t21)3(cos1t343231或tstt132311⑶某时刻ｔ1质点位于x=-6cm，且向x轴负方向运动v <0)3cos(12.0tx振动方程：求从该位置回到平衡位置所需要的时间。stt61123322sttt65161112t2时刻质点回到平衡位置x=0,且v>0法一：vo12.006.012.0xvt2时刻质点回到平衡位置x=0tyx3223ｔ1时刻质点位于x=-6cm，且向x轴负方向运动-A/2)3cos(12.0tx振动方程：653223s6565法二：例4劲度系数为k的轻弹簧，上端固定，下端悬挂质量为m的物体，平衡时弹簧伸长x0，用手向下拉物体，然后无初速释放，证明物体作谐振动，并求振动周期。xoxx0解：设平衡位置为坐标原点平衡时0kxmgkxxxkmgF)(0在任意位置x时，受合力kxmaxmkdtxd220222xdtxdmkgxkmT0222或者则竖直方向运动的弹簧振子做谐振动mgfmgf例5质量为的物体，以振幅作简谐运动，其最大加速度...