统计案例回归分析VIP免费

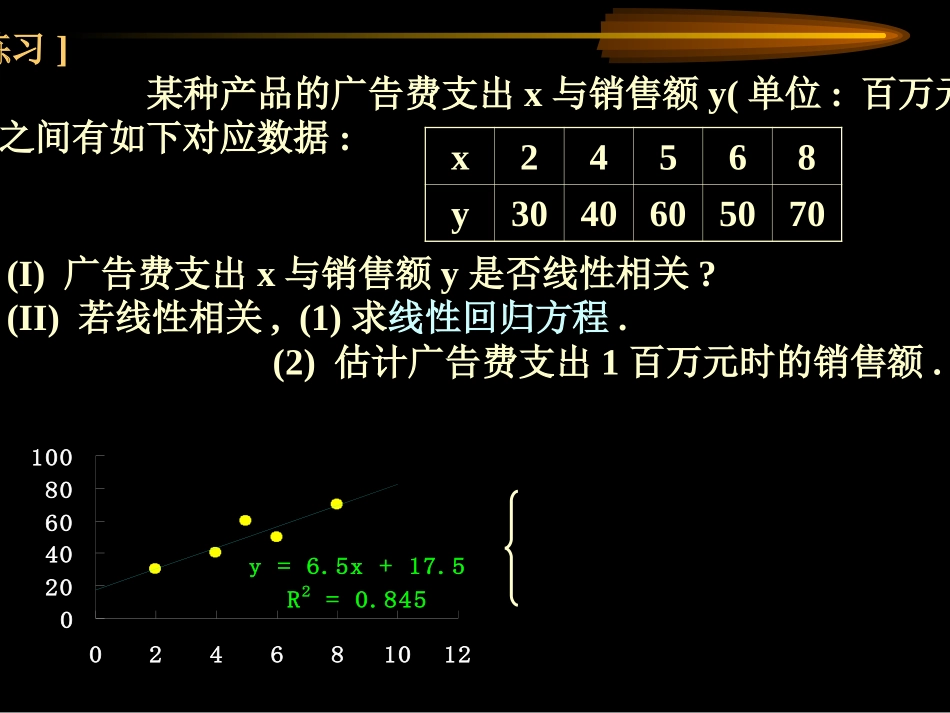
回归分析:是对具有相关关系的两个变量进行统计分析.得到的线性回归方程可用于预测、估计,为决策提供依据.回归分析的步骤:(1)画出散点图；(2)求线性回归方程.(3)用回归直线方程进行预测.一般地，设具有线性相关关系的n对数据(xi,yi)如下：xx1x2x3…xnyy1y2y3…ynn1i2in1iii)xx()yy)(xx(bxbya其线性回归方程中的a,b的最小二乘估计公式:abxyˆ2n1iin1i2in1iin1iin1iii]x[xn]y][x[yxnabxyˆ[练习]某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:x24568y3040605070(I)广告费支出x与销售额y是否线性相关?(II)若线性相关,(1)求线性回归方程.(2)估计广告费支出1百万元时的销售额.0204060800246810y=6.5x+17.5R2=0.8450204060801000246810125.17x5.6yˆxbya2n1iin1i2in1iin1iin1iii]x[xn]y][x[yxnb(I)高考上线人数y与年份x是否线性相关?(II)若线性相关,(1)求线性回归方程.(2)试根据所给数据，预测第5年年高考上线人数.xbya2n1iin1i2in1iin1iin1iii]x[xn]y][x[yxnb年份1234高考上线人数116172220260[练习]某中学由于不断深化教改,办学质量逐年提高.前4年的高考上线人数如下：例1.从某大学中随机选取8名女大学生,其身高和体重数据如表:编号12345678身高/cm165165157170175165155170体重/kg4857505464614359求根据一名女大学生的身高预报她的体重的回归方程，并预报一名身高为172cm的女大学生的体重.40455055606570150155160165170175180y=0.8485x-85.71240455055606570150155160165170175180xbya2n1iin1i2in1iin1iin1iii]x[xn]y][x[yxnb712.85x849.0yˆ故对于身高为172cm的女大学生，可预报其体重为60.316kg目的求根据一名女大学生的身高预报她的体重的回归方程，并预报一名身高为172cm的女大学生的体重.体重为60.316kg[思考]身高为172cm的女大学生体重一定是60.316kg吗？若不是，其原因是什么？接近于由于所有的样本点不共线，而只是散布在某一直线附近,故线性函数模型只能近似地刻画身高与体重的之间的关系.y=0.8485x-85.71240455055606570150155160165170175180712.85x849.0yˆ不能用一次函数来严格刻画!60.316kg为身高为172cm的女大学生的平均体重的估计值.(非真实体重)求根据一名女大学生的身高预报她的体重的回归方程，并预报一名身高为172cm的女大学生的体重.体重为60.316kg[思考]身高为172cm的女大学生体重一定是60.316kg吗？若不是，其原因是什么？接近于由于所有的样本点不共线，而只是散布在某一直线附近，y=bx+a+ey=0.8485x-85.71240455055606570150155160165170175180712.85x849.0yˆy=bx+a+e(a,b为模型的未知参数,e是y与之间的误差)随机误差0De0Ee2预报变量解释变量故身高和体重的关系可用下面的线性回归模型来表示：abxy~线性函数模型身高和体重的关系可用下面的线性回归模型来表示：y=bx+a+e(a,b为模型的未知参数,e是y与之间的随机误差)0De,0Ee2随机误差e是引起预报值与真实值y之间的误差的原因之一,其大小取决于其方差.yˆabxy~随机误差e的方差2越小,通过预报真实值y的精确越高.~y[思考]随机误差e是预报真实值y的误差，是一个不可观测的量,那应该怎样研究e？如何衡量预报的精确度？y~随机变量数字特征：均值、方差.40455055606570150155160165170175180aˆxbˆyˆy~ye[思考]随机误差e是预报真实值y的误差，是一个不可观测的量,那应该怎样研究e？如何衡量预报的精确度？y~(方差2)yˆyeˆ估计称为相应于点(xi,yi)的残差.iiiyˆyeˆn1i2ieˆ)bˆ,aˆ(Q称为残差平方和.n1i2i2eˆ2n1ˆ在研究两变量间的关系时，首先要根据散点图来粗略判断它们是否线性相关，是否可用线性回归模型来拟合数据.然后可通过残差来判断模型拟合的效果，判断原始数据中是否存在可疑数据.ieˆ残差分析5943616454505748体重/kg170155165175170157165165身高/cm87654321编号0.382-2.8836.6271.137-4.6182.4192.627-6.373残...