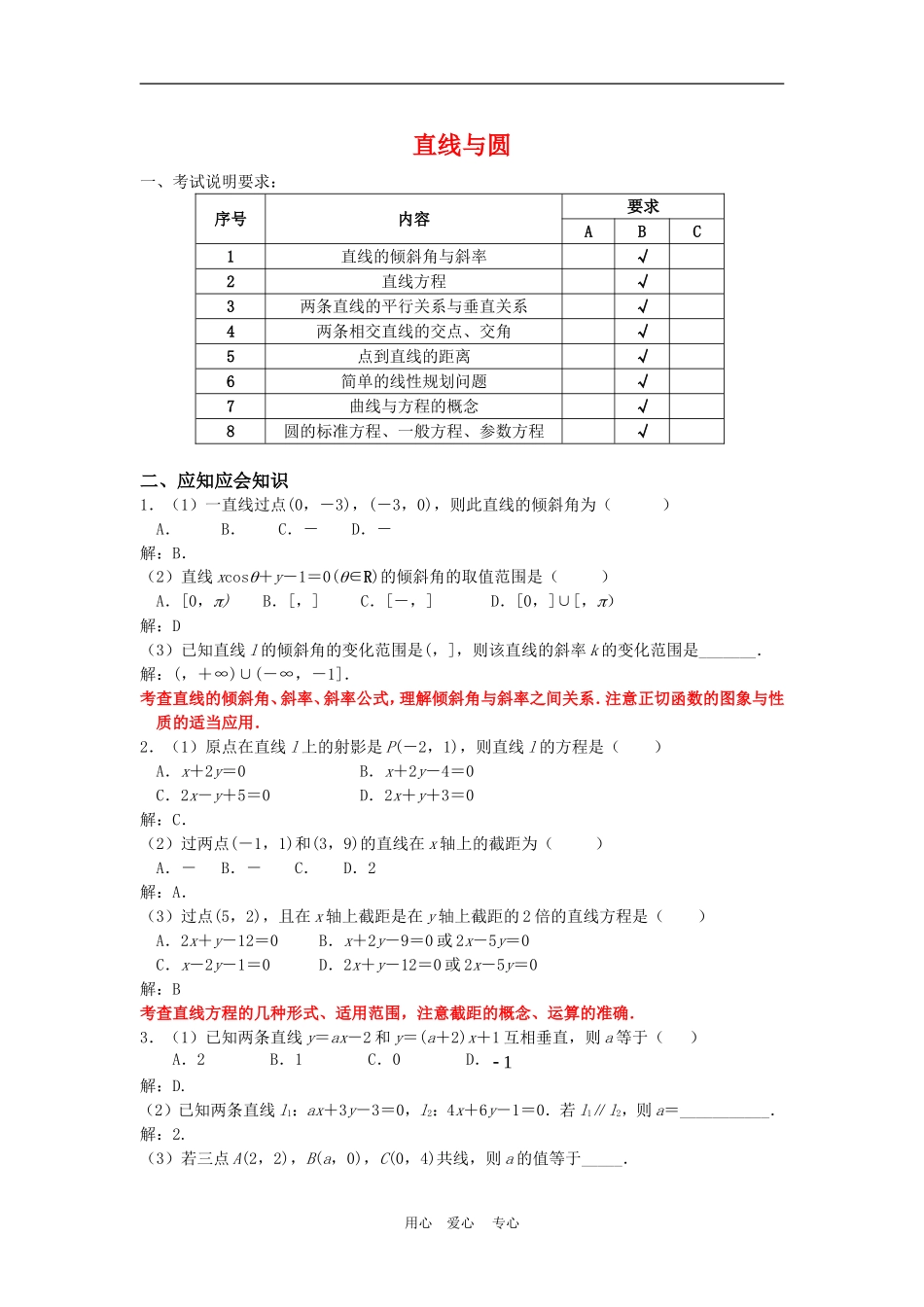
直线与圆一、考试说明要求:序号内容要求ABC1直线的倾斜角与斜率√2直线方程√3两条直线的平行关系与垂直关系√4两条相交直线的交点、交角√5点到直线的距离√6简单的线性规划问题√7曲线与方程的概念√8圆的标准方程、一般方程、参数方程√二、应知应会知识1.(1)一直线过点(0,-3),(-3,0),则此直线的倾斜角为()A.B.C.-D.-解:B.(2)直线xcosq+y-1=0(q∈R)的倾斜角的取值范围是()A.[0,p)B.[,]C.[-,]D.[0,]∪[,p)解:D(3)已知直线l的倾斜角的变化范围是(,],则该直线的斜率k的变化范围是_______.解:(,+∞)∪(-∞,-1].考查直线的倾斜角、斜率、斜率公式,理解倾斜角与斜率之间关系.注意正切函数的图象与性质的适当应用.2.(1)原点在直线l上的射影是P(-2,1),则直线l的方程是()A.x+2y=0B.x+2y-4=0C.2x-y+5=0D.2x+y+3=0解:C.(2)过两点(-1,1)和(3,9)的直线在x轴上的截距为()A.-B.-C.D.2解:A.(3)过点(5,2),且在x轴上截距是在y轴上截距的2倍的直线方程是()A.2x+y-12=0B.x+2y-9=0或2x-5y=0C.x-2y-1=0D.2x+y-12=0或2x-5y=0解:B考查直线方程的几种形式、适用范围,注意截距的概念、运算的准确.3.(1)已知两条直线y=ax-2和y=(a+2)x+1互相垂直,则a等于()A.2B.1C.0D.1解:D.(2)已知两条直线l1:ax+3y-3=0,l2:4x+6y-1=0.若l1∥l2,则a=___________.解:2.(3)若三点A(2,2),B(a,0),C(0,4)共线,则a的值等于_____.用心爱心专心解:4(4)与直线3x-4y+5=0共线的单位向量是()A.(3,4)B.(4,-3)C.(,)D.(,)解:D.(5)a=3是直线ax+2y+3a=0和直线3x+(a-1)y=a-7平行且不重合的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件解:C.(6)直线x+a2y+1=0与直线(a2+1)x-by+3=0互相垂直,ab∈R,则||ab|的最小值是()A.1B.2C.4D.5解:B.考查两条直线平行与垂直的条件,注意选择合理的转化方法.4.(1)直线y=2与直线x+y—2=0的夹角是()A.B.C.D.解:A.(2)若直线l:y=kx-与直线2x+3y-6=0交点位于第一象限,则直线l的倾斜角的取值范围是()A.[,)B.(,)C.(,)D.[,)解:B.考查两条直线的交点与夹角的计算,注意运算准确.5.(1)已知点(a,2)(a>0)到直线l:x-y+3=0的距离为1,则a等于()A.B.2-C.-1D.+1解:C.(2)已知实数x,y满足2x+y+5=0,那么的最小值为()A.B.C.2D.2解:A.(3)直线y=2x关于x轴对称的直线方程为()A.y=-xB.y=xC.y=-2xD.y=2x解:C.(4)若点P(3,4)、Q(a,b)关于直线x-y-1=0对称,则()A.a=1,b=-2B.a=2,b=-1C.a=4,b=3D.a=5,b=2解:D.考查点到直线的距离公式,注意综合应用平行、垂直、夹角、交点、距离等工具转化对称问题.6.(1)不等式组表示的平面区域的面积是()A.48B.36C.24D.12解:C(2)图中阴影部分用二元一次不等式组表示为__________________.用心爱心专心xyO2-1-1解:(3)设z=2y-x,式中变量x,y满足条件则z的最大值为_________.解:11.(4)已知平面区域D由以A(1,3),B(5,2),C(3,1)为顶点的三角形内部以及边界组成.若在区域D上有无穷多个点(x,y)可使目标函数z=x+my取得最小值,则m=()A.-2B.-1C.1D.4解:C.(5)某公司招收男职员x名,女职员y名,x和y须满足约束条件则z=10x+10y的最大值是()A.80B.85C.90D.95解:C.考查线性规划问题,注意平面区域与不等式组的对应,体会数形结合的重要思想.7.(1)以点(1,2)为圆心,与直线4x+3y-35=0相切的圆的方程是___________.解:(x-1)2+(y-2)2=25.(2)圆心在直线y=x上且与x轴相切于点(1,0)的圆的方程为.解:(x-1)2+(y-1)2=1.(3)过点A(1,-1),B(-1,1)且圆心在直线x+y-2=0上的圆的方程是()A.(x-3)2+(y+1)2=4B.(x+3)2+(y-1)2=4C.(x-1)2+(y-1)2=4D.(x+1)2+(y+1)2=4解:C.考查圆的方程,注意直接找圆心、半径与待定系数法之间的关系...