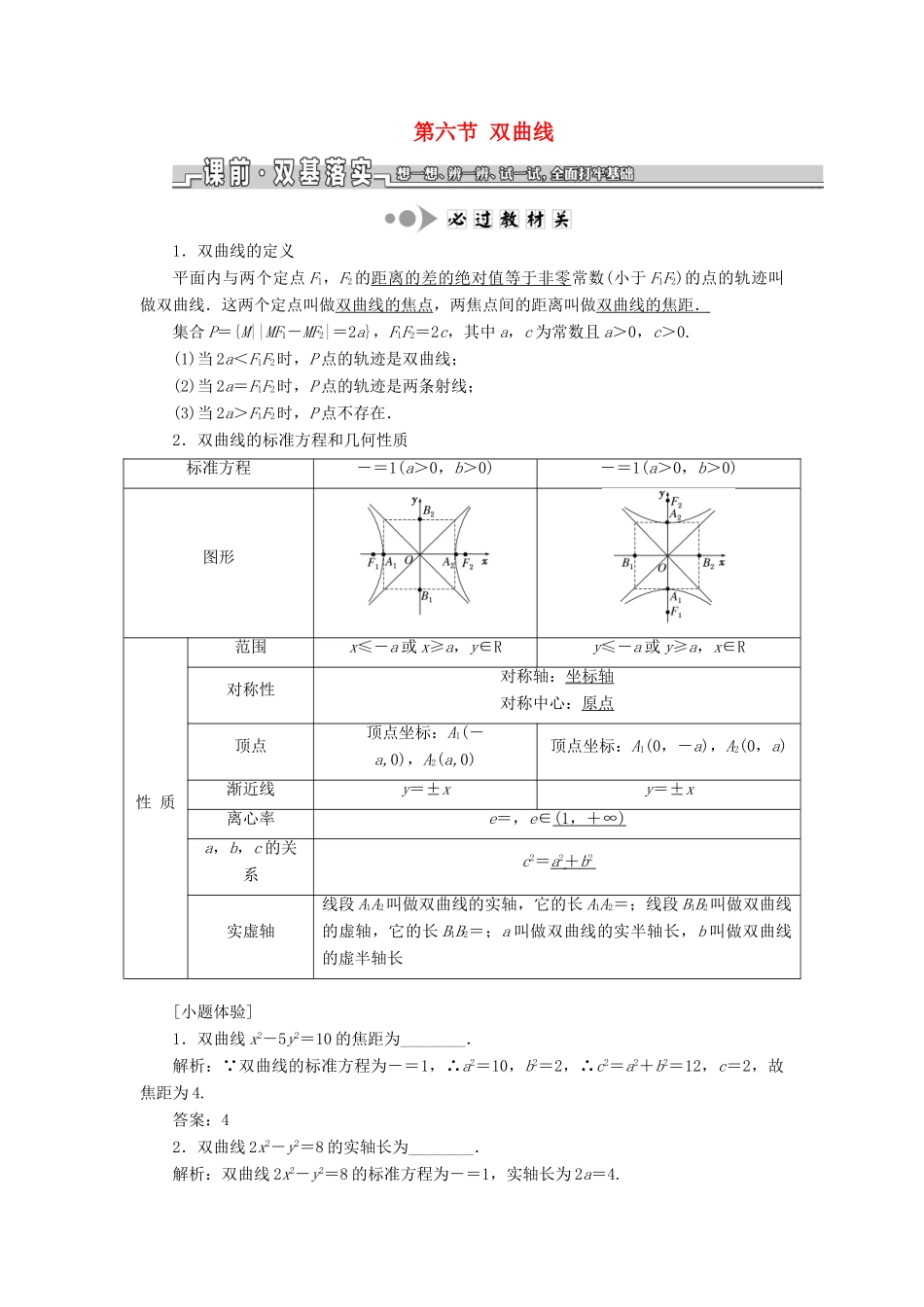
第六节双曲线1.双曲线的定义平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于F1F2)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.集合P={M||MF1-MF2|=2a},F1F2=2c,其中a,c为常数且a>0,c>0.(1)当2a<F1F2时,P点的轨迹是双曲线;(2)当2a=F1F2时,P点的轨迹是两条射线;(3)当2a>F1F2时,P点不存在.2.双曲线的标准方程和几何性质标准方程-=1(a>0,b>0)-=1(a>0,b>0)图形性质范围x≤-a或x≥a,y∈Ry≤-a或y≥a,x∈R对称性对称轴:坐标轴对称中心:原点顶点顶点坐标:A1(-a,0),A2(a,0)顶点坐标:A1(0,-a),A2(0,a)渐近线y=±xy=±x离心率e=,e∈(1,+∞)a,b,c的关系c2=a2+b2实虚轴线段A1A2叫做双曲线的实轴,它的长A1A2=;线段B1B2叫做双曲线的虚轴,它的长B1B2=;a叫做双曲线的实半轴长,b叫做双曲线的虚半轴长[小题体验]1.双曲线x2-5y2=10的焦距为________.解析: 双曲线的标准方程为-=1,∴a2=10,b2=2,∴c2=a2+b2=12,c=2,故焦距为4.答案:42.双曲线2x2-y2=8的实轴长为________.解析:双曲线2x2-y2=8的标准方程为-=1,实轴长为2a=4.答案:43.已知双曲线-=1的右焦点为(3,0),则该双曲线的离心率等于________.解析: 右焦点为(3,0),∴c=3.∴a2=c2-b2=9-5=4,∴a=2,∴e==.答案:1.双曲线的定义中易忽视2a<F1F2这一条件.若2a=F1F2,则轨迹是以F1,F2为端点的两条射线,若2a>F1F2,则轨迹不存在.2.双曲线的标准方程中对a,b的要求只是a>0,b>0,易误认为与椭圆标准方程中a,b的要求相同.若a>b>0,则双曲线的离心率e∈(1,);若a=b>0,则双曲线的离心率e=;若0<a<b,则双曲线的离心率e∈(,+∞).3.注意区分双曲线中的a,b,c大小关系与椭圆中的a,b,c关系,在椭圆中a2=b2+c2,而在双曲线中c2=a2+b2.4.易忽视渐近线的斜率与双曲线的焦点位置关系.当焦点在x轴上,渐近线斜率为±,当焦点在y轴上,渐近线斜率为±.[小题纠偏]1.设P是双曲线-=1上一点,F1,F2分别是双曲线左、右两个焦点,若PF1=9,则PF2等于________.解析:由题意知PF1=9<a+c=10,所以P点在双曲线的左支,则有PF2-PF1=2a=8,故PF2=PF1+8=17.答案:172.若a>1,则双曲线-y2=1的离心率的取值范围是________.解析:由题意得双曲线的离心率e=.即e2==1+.因为a>1,所以0<<1,所以1<1+<2,所以1<e<.答案:(1,)3.离心率为,且经过(-,2)的双曲线的标准方程为________.解析:当双曲线的焦点在x轴上时,设方程为-=1.则有解得所以所求双曲线的标准方程为x2-=1.当双曲线焦点在y轴上时,设方程为-=1.则有解得所以所求双曲线的标准方程为-=1.答案:x2-=1或-=1[题组练透]1.若方程+=1(k∈R)表示双曲线,则k的取值范围是________.解析:依题意可知(k-3)(k+3)<0,解得-3<k<3.答案:(-3,3)2.已知双曲线C:-=1的离心率e=,且其右焦点为F2(5,0),则双曲线C的标准方程为________.解析:因为所求双曲线的右焦点为F2(5,0)且离心率为e==,所以c=5,a=4,b2=c2-a2=9,所以所求双曲线的标准方程为-=1.答案:-=13.若以F1(-,0),F2(,0)为焦点的双曲线过点(2,1),则该双曲线的标准方程为________.解析:依题意,设题中的双曲线方程是-=1(a>0,b>0),则有解得a2=2,b2=1.因此该双曲线的标准方程是-y2=1.答案:-y2=14.(2019·苏锡常镇调研)已知双曲线Γ过点(2,),且与双曲线-y2=1有相同的渐近线,则双曲线Γ的标准方程为________.解析:依题意,设所求双曲线的标准方程为-y2=λ,将点(2,)的坐标代入,得1-3=λ,∴λ=-2,∴所求双曲线的方程为-y2=-2,其标准方程为-=1.答案:-=1[谨记通法]求双曲线标准方程的一般方法(1)待定系数法:设出双曲线方程的标准形式,根据已知条件,列出参数a,b,c的方程并求出a,b,c的值.与双曲线-=1有相同渐近线时,可设所求双曲线方程为-=λ(λ≠0).(2)定义法:依定义得出距离之差的等量关系式,求出a的值,由定点位置确定c的值.[典例引...