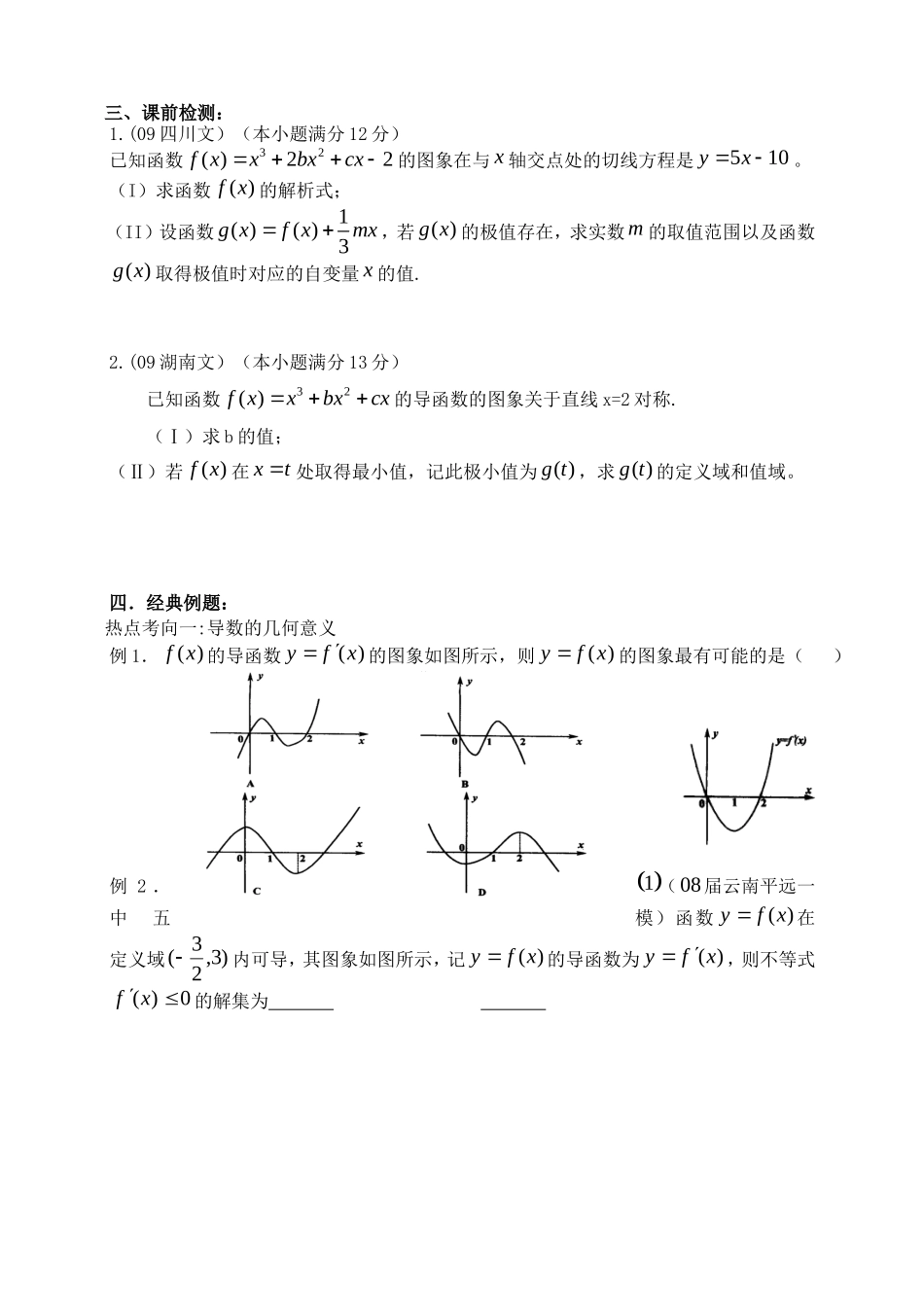
2.16导数的应用一、学习目标:考纲点击:1.理解可导函数的单调性与其导数的关系;2.了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);3.会求一些实际问题(一般指单峰函数)的最大值和最小值.热点提示:导数的应用已成为高考必考点,重点考查利用导数研究函数的单调性,求单调区间、极值、最值,以及利用导数解决生活中优化问题,可以与解析几何、不等式、平面向量等知识交汇命题。多以解答题出现,属中高档题。二、知识要点:1.利用导数研究多项式函数单调性的一般步骤:1求()fx;2确定()fx在,ab内符号;3若()0fx在,ab上恒成立,则()fx在,ab上是增函数;若()0fx在,ab上恒成立,则()fx在,ab上是减函数新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆①()0fx()fx为增函数(()0fx()fx为减函数).②()fx在区间,ab上是增函数()fx≥0在,ab上恒成立;()fx在区间,ab上为减函数()fx≤0在,ab上恒成立.2.极大值:一般地,设函数()fx在点0x附近有定义,如果对0x附近的所有的点,都有0()()fxfx,就说0()fx是函数()fx的一个极大值,记作y极大值0()fx,0x是极大值点.3.极小值:一般地,设函数()fx在0x附近有定义,如果对0x附近的所有的点,都有0()()fxfx就说0()fx是函数()fx的一个极小值,记作y极小值0()fx,0x是极小值点。4.求可导函数()fx的极值的步骤:1确定函数的定义区间,求导数)(xf2求方程()0fx的根奎屯王新敞新疆3用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查)(xf在方程根左右的值的符号,如果左正右负,那么()fx在这个根处取得极大值;如果左负右正,那么()fx在这个根处取得极小值;如果左右不改变符号,那么()fx在这个根处无极值.如果函数在某些点处连续但不可导,也需要考虑这些点是否是极值点.5.函数的最大值和最小值:一般地,在闭区间ba,上连续的函数)(xf在ba,上必有最大值与最小值.6.利用导数求函数的最值步骤:由上面函数)(xf的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了.设函数)(xf在ba,上连续,在(,)ab内可导,则求)(xf在ba,上的最大值与最小值的步骤如下:1求)(xf在(,)ab内的极值;2将)(xf的各极值与)(af、)(bf比较得出函数)(xf在ba,上的最值奎屯王新敞新疆p7.求参数范围的方法:①分离变量法;②构造(差)函数法.8.通过求导求函数不等式的基本思路是:以导函数和不等式为基础,单调性为主线,最(极值)为助手,从数形结合、分类讨论等多视角进行综合探索.三、课前检测:1.(09四川文)(本小题满分12分)已知函数32()22fxxbxcx的图象在与x轴交点处的切线方程是510yx。(I)求函数()fx的解析式;(II)设函数1()()3gxfxmx,若()gx的极值存在,求实数m的取值范围以及函数()gx取得极值时对应的自变量x的值.2.(09湖南文)(本小题满分13分)已知函数32()fxxbxcx的导函数的图象关于直线x=2对称.(Ⅰ)求b的值;(Ⅱ)若()fx在xt处取得最小值,记此极小值为()gt,求()gt的定义域和值域。四.经典例题:热点考向一:导数的几何意义例1.()fx的导函数()yfx的图象如图所示,则()yfx的图象最有可能的是()例2.1(08届云南平远一中五模)函数)(xfy在定义域)3,23(内可导,其图象如图所示,记)(xfy的导函数为)(xfy,则不等式0)(xf的解集为(2)设(),()fxgx均是定义在R上的奇函数,当0x时,()()fxgx()()0fxgx,且(2)0f,则不等式()()0fxgx的解集是热点考向二:函数的极值,最值以及恒成立问题例3:函数Rxxxxf,56)(3,(Ⅰ)求)(xf的单调区间和极值;(Ⅱ)若关于x的方程axf)(有3个不同实根,求实数a的取值范围.(Ⅲ)已知当(1,)x时,()fx≥(1)kx恒成立,求实数k的取值范围.例4;已知定义在正实数集上的函数21()22fxxax,2()3lngxaxb,其中...