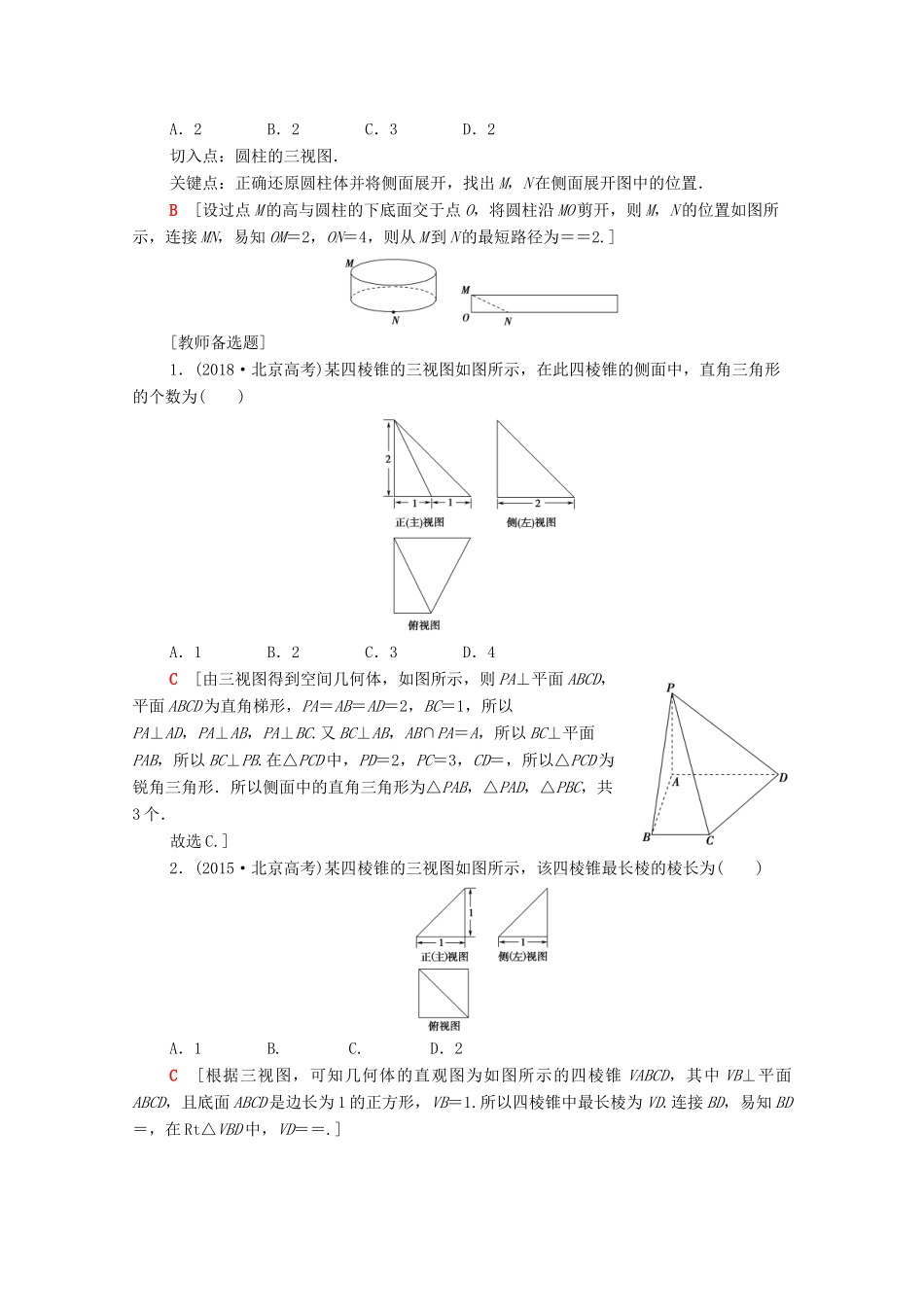
第1讲空间几何体的表面积、体积及有关量的计算[做小题——激活思维]1.一个球的表面积是16π,那么这个球的体积为()A.πB.πC.16πD.24πB[设球的半径为R,则由4πR2=16π,解得R=2,所以这个球的体积为πR3=π.]2.如图,已知正三棱柱ABCA1B1C1中,AB=,AA1=4,若点P从点A出发,沿着正三棱柱的表面,经过棱A1B1运动到点C1,则点P运动的最短路程为()A.5B.C.4D.6B[将三棱柱展开成如图的图形,让点C1与ABB1A1在同一平面内,C1D⊥AB交A1B1于Q,则C1Q⊥A1B1,∴A1Q=AD=,两点之间线段最短,故AC1即为所求的最短距离,因为C1Q=A1C1×sin60°=×=,所以C1D=+4=,AD=,所以AC1===.]3.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为________,体积为________.28π16π+π[由三视图知该几何体是圆锥与圆柱的组合体,设圆柱底面圆半径为r,周长为c,圆锥母线长为l,圆柱高为h.由图得r=2,c=2πr=4π,h=4,由勾股定理得:l==4,S表=πr2+ch+cl=4π+16π+8π=28π.V=V柱+V锥=16π+π.]4.如图,正三棱柱ABCA1B1C1的底面边长为2,侧棱长为,D为BC的中点,则三棱锥A-B1DC1的体积为________.1[在正三棱柱ABCA1B1C1中, AD⊥BC,AD⊥BB1,BB1∩BC=B,∴AD⊥平面B1DC1.∴VAB1DC1=S△B1DC1·AD=××2××=1.]5.已知一个圆台的下底面半径为3,高为2,当圆台的上底面半径r′变化时,圆台体积的变化范围是________.(6π,18π)[V圆台=π(r2+rr′+r′2)h,0<r′<3.当上底面面积为0时,圆台变为圆锥,V圆锥=πr2h=6π;当r′=3时,圆台变为圆柱,V圆柱=πr2h=18π.所以圆台体积的变化范围是.][扣要点——查缺补漏]1.空间几何体的表面积与体积(1)求三棱锥的体积时,等体积转化是常用的方法,转化原则是其高易求,底面放在已知几何体的某一面上,如T4.(2)求不规则几何体的体积,常用分割或补形的思想,将不规则几何体转化为规则几何体以易于求解.(3)已知几何体的三视图,可去判断几何体的形状和各个度量,然后求解表面积和体积,如T3.2.柱、锥、台之间的关系3.多面体与球(1)设球的半径为R,球的截面圆半径为r,球心到球的截面的距离为d,则有r=.(2)当球内切于正方体时,球的直径等于正方体的棱长,当球外接于长方体时,长方体的体对角线长等于球的直径;当球与正方体各棱都相切时,球的直径等于正方体底面的对角线长.(3)若正四面体的棱长为a,则正四面体的外接球半径为a,内切球半径为a.空间几何体的三视图、展开图、截面图(5年2考)[高考解读]重点考查考生的识图能力和空间想象能力、考生对试题的研究必须经历从“识图”、“想图”到“构图”的过程,要通过观察、分析、想象、判断、计算的逻辑思维才能求解,考查了考生的直观想象和逻辑推理的核心素养.(2018·全国卷Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.2B.2C.3D.2切入点:圆柱的三视图.关键点:正确还原圆柱体并将侧面展开,找出M,N在侧面展开图中的位置.B[设过点M的高与圆柱的下底面交于点O,将圆柱沿MO剪开,则M,N的位置如图所示,连接MN,易知OM=2,ON=4,则从M到N的最短路径为==2.][教师备选题]1.(2018·北京高考)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()A.1B.2C.3D.4C[由三视图得到空间几何体,如图所示,则PA⊥平面ABCD,平面ABCD为直角梯形,PA=AB=AD=2,BC=1,所以PA⊥AD,PA⊥AB,PA⊥BC.又BC⊥AB,AB∩PA=A,所以BC⊥平面PAB,所以BC⊥PB.在△PCD中,PD=2,PC=3,CD=,所以△PCD为锐角三角形.所以侧面中的直角三角形为△PAB,△PAD,△PBC,共3个.故选C.]2.(2015·北京高考)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A.1B.C.D.2C[根据三视图,可知几何体的直观图为如图所示的四棱锥VABCD,其中VB⊥平面ABCD,且底面ABCD是边长为1的正方形,VB=1.所以四棱锥中最长棱为VD.连接BD,易知BD=,在Rt△VBD中,VD==.]1.由三视图还原...