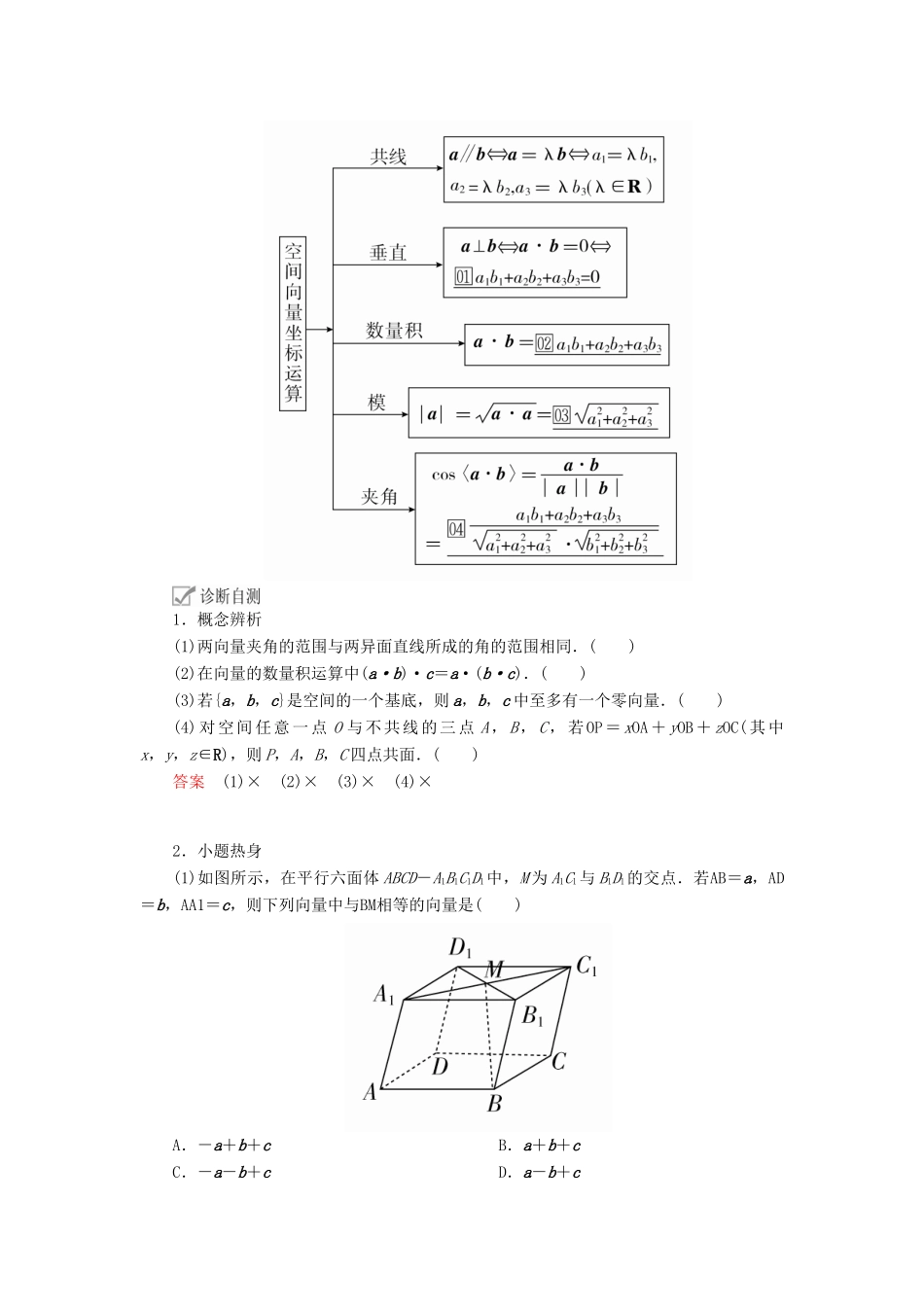
第6讲空间向量及运算[考纲解读]1.了解空间直角坐标系,会用空间直角坐标表示点的位置,了解空间向量的概念,了解空间向量的基本定理及其意义.2.能应用空间两点间的距离公式,掌握空间向量的正交分解及其坐标表示.3.掌握空间向量的线性运算及其坐标表示,掌握空间向量的数量积及其坐标表示,并能运用向量的数量积判断向量的共线与垂直.(重点、难点)[考向预测]从近三年高考情况来看,本讲一直是空间立体几何的基础,一般不单独命题.预测2020年会与多面体相结合进行考查,题型为解答题,解题时利用空间向量法解决问题,试题难度不会太大,属中档题型.1.空间两点间的距离公式、中点公式(1)距离公式①设点A(x1,y1,z1),B(x2,y2,z2),则|AB|=□.②设点P(x,y,z),则与坐标原点O之间的距离为|OP|=□.(2)中点公式设点P(x,y,z)为P1(x1,y1,z1),P2(x2,y2,z2)的中点,则□.2.空间向量的数量积a·b=|a||b|cos〈a,b〉.3.空间向量的坐标运算a=(a1,a2,a3),b=(b1,b2,b3)(a,b均为非零向量):1.概念辨析(1)两向量夹角的范围与两异面直线所成的角的范围相同.()(2)在向量的数量积运算中(a·b)·c=a·(b·c).()(3)若{a,b,c}是空间的一个基底,则a,b,c中至多有一个零向量.()(4)对空间任意一点O与不共线的三点A,B,C,若OP=xOA+yOB+zOC(其中x,y,z∈R),则P,A,B,C四点共面.()答案(1)×(2)×(3)×(4)×2.小题热身(1)如图所示,在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若AB=a,AD=b,AA1=c,则下列向量中与BM相等的向量是()A.-a+b+cB.a+b+cC.-a-b+cD.a-b+c答案A解析由题意,根据向量运算的几何运算法则,BM=BB1+B1M=AA1+(AD-AB)=c+(b-a)=-a+b+c.故选A.(2)若{a,b,c}为空间的一组基底,则下列各项中,能构成基底的一组向量是()A.a,a+b,a-bB.b,a+b,a-bC.c,a+b,a-bD.a+b,a-b,a+2b答案C解析A,B,D中三组向量都是共面向量,不能构成基底,c,a+b,a-b不共面可以构成基底.(3)已知向量a=(2,-3,5),b=,且a∥b,则λ等于________.答案-解析因为a∥b,所以==,所以λ=-.(4)已知a=(1,2,-2),b=(0,2,4),则a,b夹角的余弦值为________.答案-解析cos〈a,b〉==-.题型空间向量的线性运算如图所示,在平行六面体ABCD-A1B1C1D1中,设AA1=a,AB=b,AD=c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:(1)AP;(2)A1N;(3)MP+NC1.解(1) P是C1D1的中点,∴AP=AA1+A1D1+D1P=a+AD+D1C1=a+c+AB=a+c+b.(2) N是BC的中点,∴A1N=A1A+AB+BN=-a+b+BC=-a+b+AD=-a+b+c.(3) M是AA1的中点,∴MP=MA+AP=A1A+AP=-a+a+c+b=a+b+c,又NC1=NC+CC1=BC+AA1=AD+AA1=c+a.∴MP+NC1=+=a+b+c.条件探究在举例说明条件下,若AE=EC,A1F=2FD,试用a,b,c表示EF.解如图,连接AF,则EF=EA+AF.由已知四边形ABCD是平行四边形,故AC=AB+AD=b+c,A1D=A1A+AD=-a+c.又EA=-AC=-(b+c),由已知A1F=2FD,所以AF=AD+DF=AD-FD=AD-A1D=c-(c-a)=(a+2c),所以EF=EA+AF=-(b+c)+(a+2c)=(a-b+c).用已知向量表示某一向量的注意事项(1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键.(2)要正确理解和运用向量加法、减法与数乘运算的几何意义.向量加法的多边形法则对空间向量仍然成立.(3)在立体几何中要灵活应用三角形法则,向量加法的平行四边形法则在空间仍然成立.提醒:灵活运用三角形法则或平行四边形法则,把所求向量用已知基向量表示出来.1.如图所示,在四面体OABC中,OA=a,OB=b,OC=c,D为BC的中点,E为AD的中点,则OE=________(用a,b,c表示).答案a+b+c解析因为D为BC的中点,所以OD=(OB+OC)=(b+c),又因为E为AD的中点,所以OE=(OA+OD)==a+b+c.2.如图所示,已知P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点M在线段PC上,点N在线段PD上,且PM=2MC,PN=ND,若MN=xAB+yAD+zAP,则x+y+z=________.答案-解析MN=PN-PM=PD-PC=(AD-AP)-(P...