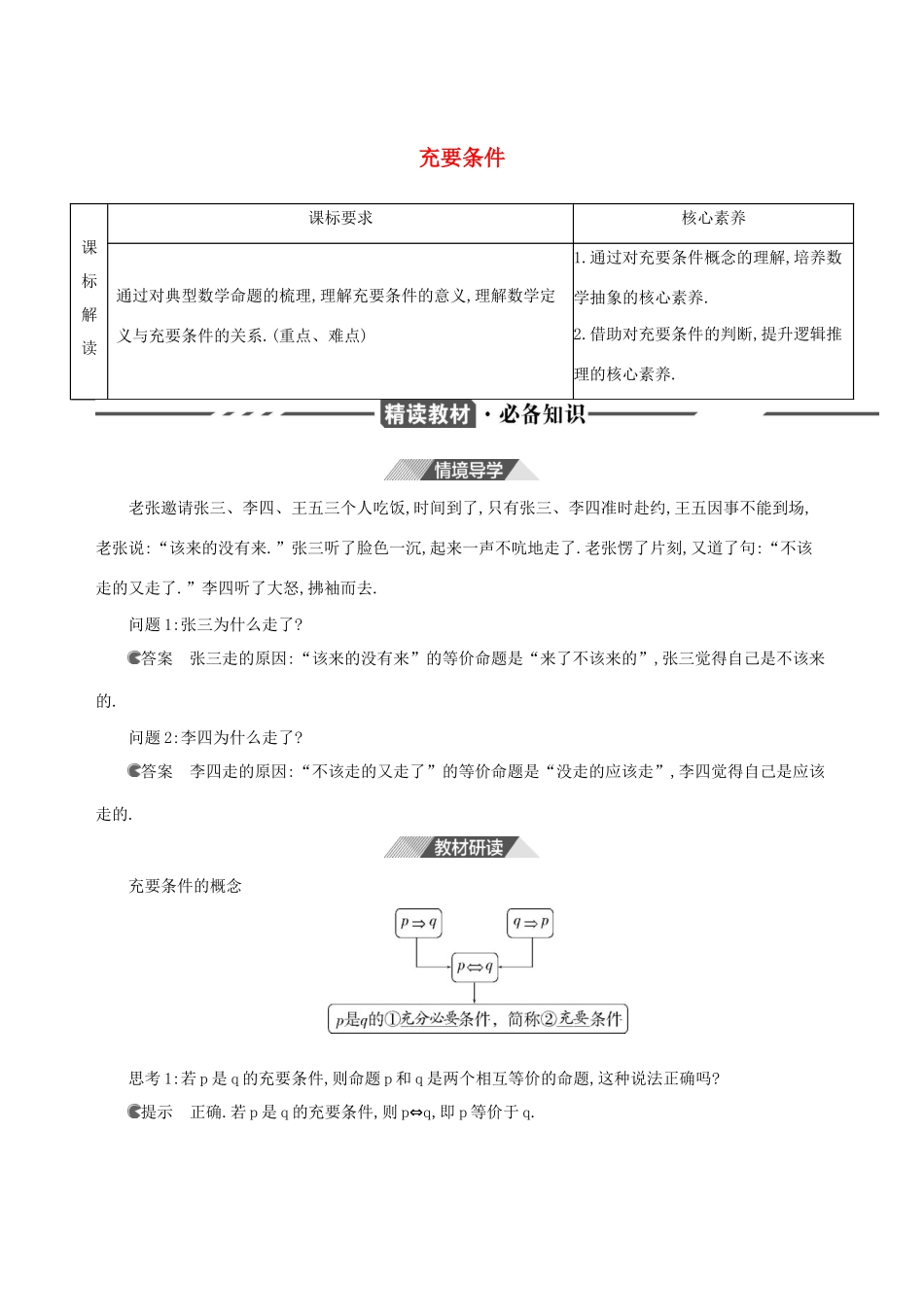
充要条件课标解读课标要求核心素养通过对典型数学命题的梳理,理解充要条件的意义,理解数学定义与充要条件的关系.(重点、难点)1.通过对充要条件概念的理解,培养数学抽象的核心素养.2.借助对充要条件的判断,提升逻辑推理的核心素养.老张邀请张三、李四、王五三个人吃饭,时间到了,只有张三、李四准时赴约,王五因事不能到场,老张说:“该来的没有来.”张三听了脸色一沉,起来一声不吭地走了.老张愣了片刻,又道了句:“不该走的又走了.”李四听了大怒,拂袖而去.问题1:张三为什么走了?答案张三走的原因:“该来的没有来”的等价命题是“来了不该来的”,张三觉得自己是不该来的.问题2:李四为什么走了?答案李四走的原因:“不该走的又走了”的等价命题是“没走的应该走”,李四觉得自己是应该走的.充要条件的概念思考1:若p是q的充要条件,则命题p和q是两个相互等价的命题,这种说法正确吗?提示正确.若p是q的充要条件,则p⇔q,即p等价于q.思考2:记集合A={x|p(x)},B={x|q(x)},若p是q的充分不必要条件,则集合A,B的关系是什么?若p是q的必要不充分条件呢?提示若p是q的充分不必要条件,则A⫋B,若p是q的必要不充分条件,则B⫋A.特别提醒(1)若p⇔q,则称p与q互为充要条件.(2)若p⇒q,但q⇒/p,则称p是q的充分不必要条件.(3)若q⇒p,但p⇒/q,则称p是q的必要不充分条件.(4)若p⇒/q,且q⇒/p,则称p是q的既不充分又不必要条件.探究一充要条件的判断例1(1)(多选)下列选项中,p是q的充要条件的为()A.p:x>0,y<0,q:xy<0B.p:a>b,q:a+c>b+cC.p:x>5,q:x>10D.p:a>b>0,q:❑√a>❑√b(2)设A,B,U是三个集合,且A⊆U,B⊆U,则“x∈(∁UA)∩(∁UB)”是“x∈∁U(A∪B)”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件答案(1)BD(2)C解析(1)对于A选项,p⇒q,但q⇒/p,故p不是q的充要条件;对于B选项,p⇒q,且q⇒p,即p⇔q,故p是q的充要条件;对于C选项,p⇒/q,但q⇒p,故p不是q的充要条件;对于D选项,p⇒q,且q⇒p,故p是q的充要条件.故选BD.(2) (∁UA)∩(∁UB)=∁U(A∪B),∴“x∈(∁UA)∩(∁UB)”是“x∈∁U(A∪B)”的充要条件,故选C.思维突破从命题角度判断p是q的充要条件的原理及方法(1)原理:判断p是q的充要条件主要是判断p⇒q及q⇒p这两个命题是否成立.(2)方法:①若p⇒q成立,则p是q的充分条件,同时q是p的必要条件;②若q⇒p成立,则p是q的必要条件,同时q是p的充分条件;③若二者都成立,则p与q互为充要条件.1.已知a,b是实数,则“a>0且b>0”是“a+b>0且ab>0”的条件;“|ab|=ab”是“ab>0”的条件.答案充要;必要不充分解析因为a>0,b>0,所以a+b>0,ab>0,充分性成立;因为ab>0,所以a与b同号,又a+b>0,所以a>0且b>0,必要性成立.故“a>0且b>0”是“a+b>0且ab>0”的充要条件.当ab=0时,“|ab|=ab”不能推出“ab>0”,而当ab>0时,有|ab|=ab,所以“|ab|=ab”是“ab>0”的必要不充分条件.探究二充要条件的证明例2求证:△ABC是等边三角形的充要条件是a2+b2+c2=ab+ac+bc.(这里a,b,c是△ABC的三边边长)证明必要性: △ABC是等边三角形,∴a=b=c,∴ab+ac+bc=a2+b2+c2,∴必要性成立;充分性:由a2+b2+c2=ab+ac+bc两边同时乘2,得2a2+2b2+2c2=2ab+2ac+2bc,即(a-b)2+(b-c)2+(c-a)2=0,∴a=b=c,∴△ABC是等边三角形.∴充分性成立.综上,△ABC是等边三角形的充要条件是a2+b2+c2=ab+ac=bc.思维突破充要条件的证明策略(1)要证明p是q的充要条件,需要从充分性和必要性两个方向进行,即证明两个命题“若p,则q”为真且“若q,则p”为真.(2)在证明的过程中也可以转化为集合的思想来证明,证明p与q的解集是相同的.提醒:证明时一定要分清充分性与必要性的证明方向.2.求证:一元二次方程ax2+bx+c=0有一个正根和一个负根的充要条件是ac<0.证明必要性:因为方程ax2+bx+c=0有一个正根和一个负根,所以x1x2=ca<0(x1,x2为方程的两根,x1≠x2),所以ac<0.所以必要性成立.充分性:由ac<0,可推得b2-4ac>0,及x1x2=ca<0(x1,x2为方程的两根且x1≠x2),所以方程ax2+bx+c=0有两个不等实根,且两根异号,即方程ax2+bx+c=0有一个正根和一个负根.所以充分性成立.综上可知,一元二次方程ax2+bx+c=0有一个正根和一个负根的充要条件是ac<0.探究三充分条件与必要条件的应用例3已知p:-2≤x≤10,q:1-m≤x≤...