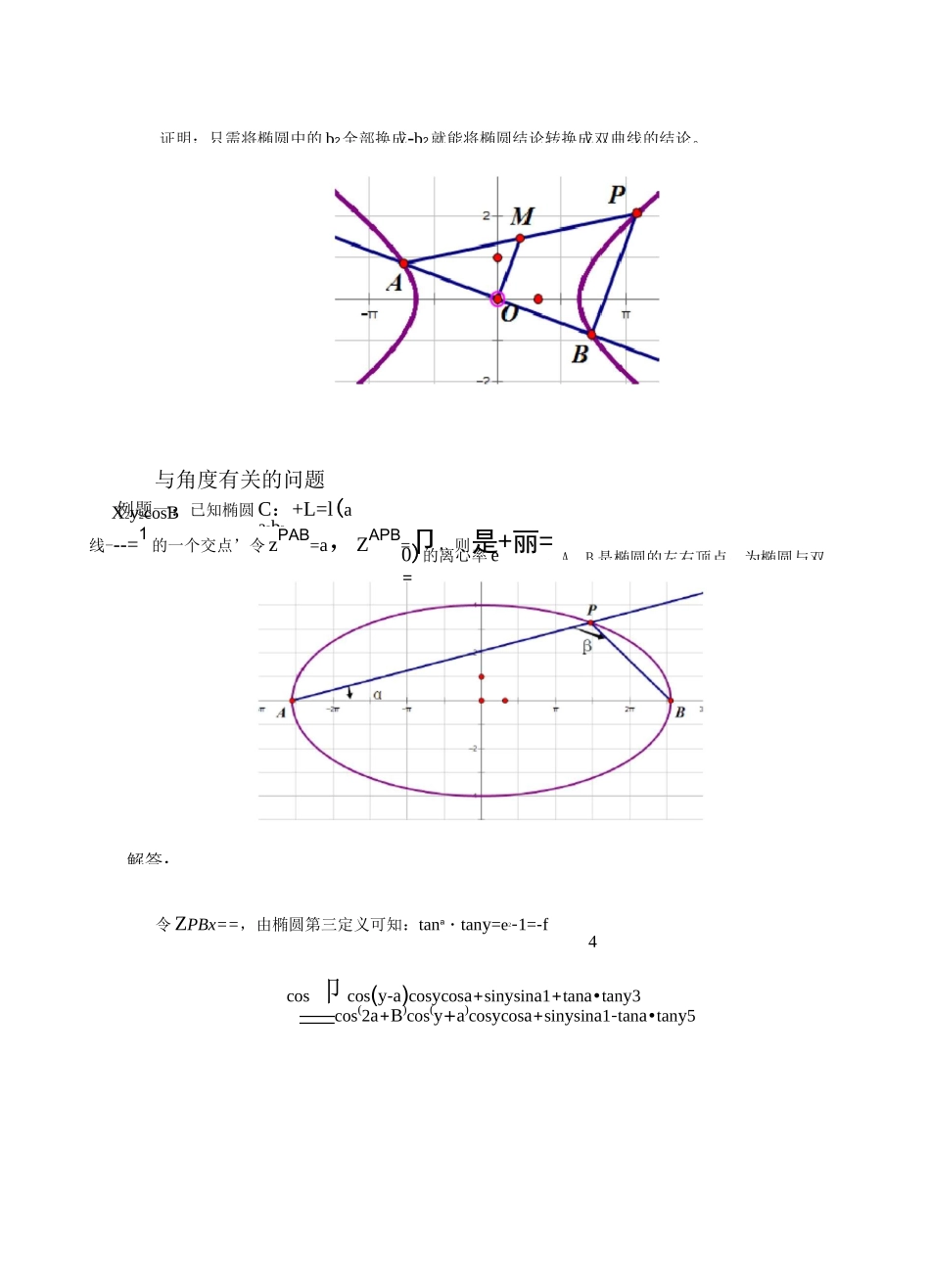
在双曲线C:P厉锥曲线的第三定义及运用椭圆和双曲线的第三定义1.椭圆在椭圆C:—+y=l(ab0)中,A、B是关于原点对称的两点,P是椭圆上异于A、B的一点,a2b2b2若k、k存在,则有:k•k=e2-1=--PAPBPAPBa2证明:构造△PAB的PA边所对的中位线MO,k=k,由点差法结论:k•k=e2-1=--PAMOMOPBa2知此结论成立。2.双曲线y2=1中,A、B是关于原点对称的两点,P是椭圆上异于A、B的一点,若k、kPAPBb2存在,则有:k•k=e2-1=-PAPBa2例题一:已知椭圆C:+L=l(aa2b20)的离心率e=,A、B是椭圆的左右顶点,为椭圆与双与角度有关的问题X2y2cosB线---=1的一个交点’令zPAB=a,ZAPB=卩,则是+丽=令ZPBx==,由椭圆第三定义可知:tana・tany=e2-1=-f4cos卩cos(y-a)cosycosa+sinysina1+tana•tany3——cos(2a+B)cos(y+a)cosycosa+sinysina1-tana•tany5证明:只需将椭圆中的b2全部换成-b2就能将椭圆结论转换成双曲线的结论。解答:点评:其实所谓的双曲线方程只是一个障眼法,并不影响题目的解答。两顶点一动点的模型要很快的联想到第三定义,那么剩下的任务就是把题目中的角转化为两直线的倾斜角,把正余弦转化为正切。题目中的正余弦化正切是三角函数的常见考点^。变式1-1:(石室中学2015级高二下4月18日周末作业)已知双曲线c:x2—y2=2015的左右顶点分别为A、B,P为双曲线右支一点,且ZPAB=4ZAPB,求ZPAB=解答:兀兀令ZpAB=aw0,2,ZPBA=^w0,2,则B=5a,由双曲线的第三定义知:乙2tana•tanB=tana•tan5a=e2一1=1则:1tana=—tan5a=tan一一5a12丿兀~兀na=一—5ana=——点评:连接MB,由椭圆的第三定义可知:与例题1采取同样的思路转化角,但对于正切转换的要求较高。两锐角正切乘积为1即表示sina二cosB,cosa二sinB=两角互余^,则可解出a的值。当然双曲线的题目较于椭圆和抛物线题目考试概率较小,但既然提到了双曲线的第三定义,不妨做一做。三、与均值定理有关的问题例题2:已知A、B是椭圆a2+b|=1Gb0)长轴的两个端点,M、N是椭圆上关于汀由对称的两点,直线AM、BN的斜率分别为件、k2,且k骨匕若即+|kJ的最小值为】,则椭圆的离心率为解答一(第三定义+均值):由题意可作图如下:b2b2k•k=e2—1=—,(而k——k——/..kk=AMBMa2BMBN12a2ikJ-2护i卜ik2卜¥勻——a=2——e弓解答二(特殊值法):这道题由于表达式(k|+|k|)—1非常对称,则可直接猜特殊点求解。|k|=|k|=!时可取最值,12min122连接MB,由椭圆的第三定义可知:k•k=e2一1=AMBM(而k—一k——/..kk=BMBN12a2辽|kJ+2问kJ>4护J•|k2|=4b=1——b=1——e=变式2-2:已知A、B是椭圆—+工—1(aba2b20)长轴的两个端点,若椭圆上存在Q,使ZAQB—#bi^3则M、N分别为短轴的两端点。此时:|k」=|^|=a=2=e=^2。点评:对于常规解法,合理利用M、N的对称关系是解题的关键,这样可以利用椭圆的第三定义将两者斜率的关系联系起来,既构造了“一正”又构造了“二定”利用均值定理“三相等”即可用a、b表示出最值1。当然将|k|qkj前的系数改为不相等的两个数,就不能利用特殊值法猜答案了,但常规解法相同,即变式2-1。变式2-1:已知A、B是椭圆—+苹=l(ab0)长轴的两个端点,M、N是椭圆上关于x轴对称的两a2b2点,直线AM、BN的斜率分别为k、k,且kk去0。若j2|k|+2j2Ik|的最小值为1,则椭圆的离心率121211121为.解答:则椭圆的离心率的取值范围为3+tanaja2tanaa2<2\(取等条件:tana=-,即Q为上顶点)a带入可得:而tanx在—;当椭圆趋于饱满(eT0)解答一(正切+均值):令Q在x轴上方,则直线QA的倾斜角为以0,2,直线QB的倾斜角为PG壬,兀八一「兀]八"fa、tanP-tanaZAQBG—,兀,tanZAQB二tan(P—a丿二2」1+tanptana由椭圆的第三定义:tanatan卩=-,贝ytan卩=-—a2a2tanab2——tanatanp-tana=a2tana1+tanPtanab21——a2兀单增,则Q为上顶点时("QB),所以此时ZAQB>£兀,故eGmax3解答二(极限法):兀当Q趋近于A、B两点时,ZAQBT-(此时Q点所在的椭圆弧趋近于以AB为直径的圆的圆弧,兀ZAQB相当于直径所对的圆周角);当Q在A、B间运动时ZAQB-(Q在以AB为直径的圆内部ZAQB直径所对的圆周角=90°),由椭圆的对称性可猜测当Q为短轴端点时(ZAQB)。max由于:椭圆上存在Q,使ZAQB—,那...