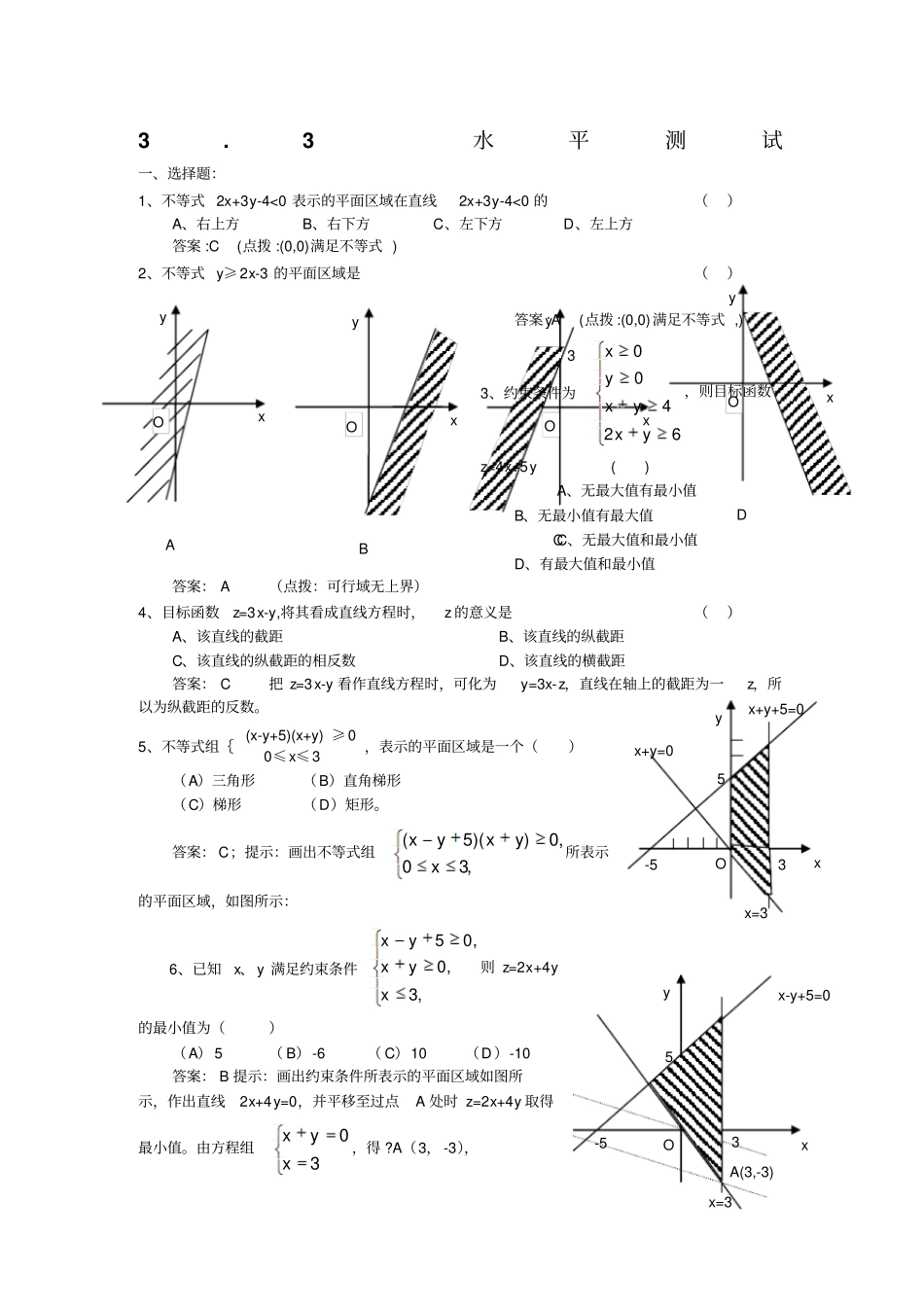
3.3水平测试一、选择题:1、不等式2x+3y-4<0表示的平面区域在直线2x+3y-4<0的()A、右上方B、右下方C、左下方D、左上方答案:C(点拨:(0,0)满足不等式)2、不等式y≥2x-3的平面区域是()答案:A(点拨:(0,0)满足不等式,)3、约束条件为62400yxyxyx,则目标函数z=4x+5y()A、无最大值有最小值B、无最小值有最大值C、无最大值和最小值D、有最大值和最小值答案:A(点拨:可行域无上界)4、目标函数z=3x-y,将其看成直线方程时,z的意义是()A、该直线的截距B、该直线的纵截距C、该直线的纵截距的相反数D、该直线的横截距答案:C把z=3x-y看作直线方程时,可化为y=3x-z,直线在轴上的截距为一z,所以为纵截距的反数。5、不等式组{(x-y+5)(x+y)≥00≤x≤3,表示的平面区域是一个()(A)三角形(B)直角梯形(C)梯形(D)矩形。答案:C;提示:画出不等式组,30,0))(5(xyxyx所表示的平面区域,如图所示:6、已知x、y满足约束条件,3,0,05xyxyx则z=2x+4y的最小值为()(A)5(B)-6(C)10(D)-10答案:B提示:画出约束条件所表示的平面区域如图所示,作出直线2x+4y=0,并平移至过点A处时z=2x+4y取得最小值。由方程组30xyx,得?A(3,-3),xyAOxyBOCxyO3DxyOyxO5-5x+y=0x+y+5=0x=33xyO5-5x-y+5=0x=33A(3,-3)∴zmin=2×3+4×(-3)=-6.二、填空题:7、不等式|3x+2y+k|≤8表示的平面区域必包含(0,0)及(1,1)两点,则k的取值范围是。答案:[-8,3](点拨:将点的坐标代入得3138|5|888||kkkk∴-8k≤3。)8、已知点(3,1)和(-4,6)在直线3x-2y+A=0的两侧,则A的取值范围是.答案:-7
0表示的区域内,则A=。答案:16.提示: ,525|28|a∴|A-6|=10.解得A=16或-4,即p(16,4)或p(-4,4)。又3·(-4)-4-3=-19<0,3×16-4-3=41>0,∴点p(-4,4)不在3x-y-3>0表示的区域内,p(16,4)在3x-y-3>0表示的区域内,∴A=16,三、解答题:13、画出不等式组12002xyyxx表示的平面区域,并求出此不等式的yx21-2-1-1-212y=xy=21x-1x=2整数解。答案:解不等式组组表示的区域如图答所示,其整数解为14、画出不等式组01205012yxyxyx表示的平面区域,并求其面积。答案:取点(2,2)分别代入x-2y+1,x+y-5,2x-y-1,判断正负号知区域如图答所示,由方程组解得A(1,1),B(3,2)C(2,3),|BC|=2,A点到BC的距离D=2311|511|22故其面积S=2323221(平方单位)。15、某车间有一批长250Cm的坯料,现因产品需要,要将它截成长为130Cm和110Cm两种不同条料,生产任务规定:长130Cm条料100根,长110Cm条料150根,问如何开料,使总的耗坯数最小?答案:有两种截料方法。130Cm木料110Cm木料余料第一种方法1110第二种方法0230需要量100150设第一种方法截x根,第二种方法y根,总的耗坏数为z则001502100yxyxxz=x+y如图画出可行域,由图可知在点(100,25)处取得最小值,答:用100根截成130Cm木料和110Cm木料各一根,另用25根截成两根110Cm木料16、医院用两种原料为手术后的病人配制营养食品,甲种原料每10克含5单位蛋白质和10单位铁质,售价3元;乙种原料每10克含7单位蛋白质和4单位铁质,售价2元,若病人每餐至少需要35单位蛋白质和40单位铁质,问应如何配置食品,既满足营养要求,又使费用最省?答案:解:设食品配方中,需甲种原料10x克,乙种原料10y克,所需费用z元。作出可行域如图画直线l0:3x+2y=0,平行移动直线l0到直线l,使l过可行域的某点,...