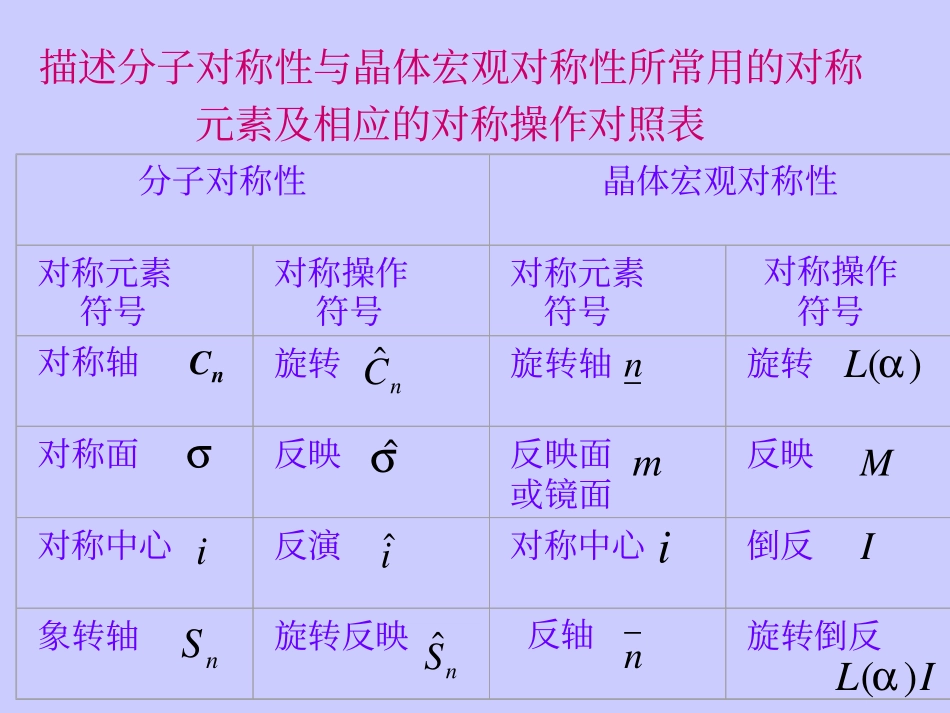
7.2晶体的对称性晶体的对称性有宏观对称性和微观对称系之分。前者是指晶体的外形对称性,后者指晶体微观结构对称性。一.晶体的宏观对称性1.晶体的宏观对称元素和点对称操作晶体的理想外形及其在宏观观察中所表现出的对称性称为宏观对称性,它与有限分子的对称性一样,也具有点对称的性质。对称元素所对应的对称操作群也构成点群。习惯上使用的对称元素和对称操作的符号及名称与讨论分子对称性时不完全相同.描述分子对称性与晶体宏观对称性所常用的对称元素及相应的对称操作对照表分子对称性晶体宏观对称性对称元素符号对称操作符号对称元素符号对称操作符号对称轴Cn旋转旋转轴旋转对称面反映反映面或镜面反映对称中心反演对称中心倒反象转轴旋转反映反轴旋转倒反nCˆn)(αLσσˆmMiiˆiInSnSˆnIL)(α晶体的宏观对称性与有限分子的对称性的根本区别在于:由于晶体中存在的对称性必须与点阵的周期性相一致,因此,晶体的点阵结构使其对称性受到了限制。这种限制体现在下面两个基本原理上。(1)在晶体的空间点阵结构中,任何对称轴(旋转轴、反轴、螺旋轴)都必须与此空间点阵中的一组直线点阵平行,且与一组平面点阵垂直;任何对称面(镜面、滑移面)都必须与此空间点阵中的一组平面点阵平行,且与一组直线点阵垂直。(2)晶体中的对称轴(旋转轴、反轴、螺旋轴)的轴次仅限于=1,2,3,4,6等五种,而不可能存在5及6以上的轴次。证明:设阵点A1,A2,A3,A4···相隔周期为a,有一个n重旋转轴通过点阵点。绕A2点顺时针旋转基转角α得阵点B1,绕A3点逆时针旋转基转角α得阵点B2,B1和B2连线平行于A1和A4连线,B1和B2的间距必为基本周期a的整数倍,设为ma,m为整数,nπα2=aaaaaA1A2A3A4B1B2maaa121coscos2≤−==+mmaaaαα21≤−m(2,1,0,-1,-2)m=3,2,1,0,-1==nπα212π62π42π22π32π即点阵结构中的对称轴的轴次仅限于1,2,3,4,6等五种。63,33=+=+hmi4对称元素记号对称操作等同元素对称中心i倒反I反映面(或镜面)m反映M一重旋转轴1旋转L(360°)二重旋转轴2旋转L(180°)三重旋转轴3旋转L(120°)四重旋转轴4旋转L(90°)六重旋转轴6旋转L(60°)四重反轴旋转倒反L(90°)I受点阵结构的限制,晶体实际可能存在的独立宏观对称元素只有8种4212.晶体的宏观对称元素的组合与32个晶体学点群由上述的8种独立的宏观对称元素按一定的规则(即对称元素至少要通过一个公共点;组合时不能出现5次轴及大于6的对称轴)进行组合,总共有32种组合形式,称为32个晶体学点群。晶体的宏观外形不论形状如何,必属于这32个晶体学点群中的某一个。Cn:C1,C2,C3,C4,C65个Cnv:C2v,C3v,C4v,C6v4个Cnh:C1h=Cs,C2h,C3h,C4h,C6h5个Sn:S2=Ci,(S3与C3h等同),S4,S6=C3i3个Dn:D2,D3,D4,D64个Dnh:D2h,D3h,D4h,D6h4个Dnd:该类点群含有平分面σd,使映转轴次数要扩大一倍,故只有D2d,D3d2个共32个5个高阶群:T、Td、Tu、O、Oh。分子点群与晶体学点群不同之处在于分子不像晶体那样具有点阵结构,分子中允许出现5次轴及大于6的对称轴,所以描述分子对称性的点群就不至32个。2,m,i2/m11109四方中12876两个互相垂直的m或三个互相垂的正交5423或m单斜21无三斜低国际记号熊夫里斯记号序号对称元素点群晶胞类型特征对称元素晶系对称性的高低2223i4o90≠≠≠≠≠γβαcbaβγα≠==≠≠o90cbao90===≠≠γβαcba1cic2cschc22DvD2hD212m2222mm222mmmim,22m,233,m4c4shc44D444m44,4,mi,442o90===≠=γβαcba14227个晶系的划分和32晶体学点群六方晶胞三方2019181716菱面体晶胞151413四方中国际记号熊夫里斯记号序号对称元素点群晶胞类型特征对称元素晶系对称性的高低im,5,24,4vc4dD2hD4mm4m24224mmmm4,4m2,22,4o90===≠=γβαcba43oo90120≠<====γβαcba3cic33Dvc3dD3333m3323i,323,3m3,3im,3,23,3oo12090===≠=γβαcba2m续表:622立方24232221六方中3231302928在立方的体对角线方向高272625国际记号熊夫里斯记号序号对称元素点群晶胞类型特征对称元素晶系对称性的高低mmm6oo12090===≠=γβαcba6chc3hc66Dvc6hD3hD6mm626m226666m6),3(6mim,,626,6m6,6mm4,23),,3(6im,7,26,643o9...