非线性约束优化VIP免费

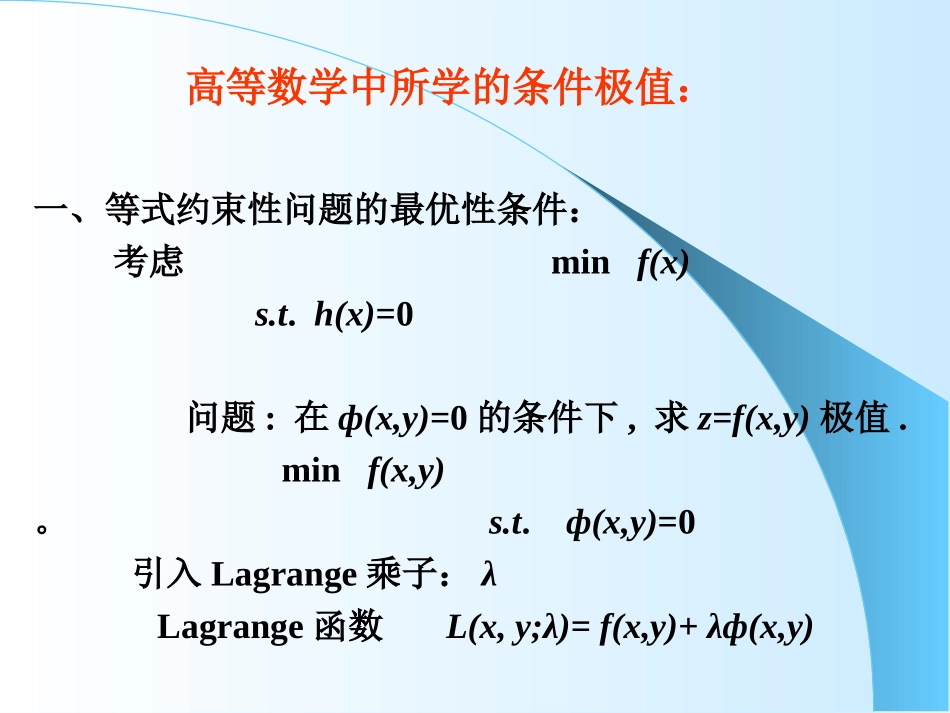
第四章第四章约束最优化方法问题minf(x)s.t.g(x)≤0h(x)=0约束集S={x|g(x)≤0,h(x)=0}(fgh)高等数学中所学的条件极值：一、等式约束性问题的最优性条件：考虑minf(x)s.t.h(x)=0问题:在ф(x,y)=0的条件下,求z=f(x,y)极值.minf(x,y)。s.t.ф(x,y)=0引入Lagrange乘子：λLagrange函数L(x,y;λ)=f(x,y)+λф(x,y)一、等式约束性问题的最优性条件：(续)若(x*,y*)是条件极值，则存在λ*，使fx(x*,y*)+λ*фx(x*,y*)=0fy(x*,y*)+λ*фy(x*,y*)=0Ф(x*,y*)=0推广到多元情况，可得到对于(fh)的情况：minf(x)s.t.hj(x)=0j=1,2,…,l若x*是(fh)的l.opt.,则存在*∈Rl使以及hj(x)=0，j=1,2,…,l***1()()0ljjjfxhx一、等式约束性问题的最优性条件：(续)几何意义是明显的：考虑一个约束的情况：最优性条件即：-f(▽ㄡ)ㄡ▽h(ㄡ)h(x)－▽f(x*)▽h(x*)这里x*---l.opt.f(x*)▽与▽h(x*)共线，而ㄡ非l.opt.▽f(ㄡ)与▽h(ㄡ)不共线。*1(*)(*)hjjjfxhx一等式约束下的拉格朗日乘子算法考虑等式约束问题:令拉格朗日函数:则等式约束下规划问题转化成无约束问题:minL(X,)该问题有极值点的必要条件为:liXhtsXfi,...,2,1,0,0)(..),(minliiiXhXfXL1)()(),(liXhLnjxXhxXfxLiXXilijiijXXj..,2,1,0*)(|,...,2,1,0*)(*)(|**,1***,充分条件:如果且行列式方程:所有根Zj>0(j=1,2,…,n-l)，则X*为局部极小点；反之所有Zj<0，为局部极大点；有正有负非极值点0)*,(XL例题4-1用拉格朗日乘子算法求解:解:令极大点的必要条件:对于得到的三个根。使用充分条件检验如下：02422)(..,)(max2121121xxxxhtsxXf22121112()(2224)LXxxxxx******1*,*1211121*2***2*,*1112**2***11*,*1212(/)24202(/)2041(/)(2224)0xxxLxxxxxxLxxxxLxxxx计算:展开z的(n-l)=(2-1)=1次多项式方程，得00416402162442)(1624)(0),(222),(442),(*12*1*2*11*122**2*1*121**2*1*221**2zzxxXhxxxXhxXLxxxXLxxXL0)168(16)64(2)16)(4(222zz017/121z一个信息处理技术中重要的例子－求最优隶属度函数１）背景介绍－聚类分析２）目标函数－符号说明构造拉日函数：最优化的一阶必要条件为代回上式进入到约束条件：得所以2111(,),..1,1~cncmijijijiijJUVudstujn211()(1)ccmijijijiiLudu121/(1)21(1)0;[()]0;[]cmmijijijijiijijLLumuduumd1]1[)(]1[)(11)1/(12)1/(1)1/(12)1/(11cicimijmmijmciijdmdmu2/(2)11[]ijcijmlljuddFCM的中心迭代过程2)2)不等式约束问题的不等式约束问题的Khun-TuckerKhun-Tucker条件：条件：考虑问题minf(x)s.t.gi(x)0i=1,2,…,m设x*∈S={x|gi(x)0i=1,2,…,m},并令I={i|gi(x*)=0，i=1,2,…,m}称I为x*点处的起作用集（紧约束集）。如果x*是l.opt.,对每一个约束函数来说，只有当它是起作用约束时，才产生影响，如：g2(x)=0x*g1(x)=0g1(x*)=0,g1为起作用约束，约束集已知时回归到含等式优化问题问题:事先并不知道约束集＝？定理（任意情况的最优性必要条件）：（K-T条件）问题(fg),设Ｄ={x|gi(x)0，},x*∈Ｄ,I为x*点处的起作用集，设f,gi(x),iI∈在x*点可微，gi(x),iI在x*点连续。向量组{g▽i(x*),iI∈}线性无关。构造拉日函数：如果x*----l.opt.那么，u*i≥0,使得１）驻点条件：２）互补条件：３）非负条件：４）不等式约束：５）等式约束：说明：１）如果是max问题等，要改变叙述。２）在一定条件下上面叙述变成充要条件。***11()()()0mliijjijfxgXhX*01,2,,iuim()01,2,,igximliXhi,...,2,1,0*)(ljxhmij~1,0)(;~1...