综合理论力学VIP免费

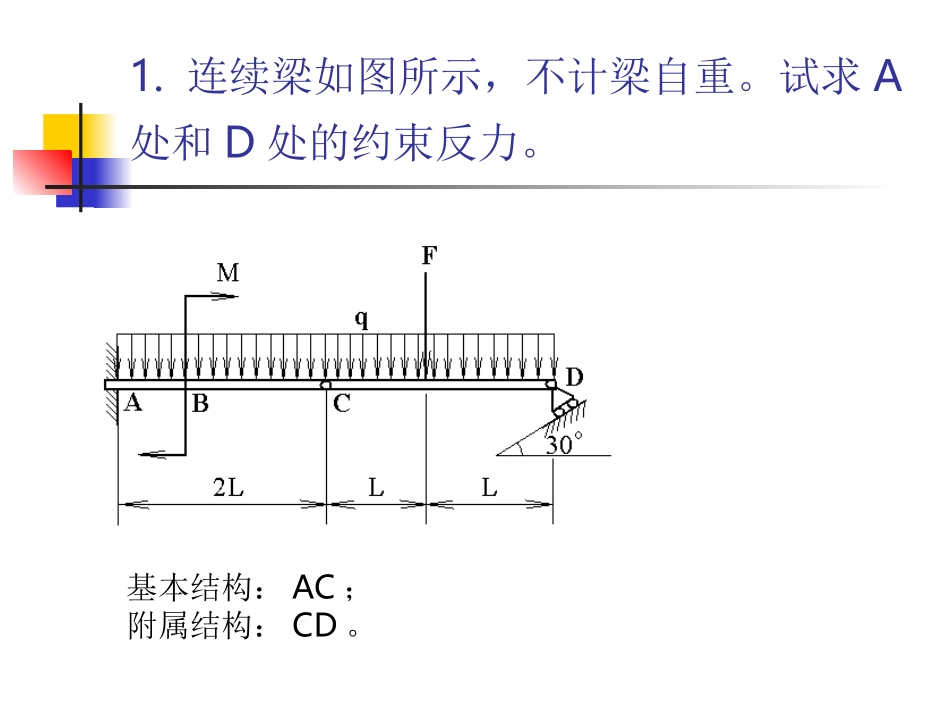
理论力学复习课静力学复习题1.连续梁如图所示，不计梁自重。试求A处和D处的约束反力。基本结构：AC；附属结构：CD。对CD:0CMDF0xFCxF0yFCyF对AC：0xFAxF0yFAyFAM0AM对CD:0CMDF对整体：0xFAxF0yFAyF0AMAM2.图示组合梁，不计梁自重。求支座A，B，D的约束力和铰链C处所受的力。基本结构：AC；附属结构：CD。3．结构尺寸及载荷如图所示。杆重不计。求支座、处约束反力以及拉杆所受的力。DE为二力杆。4.构架的尺寸及载荷如图所示，杆重不计。试求支座、处约束反力。CD为二力杆；AD为基本结构，BC为附属结构。5.图示结构，不计所有杆件自重，求和两处的约束反力。BCD为二力杆；AB为基本结构，ED为附属结构。6.图示桁架结构如图所示。(1)判断哪些杆件是零杆；(2)用节点法求杆1、2、7、8的内力；(3)用截面法求杆3、6、10的内力。对整体：对节点B：对节点A：60FMD30FMG100FFx7.图示桁架结构，求：（1）B、E支座处的约束反力；（2）1，2，3杆的内力。（1）求约束反力。（2）截面法求杆的内力。03F20FMH10FFy运动学复习题1.图示曲柄滑道机构，曲柄长OA=100mm，并绕O轴转动。在某瞬时，其角速度1rad/s，角加速度1rad/s2，求此时（1）导杆上C点的速度；（2）导杆上C点的加速度；（3）滑块A在滑道中的相对加速度。动点：OA杆上A点（滑块A）动系：与BC固结。aervvvavOA2naaOAaaOAaeraaanaaeraaaa2．半径为R的半圆形凸轮以等速沿水平线向右运动，带动从动杆沿铅直方向上升，如图所示。求杆相对于凸轮的速度和加速度。取杆上A为动点，动系与凸轮固结。reavvv0vve003330tantanvvvvea0033230coscosvvvver0eaRvRvarnr34202reaaaanarraaa3.图示铰接四连杆机构中，求CD杆的速度和加速度。4.已知OA杆的角速度（匀速转动）。求B点的速度、加速度以及AB杆的角速度和角加速度。2m/sm/s2.0100OAvA2rad/srad/s12APvAAB?BPvABBBAABaaaBAnBAABaaaam/s2020OAaanAA22m/s4ABaABnBA把加速度矢量方程向X轴投影，得)(m/s67.545cos2BnBABaaa把加速度矢量方程向Y轴投影，得2m/s1645sinBABAABaaaa2rad/s16ABaBAAB5.求该时刻（1）杆AB的角速度和角加速度；（2）B点的速度和加速度。BAnBAABaaaaBAABaaaAABvAP?BPvABB2nBAABaAB6．在图示曲柄连杆机构中，滑块的切向和法向加速度。rOAvooAooAABrrACv212rrBCvooABB2421ooBBrrBOv221BAABaaaBAnBAAnABnBaaaaaarOAaOonA22raoArrABaooABnBA2222332)2(rrBOaooBnB221222动力学复习题1．轮子相对于质心O的回转半径为。求重物A的加速度。解法一：对轮子的质心用刚体的平面运动的微分方程。对重物A，有：Tgmam11对轮子的质心用刚体的平面运动的微分方程：xOxFmafOxFTamam22yOyFmagmNamOy220)(FMJOORFrTmf22rRaNFTaf,,,（1）（2）（3）（4）解法二：对轮子的速度瞬心O1点用动量矩定理。对重物A，有：Tgmam11对轮，对轮子与地面的接触点O1运用动量矩定理：)(1RrTJO22221RmmJOrRa（1）（2）联立（1）、（2）式，解得：)()()(2222121RmRrmRrgma2均质杆AB和OD在D处垂直地固结成T字形，置于铅垂平面内，且D为AB中点。AB和OD质量均为m，长度均为L。初始时系统静止，OD杆铅垂。现在OD杆上作用一逆时针常力偶mgLM20，使系统发生转动。求当OD杆转至水平位置时：（1）O...