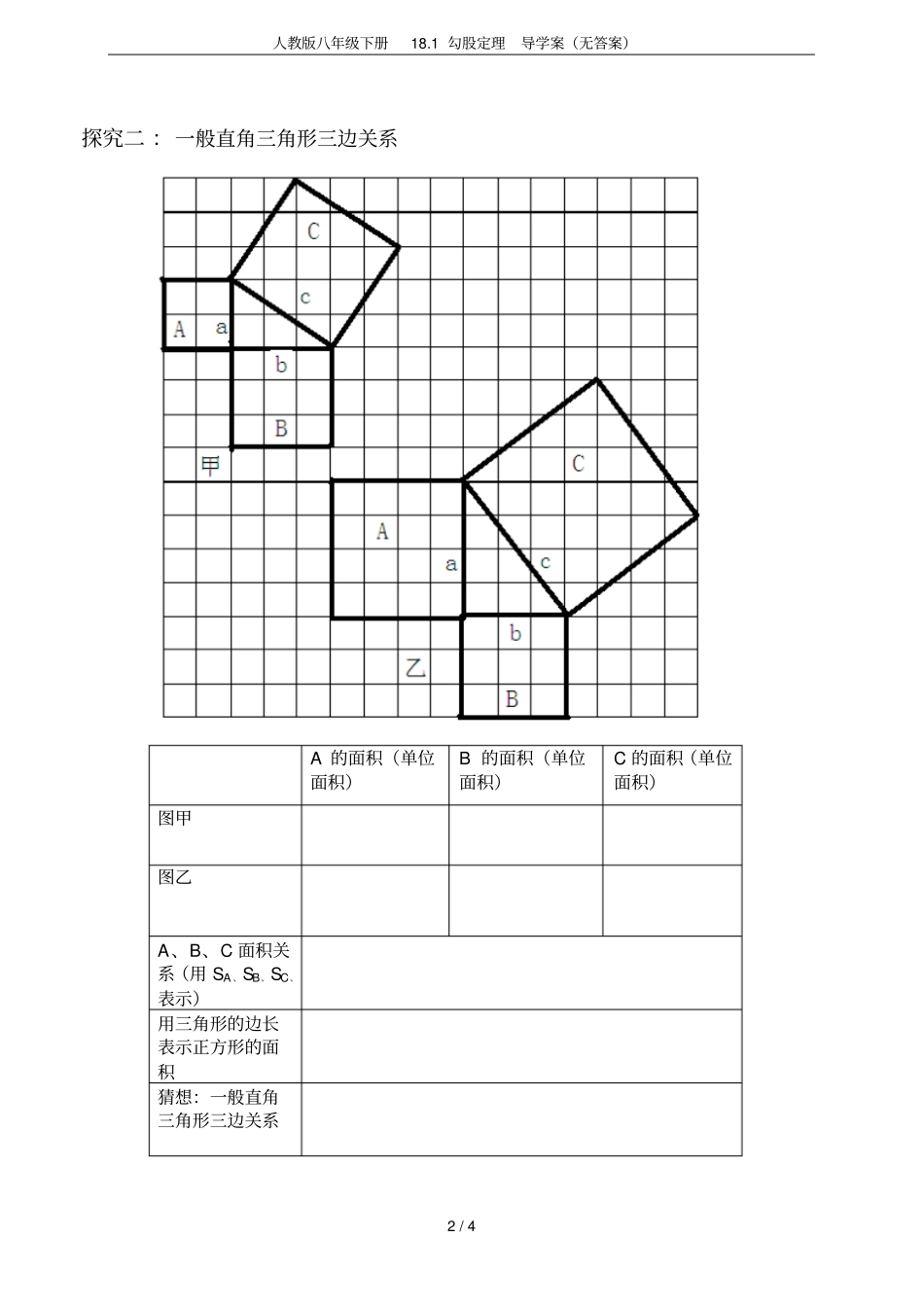
人教版八年级下册18.1勾股定理导学案(无答案)1/418.1勾股定理导学案学习目标:1、了解勾股定理的文化背景,体会勾股定理的探索过程,明确直角三角形两直角边和斜边的关系。2、体会用勾股定理解决简单问题。一、自主探究(享受探究的快乐)探究一:让我们一起探究:等腰直角三角形三边关系A的面积(单位面积)B的面积(单位面积)C的面积(单位面积)图甲图乙A、B、C面积关系(用SA、SB、SC、表示)用三角形的边长表示正方形的面积猜想:等腰直角三角形三边关系人教版八年级下册18.1勾股定理导学案(无答案)2/4探究二:一般直角三角形三边关系A的面积(单位面积)B的面积(单位面积)C的面积(单位面积)图甲图乙A、B、C面积关系(用SA、SB、SC、表示)用三角形的边长表示正方形的面积猜想:一般直角三角形三边关系人教版八年级下册18.1勾股定理导学案(无答案)3/4探究三:你会用四个全等的直角三角形拼成那些图形?组内交流:通过自主探究,你学习了哪些知识?运用了哪些数学思想方法?二、尝试应用(试一试,你一定行!)1、直角三角形的斜边长是13,一直角边长是12,则另一直角边长是.2、在△ABC中,∠C=90°,若AB=4,BC=3,则().A.5B.7C.25D.5或73、三角形的三边分别是下列各组数,是直角三角形三边的是().A、1,2,3B、3,3,4C、9,12,15D、6,10,114、若直角三角形的两直角边分别为6、8,则此直角三角形的周长是().A.14B.18C.16D.24人教版八年级下册18.1勾股定理导学案(无答案)4/45、直角三角形的两条边长分别是3cm,4cm,试求第三边的长。组内交流:通过对3、5题的解决,对你有什么启示?三、补偿提高(更上一层楼)1、斜边长为13,一直角边长为12的直角三角形的面积为。2、直角三角形的面积为6cm2,一直角边为3cm,则斜边长为。3、在Rt△ABC中,∠C=90°,若a:b=3:4,c=10,则a=,b=。4、已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。四、反思提升:(畅所欲言:谈谈本节课所学得知识⋯⋯)1、本节课我们经历了怎样的探究过程?2、本节课我们学到了什么知识和方法?3、有什么感想和疑惑?