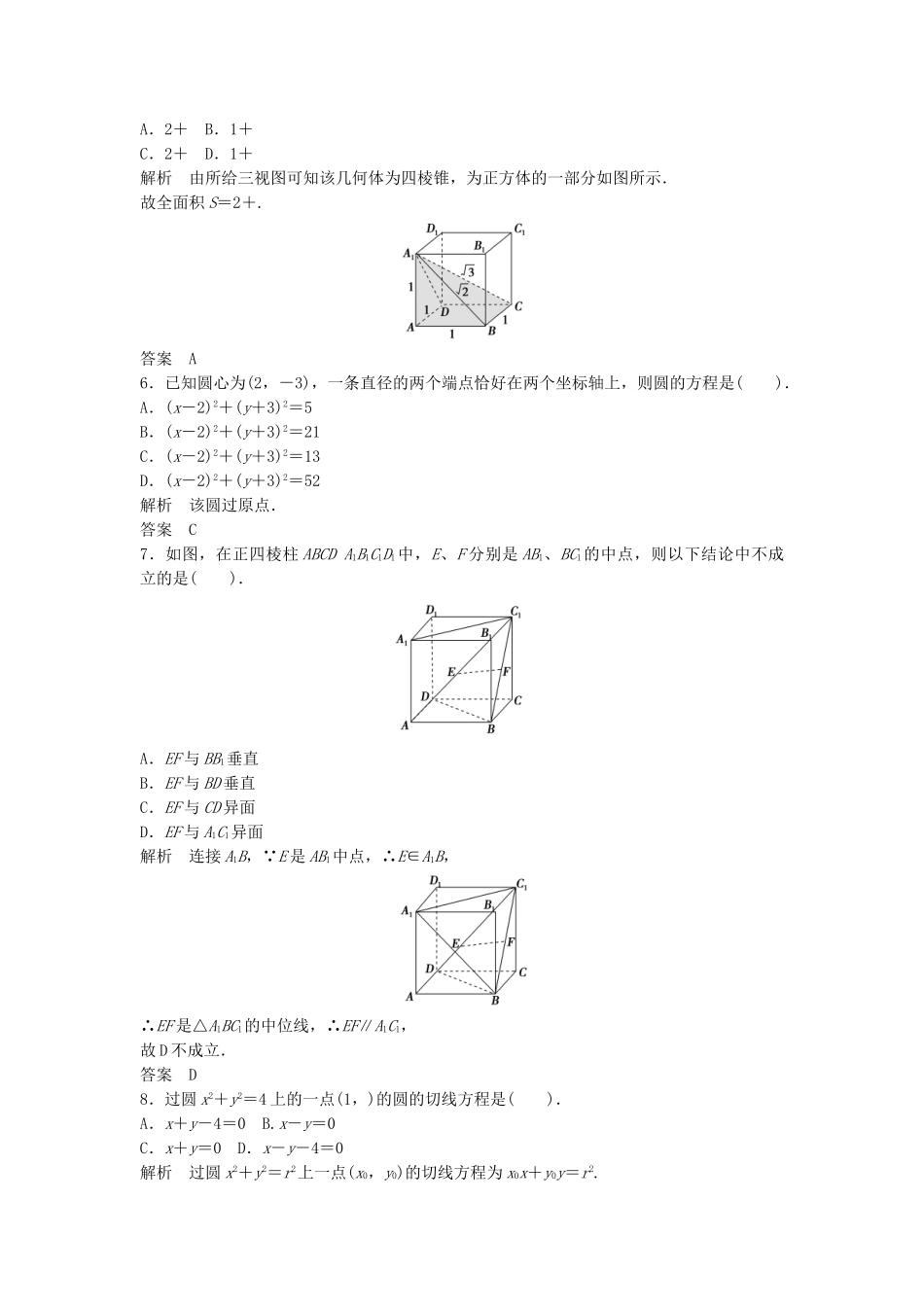
模块检测(时间:120分钟满分:150分)一、选择题(本题共10小题,每小题5分,共50分)1.在某几何体的三视图中,主视图、左视图、俯视图是三个全等的圆,圆的半径为R,则这个几何体的体积是().A.πR3B.πR3C.πR3D.πR3解析由三视图知该几何体为半径为R的球,知V=πR3.答案D2.已知水平放置的△ABC是按斜二测画法得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=,那么△ABC是一个().A.等边三角形B.直角三角形C.等腰三角形D.三边互不相等的三角形答案A3.已知直线m、n与平面α、β给出下列三个语句:①若m∥α,n∥α,则m∥n;②若m∥α,n⊥α,则n⊥m;③若m⊥α,m∥β,则α⊥β.其中正确的个数是().A.0B.1C.2D.3解析①中m与n可能相交,也可能异面.∴①错误.答案C4.已知两点A(-1,3),B(3,1),当C在坐标轴上,若∠ACB=90°,则这样的点C的个数为().A.1B.2C.3D.4解析由题意,点C应该为以AB为直径的圆与坐标轴的交点,以AB为直径的方程是(x+1)(x-3)+(y-3)(y-1)=0,令x=0,解得y=0或4;令y=0,解得x=0或2.所以该圆与坐标轴的交点有三个:(0,0),(0,4),(2,0).答案C5.三视图如图所示的几何体的全面积是().A.2+B.1+C.2+D.1+解析由所给三视图可知该几何体为四棱锥,为正方体的一部分如图所示.故全面积S=2+.答案A6.已知圆心为(2,-3),一条直径的两个端点恰好在两个坐标轴上,则圆的方程是().A.(x-2)2+(y+3)2=5B.(x-2)2+(y+3)2=21C.(x-2)2+(y+3)2=13D.(x-2)2+(y+3)2=52解析该圆过原点.答案C7.如图,在正四棱柱ABCDA1B1C1D1中,E、F分别是AB1、BC1的中点,则以下结论中不成立的是().A.EF与BB1垂直B.EF与BD垂直C.EF与CD异面D.EF与A1C1异面解析连接A1B, E是AB1中点,∴E∈A1B,∴EF是△A1BC1的中位线,∴EF∥A1C1,故D不成立.答案D8.过圆x2+y2=4上的一点(1,)的圆的切线方程是().A.x+y-4=0B.x-y=0C.x+y=0D.x-y-4=0解析过圆x2+y2=r2上一点(x0,y0)的切线方程为x0x+y0y=r2.答案A9.若x、y满足x2+y2-2x+4y-20=0,则x2+y2的最小值是().A.-5B.5-C.30-10D.无法确定解析配方得(x-1)2+(y+2)2=25,圆心坐标为(1,-2),半径r=5,所以的最小值为半径减去原点到圆心的距离,即5-,故可求x2+y2的最小值为30-10.答案C10.若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是().A.(x-3)2+2=1B.(x-2)2+(y-1)2=1C.(x-1)2+(y-3)2=1D.2+(y-1)2=1解析设圆心为(a,b),由题意知,b=r=1,1=,又 a>0,∴a=2.∴圆的标准方程为(x-2)2+(y-1)2=1.答案B二、填空题(本题共5小题,每小题5分,共25分)11.已知l1:2x+my+1=0与l2:y=3x-1,若两直线平行,则m的值为________.答案-12.如图所示,已知AB⊥平面BCD,BC⊥CD,则图中互相垂直的平面有__________________________.答案平面ABD⊥平面BCD,平面ABC⊥平面BCD,平面ABC⊥平面ACD.13.已知直线5x+12y+a=0与圆x2-2x+y2=0相切,则a的值为________.解析=1,解得a=8或-18.答案8或-1814.过点P(1,)的直线l将圆C:(x-2)2+y2=4分成两段弧,当劣弧所对的圆心角最小时,直线l的斜率k为________.解析当直线与PC垂直时,劣弧所对的圆心角最小,故直线的斜率为.答案15.一个三棱锥SABC的三条侧棱SA、SB、SC两两互相垂直,且长度分别为1,,3,已知该三棱锥的四个顶点都在同一个球面上,则这个球的表面积为________.解析以三棱锥的三条侧棱SA、SB、SC为棱长构造长方体,则长方体的体对角线即为球的直径,长为4,∴球半径为2,S球=4πR2=16π.答案16π三、解答题(本题共6小题,共75分)16.(12分)已知△ABC中,∠ACB=90°,SA⊥平面ABC,AD⊥SC.求证:AD⊥平面SBC.证明 ∠ACB=90°,∴BC⊥AC.又SA⊥平面ABC,BC平面ABC,∴SA⊥BC.又SA∩AC=A,∴BC⊥平面SAC, AD平面SAC,∴BC⊥AD.又SC⊥AD,SC∩BC=C,SC平面SBC,BC平面SBC,∴AD⊥平面SBC.17.(12分)已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x-y-5=0,AC边上的高线BH所...